iO（Indistinguishability Obfuscation,，不可區(qū)分混淆）是密碼學(xué)中黑科技一樣的存在,，但很多人認(rèn)為它并不存在,。最近,，一些研究人員提出了新的 iO 協(xié)議,。
2018 年,，加州大學(xué)洛杉磯分校博士生 Aayush Jain 前往日本演講,，介紹他和同事正在開發(fā)的一款強大的加密工具。在他陳述團(tuán)隊在 iO 方面的努力時,，有觀眾提問：「我認(rèn)為 iO 不存在,。」
當(dāng)時,，這種看法較為普遍,。如果 iO 確實存在，它不僅可以隱藏數(shù)據(jù)集合,，還可以隱藏計算機程序的內(nèi)部工作機制,，創(chuàng)造出強大的加密工具。哈佛大學(xué)計算機科學(xué)教授 Boaz Barak 表示,，這是「掌控一切的密碼學(xué)原語」,，而這種力量的強大讓人們懷疑 iO 是否真的存在。
2013 年,，計算機科學(xué)家 Sanjam Garg,、Amit Sahai 等人首次提出 iO 的候選版本，后來其他研究者找出了對其安全性進(jìn)行攻擊的方法,?！刚l將贏得勝利， the makers or the breakers,？」
加州大學(xué)伯克利分校西蒙斯計算理論研究所負(fù)責(zé)人 Shafi Goldwasser 表示：「當(dāng)時很多人對此很狂熱,，他們相信 iO 的存在，并堅持研究,。但后來這些人越來越少了,。」
而近期,，Aayush Jain 與華盛頓大學(xué)副教授 Huijia Lin,、Jain 的導(dǎo)師 Amit Sahai 合作的一項研究為 maker 站臺。這篇于 8 月 18 日線上發(fā)布的論文首次展示了,，如何僅使用「標(biāo)準(zhǔn)」安全假設(shè)來構(gòu)建 iO,。
論文鏈接：https://eprint.iacr.org/2020/1003.pdf
加州大學(xué)伯克利分校博士生,、論文一作 Aayush Jain
所有的加密協(xié)議都依賴于一些假設(shè)，譬如著名的 RSA 算法基于一條被普遍認(rèn)同的觀點：標(biāo)準(zhǔn)計算機無法對兩個大素數(shù)的乘積進(jìn)行因式分解,。加密協(xié)議的安全性和其假設(shè)有關(guān),，之前的 iO 基于未經(jīng)測試、最終被證明不可靠的假設(shè),。而最新的協(xié)議依賴于經(jīng)過廣泛使用和研究的安全假設(shè)。
盡管這一協(xié)議距離現(xiàn)實部署還很遙遠(yuǎn),，但它從理論角度提供了一種即時構(gòu)建多個加密工具的方式,，而這在之前是不可能的。例如,，它允許創(chuàng)建「可否認(rèn)」加密和「函數(shù)」加密,。
以色列理工學(xué)院教授 Yuval Ishai 表示：「現(xiàn)在應(yīng)該不會有人懷疑 iO 的存在了?！?/p>
iO：密碼學(xué)「皇冠上的明珠」
數(shù)十年來,，計算機科學(xué)家一直在思考是否存在安全、全面的方式來實現(xiàn)計算機程序混淆,，使人們能夠在不了解其內(nèi)部秘密的情況下使用它們,。程序混淆可以支持大量實際應(yīng)用，如使用混淆程序在銀行或電子郵件賬戶中向他人委派任務(wù),，而無需擔(dān)心別人濫用該程序或讀取你的賬戶密碼,。
但截至目前，所有構(gòu)建現(xiàn)實混淆器的嘗試都失敗了,。2001 年,，理論層面也出現(xiàn)了壞消息：最強大的混淆形式「黑盒混淆」是難以實現(xiàn)的。（黑盒混淆即攻擊者無法了解程序內(nèi)部,，只能看到程序的使用及其輸出,。）Boaz Barak、Amit Sahai 以及其他五位研究者證明,，一些程序自己揭示了內(nèi)部秘密,，它們無法實現(xiàn)完全混淆。
不過,，這些程序是專門創(chuàng)建來抵抗混淆的,，與現(xiàn)實程序沒有太多相似之處。因此,，計算機科學(xué)家希望存在另外一些混淆,，它足夠弱因此是可行的，又足夠強能夠隱藏人們真正關(guān)心的秘密,。證明黑盒混淆不可能實現(xiàn)的研究者在論文中提出了一個可能的替代方案：iO,。
乍一看,，iO 并不是特別有用的概念。它不要求隱藏程序的秘密,，只要求程序足夠混淆,，比如你有兩個可執(zhí)行相同任務(wù)的不同程序，你無法區(qū)分哪個是混淆版本,，哪個是原版,。
Aayush Jain 導(dǎo)師、UCLA 教授 Amit Sahai,，也是 iO 候選版本的提出者之一,。
但是，iO 實際上要強大得多,。例如,，假設(shè)你有一個程序，可以執(zhí)行一些與銀行賬戶相關(guān)的任務(wù),，但是它包含未加密密碼,，因此易受攻擊。但是,，只要有一個執(zhí)行同樣任務(wù)但能夠隱藏密碼的程序,，不可區(qū)分混淆器就可以成功地 mask 密碼。
近年來,，計算機科學(xué)家證明 iO 可以作為幾乎所有加密協(xié)議的基礎(chǔ)（除了黑盒混淆）,，包括經(jīng)典的加密任務(wù)（如公鑰加密）和新興任務(wù)（如全同態(tài)加密）。它還涵蓋無人知道如何構(gòu)建的加密協(xié)議,，如可否認(rèn)加密和函數(shù)加密,。
康奈爾大學(xué)教授 Rafael Pass 表示：「這是皇冠上的明珠。一旦實現(xiàn),，我們可以獲得一切,。」
2013 年,，Sanjam Garg,、Amit Sahai 等人提出 iO 候選版本，將一個程序分割成多個「拼圖塊」,，然后使用多重線性映射混淆單個「拼圖塊」,。把所有拼圖塊拼在一起后，所有混淆互相抵消,，程序運轉(zhuǎn)如常,，但是每個單獨的「拼圖塊」看起來是無意義的。當(dāng)時,，這一研究結(jié)果被視為一大突破,，并引發(fā)了后續(xù)大量相關(guān)論文,。然而幾年后，其他研究者發(fā)現(xiàn)多重線性映射并不安全,。之后又出現(xiàn)了其他 iO 候選版本,，但也都被攻破。
當(dāng)時,，很多人擔(dān)心 iO 可能只是個無法實現(xiàn)的奇跡,。
少即是多
2016 年，Huijia Lin 開始研究能否通過簡單地減少多項式計算,，來解決多重線性映射的缺陷,。多重線性映射本質(zhì)上是多項式計算的加密方式。Jain 表示：「這些映射類似于多項式計算器,，并與包含變量值的 secret locker 相連接?！箼C器接受用戶輸入的多項式,，用戶可以查看最終 locker，以了解隱藏值能否使多項式的值為 0,。
為了確保該方案的安全性,，用戶不應(yīng)了解有關(guān)其他 locker 的信息或者過程中生成的任何數(shù)字。Sahai 表示：「我們希望這是真的,，」但是,，在研究人員提出的所有候選多重線性映射中，打開最終 locker 的過程中總是泄露出本該隱藏的計算信息,。
華盛頓大學(xué)副教授,、該研究第二作者 Huijia Lin。
研究人員提出的的多重線性映射均存在安全漏洞,，Lin 想知道是否有一種方法,，不必計算那么多不同種類的多項式也能構(gòu)建 iO（因此更容易被安全地構(gòu)建）。
四年前,，Lin 發(fā)現(xiàn)了僅使用某些類型的多重線性映射構(gòu)建 iO 的方法,，這些映射計算「階數(shù)（degree）」為 30 或者更小的多項式（這意味著每個項是最多 30 個變量的乘積）。接下來的幾年中,，Lin,、Sahai 和其他研究者致力于如何將階數(shù)降得更低。直到能夠使用三階多重線性映射構(gòu)建 iO,。
理論上,，這似乎是一個巨大的進(jìn)步。但它仍存在一個問題：從安全的角度講,，三階實際上與任意階多項式處理機器一樣差,。
研究者了解如何安全構(gòu)建的唯一多重線性映射是二階或者更低階的多項式處理機器,。Lin 與 Jain、Sahai 一道,，試圖找出用二階多重線性映射構(gòu)建 iO 的方法,，他們在這個問題上掙扎了很久。
盡管探究過程充滿艱辛,，但最終他們提出了一種新的想法：由于 iO 需要三階映射,，而計算機科學(xué)家只能安全構(gòu)建二階映射，那么二者是否存在折中方案,？比如 2.5 階映射,？
研究者設(shè)想了一個系統(tǒng)，其中某些 locker 具備清晰的窗口,，因此用戶能夠查看其中包含的值,。這使得機器不需要保護(hù)太多的隱藏信息。為了在高階多重線性映射的能力與二階映射的安全性之間取得平衡,，機器可以使用高于二階的多項式進(jìn)行計算,，但是有一個限制：隱藏變量的多項式必須為二階。研究者稱他們試圖不隱藏太多信息,，并證明能夠安全構(gòu)建這類混合 locker 系統(tǒng),。
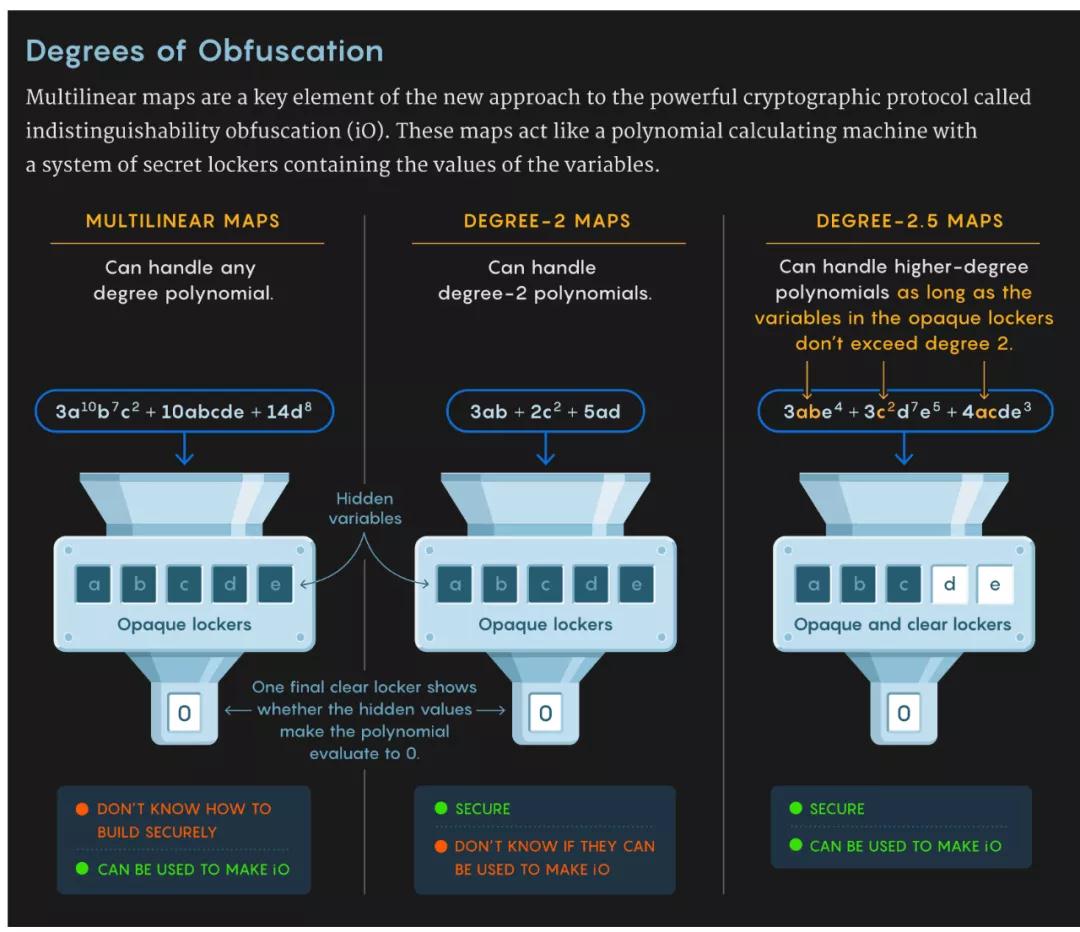
要將這些功效較弱的多重線性映射轉(zhuǎn)換為 iO，還需要最后一個要素：一種新型的偽隨機數(shù)生成器,。它可以將一串隨機位擴(kuò)展為更長的字符串,，并且仍具有隨機性。
該研究的最終成果是能夠避免多重線性映射安全弱點的 iO 協(xié)議,。
該方案的安全性基于在在其他加密環(huán)境中被廣泛使用的四個數(shù)學(xué)假設(shè),，這些假設(shè)歷史悠久，研究時間最短的假設(shè)相關(guān)問題都可以追溯到 20 世紀(jì) 50 年代,。
只可能有一種情況會打破該研究提出的新 iO 協(xié)議,，那就是全功率量子計算機。四個假設(shè)之一易受量子攻擊,，但最近的一些研究已經(jīng)提供了通往 iO 的另一種潛在途徑,，保證它即使受到量子攻擊也是安全的，不過它所依賴的假設(shè)沒有那么堅固,。有研究者表示,，在未來的研究中可以將兩種方法結(jié)合起來，創(chuàng)造出既基于標(biāo)準(zhǔn)安全假設(shè)又能抵擋量子攻擊的 iO 版本,。
這可能會吸引新的研究人員加入,。當(dāng)理論上存在可行性時，那么就會有更多人愿意加入研究團(tuán)隊。毫無疑問,，在該協(xié)議（或其變體）用于實際應(yīng)用之前,，計算機科學(xué)領(lǐng)域仍然有很多事要做。