本文將采用一種與傳統(tǒng)方法不同的方式介紹連續(xù)時間Σ-Δ (CTSD) ADC技術,以便信號鏈設計人員了解這種簡單易用的新型精密ADC技術,將其想像成一個連接了某些已知組件的簡單系統(tǒng)。在第1部分,我們主要介紹了現(xiàn)有信號鏈設計的關鍵挑戰(zhàn),利用精密CTSD ADC,在實現(xiàn)高精度的同時還可保持連續(xù)時間信號完整性,從而可以顯著簡化這些設計。現(xiàn)在的問題是CTSD架構背后是什么使其能夠實現(xiàn)這些優(yōu)勢?
采用傳統(tǒng)方法解釋CTSD技術概念時,都是先理解離散時間∑-? (DTSD)調(diào)制器環(huán)路的基本原理,然后用等效的連續(xù)時間元件來替換離散時間環(huán)路元件。雖然通過這種方法可以深入了解∑-?功能,但我們的目標是更直觀地了解精密CTSD ADC內(nèi)在優(yōu)勢的背后原因。首先,我們將概述一種逐步構建CTSD調(diào)制器環(huán)路的方法,首先采用常見的閉環(huán)反相放大器配置,然后與ADC和DAC組合在一起。最后,我們將評估所構建電路的基本∑-?功能。
第1步:回顧閉環(huán)反相放大器配置
CTSD ADC的一個關鍵優(yōu)勢是它提供一個易于驅動的連續(xù)電阻輸入,而非傳統(tǒng)的前置開關電容采樣器。反相放大器電路具有類似的輸入阻抗概念,我們將其用作構建CTSD調(diào)制器環(huán)路的起始模塊。
閉環(huán)運算放大器配置一直是以高保真度復制模擬輸入的首選方法,圖1所示為其中一種常見的運算放大器配置,稱為反相放大器配置。1衡量保真度的一個指標是輸出與輸入增益的比值,采用∑-?術語表示,也稱為信號傳遞函數(shù)(STF)。確定影響STF的參數(shù)需要進行電路分析。
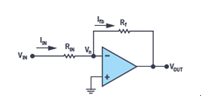
圖1.采用反相放大器配置的閉環(huán)運算放大器
為了鞏固我們的數(shù)學知識,我們來回顧一下著名VOUT ?VIN的由來。首先,我們假設運算放大器A的開環(huán)增益無窮大。根據(jù)這一假設,運算放大器的負輸入Vn將處于地電位。在這里應用基爾霍夫定律

將其映射到VOUT和VIN,我們得到增益或STF為

接下來,我們放棄不切實際的無限增益假設,在運算放大器的有限增益A下重新推導STF,則STF如下式所示
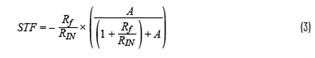
在這里,教科書通常會描述每個參數(shù)RIN、Rf和A的靈敏度。在本示例中,我們繼續(xù)構建CTSD環(huán)路。
第2步:將離散部件引入放大器
我們的ADC信號鏈需要數(shù)字版本的VIN。下一步,我們要在此電路中引入數(shù)字部件。我們沒有按傳統(tǒng)方式直接在輸入信號端放置一個采樣ADC,而是嘗試其他方法,在放大器輸出之后放置一個典型ADC器件來獲取數(shù)字信號數(shù)據(jù)。但是,ADC的輸出不能直接用作反饋,因為它必須是模擬電壓。因此,我們需要在ADC之后放置一個電壓數(shù)模轉換器(DAC),如圖2所示。
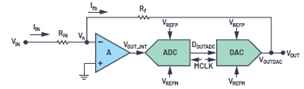
圖2.在反相放大器配置中引入ADC和DAC
采用ADC和DAC后,VOUT仍能表示VIN,但由于增加了數(shù)字部件,因此存在量化誤差。所以,從VIN到VOUT的信號流沒有變化。這里要注意的一點是,為了使環(huán)路功能相對于0 V保持對稱,并簡化數(shù)學推導,我們這樣選擇ADC和DAC的基準電壓,如下所示
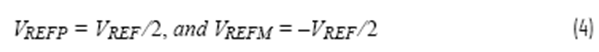
第3步:引入模擬累加器 — 積分器
圖2中的閉環(huán)配置是否穩(wěn)定?ADC和DAC均為在采樣時鐘MCLK下工作的離散元件。設計無延遲ADC或DAC一直是轉換器專家無法實現(xiàn)的夢想。由于這些環(huán)路元件采用時序控制,通常在一個時鐘沿進行輸入采樣,在另一個時鐘沿進行處理。因此,ADC和DAC組合輸出VOUT(即圖2中的反饋)需要延遲1個時鐘周期后才可用。
這種反饋延遲對穩(wěn)定性有影響嗎?我們來看看VIN是如何傳輸?shù)摹楹喕鹨姡覀兗僭OVIN = 1,RIN = 1,Rf = 1,運算放大器A的增益為100。在第一個時鐘周期,輸入電壓為1,DAC輸出反饋VOUT或VOUTDAC為0,并且在下一個時鐘沿前不可用。當我們跟蹤放大器和ADC的輸入和輸出反饋之間的誤差時,可以看到輸出一直呈指數(shù)增長,這在技術上稱為失控問題。
表1.時鐘沿采樣

這是因為ADC輸入對放大器獲得的瞬時誤差產(chǎn)生的影響;也就是說,甚至在獲得反饋之前,就能確定ADC會產(chǎn)生這種影響,而這是我們不希望的。如果ADC影響累積的平均誤差數(shù)據(jù),使得由于1個時鐘周期延遲反饋導致的誤差達到平均值,系統(tǒng)的輸出將受限。
積分器是平均累加器的等效模擬器件。環(huán)路增益仍然很高,但僅在低頻下很高,或者說在目標頻率帶寬下很高。這確保ADC不會出現(xiàn)任何可能導致失控情況的瞬時誤差。因此,現(xiàn)在將環(huán)路中的放大器改為積分器后接ADC和DAC,如圖3a所示。
第4步:簡化反饋電阻
這里的目標元件是DOUTADC,我們來重新布局環(huán)路元件,重點是將DOUTADC作為系統(tǒng)的輸出,如圖3b所示。接下來,我們來考慮DAC和Rf路徑的簡化。為此,我們先深入了解一下DAC。DAC的作用是將DIN數(shù)字信號轉換為與基準電壓成比例的等效模擬電流或電壓。為了進一步擴大基準電壓源連續(xù)性的優(yōu)勢,我們考慮采用一個基于梯形電阻的通用DAC架構,該電阻對于基準電壓源沒有開關負載。我們來看測溫電阻DAC,2根據(jù)等式5,它將DIN轉換為DAC電流。

其中VREF = VREFP – VREFM,即DAC的總基準電壓。
DIN = 測溫代碼中的數(shù)字輸入
Rf = 反饋電阻;拆分為每個單位元件
N = 位數(shù)
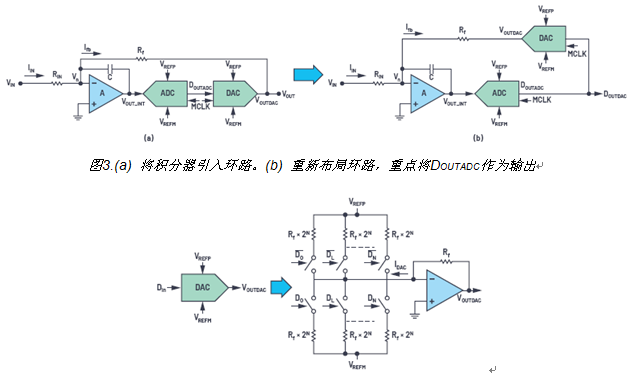
圖4.通用測溫電阻DAC
為了獲得電壓輸出,使用跨阻配置的運算放大器進行I至V轉換,3 如圖4所示。因此,

回到圖3b的離散環(huán)路,此VOUTDAC再次通過反相放大器的反饋電阻被轉換回電流Ifb,即信號流為IDAC → VOUTDA C → Ifb。通過數(shù)學式表示為:

從上面的信號流和公式可以看出,將VOUTDAC轉換為Ifb是一個冗余步驟,可以繞過。刪除冗余元件,并且為了簡單起見,將(VREFP – VREFM)表示為VREF,我們來重新繪制環(huán)路,如圖5所示。
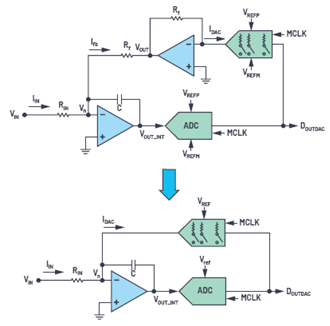
圖5.刪除冗余I至V轉換部分和反饋電阻。
瞧!我們構建了一個一階Σ-Δ環(huán)路!將所有已知元件即反相放大器、ADC和DAC接在一起。
第5步:了解過采樣
至此我們掌握了CTSD環(huán)路的構建,但尚未認識到這個特殊環(huán)路的獨特之處。首先來了解過采樣。ADC數(shù)據(jù)僅在有足夠的采樣和數(shù)字化數(shù)據(jù)點來提取或解讀模擬信號信息時才有用。奈奎斯特準則建議,為了忠實地重構輸入信號,ADC的采樣頻率至少應該是信號頻率的兩倍。如果我們在這個最低要求基礎上繼續(xù)增加更多的數(shù)據(jù)點,將會進一步減少解讀誤差。遵循這一思路,在∑-?中選擇的采樣頻率要比建議的奈奎斯特頻率高得多,這稱為過采樣。過采樣4將總噪聲分散到更高的頻率范圍,有助于減少目標頻帶中的量化噪聲,如圖6所示。
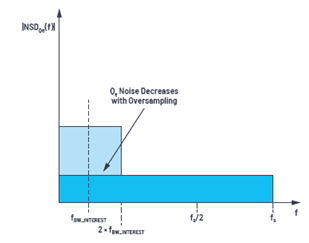
圖6.奈奎斯特采樣和過采樣之間的噪聲譜密度比較
第6步:了解噪聲整形
當∑-△專家使用噪聲傳遞函數(shù)(NTF)或噪聲整形等術語時,信號鏈設計人員不應該感到迷茫,4我們的下一步將幫助他們直觀地了解∑-△轉換器特有的這些術語。我們來回顧一下簡單的反相放大器配置以及放大器輸出端產(chǎn)生的誤差Qe,如圖7所示。
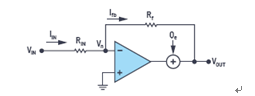
圖7.反相放大器配置中產(chǎn)生誤差
此誤差在輸出端的貢獻因素可量化為

從數(shù)學公式可以看出,誤差Qe由放大器的開環(huán)增益衰減,這再次表明了閉環(huán)的優(yōu)勢。
這種對閉環(huán)優(yōu)勢的理解可以延伸到CTSD環(huán)路中ADC的量化誤差Qe,此誤差是由于積分器輸出端連續(xù)信號的數(shù)字化引起的,如圖8所示。
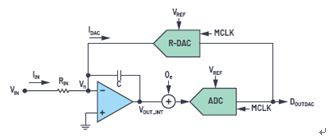
圖8.∑-△環(huán)路中產(chǎn)生量化誤差Qe
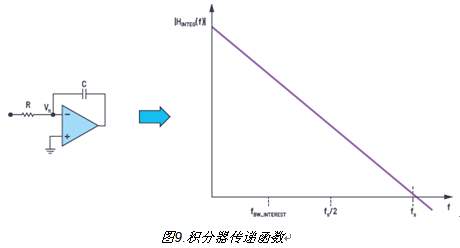
我們現(xiàn)在可以直觀地得出結論,此Qe可通過積分器衰減。積分器TF為|HINTEG (f)|= 1/|s × RC| = 1/2πfRC,其相應的頻域表示如圖9所示。其曲線等同于在低頻下具有高增益的低通濾波器曲線,增益隨頻率的增加呈線性減小。相應地,Qe的衰減變化與高通濾波器的表現(xiàn)類似。
此衰減因數(shù)的數(shù)學表示是噪聲傳遞函數(shù)。讓我們暫時忽略ADC中的采樣器和DAC中的開關。NTF即VOUTADC / Qe可通過與反相放大器配置一樣的方式來評估,其在頻域中的變化曲線與高通濾波器曲線類似,如圖10所示。
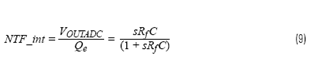
在目標頻帶中,量化噪聲被完全衰減并推至“與我們無關”的高頻。這就是所謂的噪聲整形。
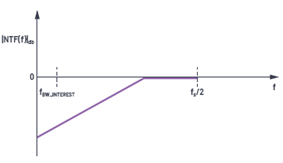
圖10.沒有采樣器時的噪聲傳遞函數(shù)——具有高通濾波器曲線
由于環(huán)路中有采樣器,量化噪聲整形類比保持不變。不同的是,NTF頻率響應將在每個fS倍數(shù)處復制圖像,如圖10所示,從而在采樣頻率的每個整數(shù)倍處產(chǎn)生陷波。
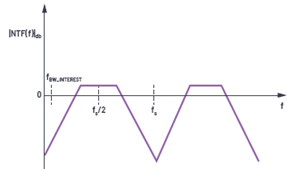
圖11.CTSD ADC的噪聲傳遞函數(shù)
∑-△架構的獨特之處在于,它將一個積分器和一個DAC環(huán)路放置在一個原始ADC(例如,4位ADC)周圍,通過過采樣和噪聲整形大幅減少目標頻率帶寬中的量化噪聲,使這個原始ADC變成一個16位或24位精密ADC。
這些一階CTSD ADC的基本原理現(xiàn)在可以擴展到任意階的調(diào)制器環(huán)路。采樣頻率、原始ADC規(guī)格和環(huán)路階數(shù)是受ADC性能要求驅動的主要設計決策因素。
第7步:利用數(shù)字濾波器完成CTSD調(diào)制器
一般來講,在ADC信號鏈中,數(shù)字化數(shù)據(jù)由外部數(shù)字控制器進行后處理,以提取任何信號信息。我們現(xiàn)在知道,在∑-?架構中,將對信號進行過采樣。如果將此過采樣數(shù)字數(shù)據(jù)直接提供給外部控制器,就需要處理大量冗余數(shù)據(jù)。這會導致數(shù)字控制器設計中的功率和電路板空間成本開銷過大。因此,在數(shù)據(jù)提供給數(shù)字控制器之前,在不影響性能的情況下,應有效地降低數(shù)據(jù)采樣。此過程稱為抽取,由數(shù)字抽取濾波器完成。圖11所示為具有片內(nèi)數(shù)字抽取濾波器的典型CTSD調(diào)制器。
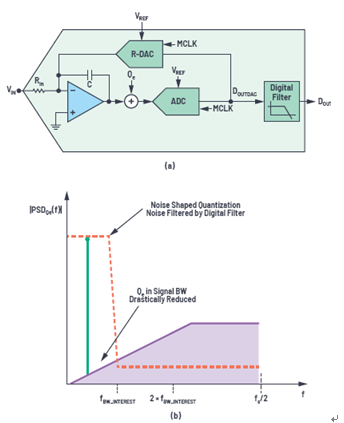
圖12.(a) 從模擬輸入到數(shù)字輸出的CTSD ADC調(diào)制器環(huán)路的方框圖。(b) 調(diào)制器輸出端和數(shù)字濾波器輸出端的輸入信號的頻譜表示。
圖12b所示為帶內(nèi)模擬輸入信號的頻率響應。在調(diào)制器的輸出端,我們看到對量化噪聲進行噪聲整形后,目標頻帶中的量化噪聲大幅降低。數(shù)字濾波器有助于衰減超出此目標頻率帶寬的整形后噪聲,這樣最終的數(shù)字輸出DOUT將處于奈奎斯特采樣速率。
第8步:了解CTSD ADC的時鐘靈敏度
現(xiàn)在,我們知道CTSD ADC如何保持輸入信號的連續(xù)完整性,這大大簡化了信號鏈的設計。此架構也有一些限制,主要是處理采樣時鐘MCLK。CTSD調(diào)制器環(huán)路的工作原理是累積IIN和IDAC之間的誤差電流。此積分值中的任何誤差都會導致環(huán)路中的ADC對此誤差進行采樣,并在輸出中反映出來。對于我們的一階積分器環(huán)路,在恒定IIN和IDAC的Ts采樣時間段的積分值表示為
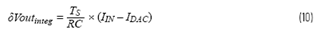
對于0輸入,會影響此積分誤差的參數(shù)包括
MCLK頻率:如等式10所示,如果MCLK頻率縮放,控制積分斜率的RC系數(shù)也需要重新調(diào)整以得到相同的積分值。這意味著CTSD調(diào)制器針對固定的MCLK時鐘頻率進行調(diào)諧,無法支持變化的MCLK。
MCLK抖動:DAC代碼以及IDAC會改變每個時鐘時間段Ts。如果IDAC時間段隨機改變,平均積分值就會不斷變化,如圖13所示。因此,采樣時鐘時間段中以抖動形式出現(xiàn)的任何誤差都會影響調(diào)制器環(huán)路的性能。
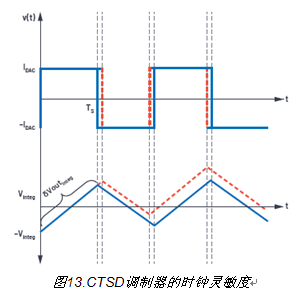
出于上述原因,CTSD ADC對MCLK的頻率和抖動敏感。5但是,ADI已經(jīng)找到了解決這些誤差問題的方法。例如,生成精確的低抖動MCLK并在系統(tǒng)中傳送到ADC的挑戰(zhàn),可以通過在ADC附近使用一個低成本的本地晶體振蕩器來解決。固定采樣頻率周圍的誤差問題已通過使用創(chuàng)新的異步采樣速率轉換(ASRC)解決,該轉換無需考慮固定采樣MCLK,可以為數(shù)字控制器提供獨立可變的數(shù)字輸出數(shù)據(jù)速率。本系列后續(xù)文章將詳細介紹更多相關信息。
第9步:瞧!一切準備就緒,可以向伙伴們解釋CTSD概念了!
第1部分強調(diào)了CTSD ADC的某些信號鏈優(yōu)勢,而第2部分重點介紹從第1步到第6步使用閉環(huán)運算放大器配置概念構建調(diào)制器環(huán)路的見解。圖11a也有助于我們看清這些優(yōu)勢。
CTSD ADC的輸入阻抗等同于反相放大器的輸入阻抗,它是電阻性的,且易于驅動。通過使用創(chuàng)新技術,使得調(diào)制器環(huán)路的DAC所使用的基準電壓源也成為電阻性。ADC的采樣器位于積分器之后,并非直接放在輸入端,從而可實現(xiàn)對目標頻帶之外干擾源的固有混疊抑制。在本系列接下來的幾篇文章中,我們將深入探討這些優(yōu)勢及其對信號鏈的影響。在下一篇文章中,我們將首先介紹最獨特的優(yōu)勢:固有混疊抑制。敬請關注第3部分,了解固有混疊抑制及其使用一組新的測量和性能參數(shù)實現(xiàn)量化的詳細信息,這些參數(shù)首次通過基于CTSD架構的AD4134引入。


