摘 要: 對(duì)一種新的部分傳輸序列" title="部分傳輸序列">部分傳輸序列方法(PTS)進(jìn)行了分析和仿真,并通過(guò)預(yù)設(shè)門(mén)限找到加權(quán)因子的方法來(lái)降低計(jì)算的復(fù)雜度。該方法與最優(yōu)PTS方法相比,性能有少許下降,但復(fù)雜度顯著降低。
關(guān)鍵詞: OFDM系統(tǒng) 峰均功率比" title="峰均功率比">峰均功率比 部分傳輸序列
正交頻分復(fù)用(OFDM)技術(shù)是一種高速數(shù)據(jù)傳輸技術(shù),因能有效消除符號(hào)間干擾(ISI),減小接收機(jī)內(nèi)均衡的復(fù)雜度,得到了廣泛的應(yīng)用。但是,其致命的缺陷就是峰均功率比(PAPR)較高。為減小PAPR,已經(jīng)提出了很多方法,包括信號(hào)失真技術(shù)、編碼技術(shù)" title="編碼技術(shù)">編碼技術(shù)和擾碼技術(shù)。
PTS方法是一種較好的減小PAPR的方法,不引入畸變,且適用于任何星座。它是由Muller和Huber[1]提出的。但是PTS方法的復(fù)雜度較高,因此,本文提出了一種減小PTS計(jì)算復(fù)雜度的方法。
1 減小PAPR的方法
1.1 PTS方法
圖1給出了PTS方法的框圖。其中輸入的數(shù)據(jù)符號(hào)被分成若干子塊" title="子塊">子塊,再組合這些子塊,以減小PAPR。
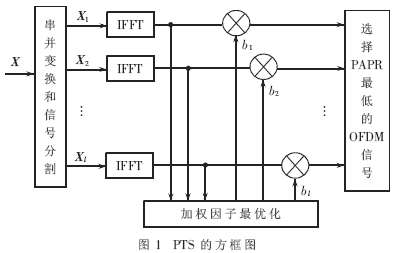
首先利用向量來(lái)定義數(shù)據(jù)符號(hào)X=[X1X2…XN]T。然后把向量X分割為M個(gè)子塊,分別由Xl{l=1,…,M}表示,假設(shè)每個(gè)子塊中所包括的子載波數(shù)量是相同的,將M這個(gè)子塊按如下方式組合起來(lái):
通過(guò)適當(dāng)?shù)剡x擇加權(quán)因子,使式(2)的峰值信號(hào)得到最優(yōu)化。
1.2 Cimini算法
在文獻(xiàn)[2]中,Cimini和Sollenberger提出一種次最優(yōu)的組合算法,僅使用二進(jìn)制加權(quán)因子。這種算法概括如下:
(1)假設(shè)bl=1,l=1,…,M計(jì)算PAPR;
(2)l=2;
(3)令bl=-1,重新計(jì)算PAPR0′。
(4)如果PAPR0>PAPR0′,則bl=-1,否則bl=1;
(5)l=l+1;
(6)重復(fù)(3)~(5)步,直到所有的M種可能試完為止。
在Cimini方法中,只需要計(jì)算M步就可以得到所需要的加權(quán)因子了。
2 提出的PRPA減小的方法
2.1 提出的尋找次最優(yōu)加權(quán)因子的方法
文獻(xiàn)[3]提出了一種更簡(jiǎn)單的次最優(yōu)的方法,這種方法概括如下:
(1)假設(shè)bl=1,l=1,…,M,計(jì)算PAPR0;
(2)如果PAPR0小于設(shè)定的門(mén)限L,則停止優(yōu)化;
(3)否則l=1;
(4)令bl=-1,重新計(jì)算PAPR1l;
(5)如果PAPR1l>L,則BL=-1,否則BL=1;
(6)l=l+1;
(7)重復(fù)(4)~(6)步,直到所有的M種可能試完為止。
2.2 對(duì)子塊的門(mén)限檢測(cè)
OFDM信號(hào)的功率分布是均值為0、自由度為2的x2分布,從OFDM信號(hào)功率特性可以推斷出很多OFDM存在低的PAPR,PTS方法中尋找加權(quán)因子的計(jì)算復(fù)雜度可以采用一個(gè)門(mén)限來(lái)減小[4],一旦PAPR下降到門(mén)限以下,則停止尋找。本文中采用了門(mén)限來(lái)減小計(jì)算的復(fù)雜度,門(mén)限可以由CCDF計(jì)算出來(lái)。假設(shè)子載波數(shù)為N,子塊為M個(gè),PAPR0超過(guò)某一的概率可以表示為:
當(dāng)門(mén)限設(shè)置高于L,CCDF下降,在保證性能不下降的情況下,門(mén)限應(yīng)該設(shè)置的低一些。從(4)式可以看出對(duì)一個(gè)塊取得0.1%CCDF的最小門(mén)限為11.19dB,4塊是8.96dB,8塊是8.35dB。
3 實(shí)驗(yàn)結(jié)果和結(jié)論
為了評(píng)價(jià)和比較提出次最優(yōu)PTS的性能,采用了計(jì)算機(jī)仿真,仿真參數(shù)如表1所示。

在對(duì)比中,定義兩種參數(shù):CCDF和計(jì)算復(fù)雜度CC。

其中:Ii為每個(gè)OFDM符號(hào)的迭代次數(shù)" title="迭代次數(shù)">迭代次數(shù),N是OFDM符號(hào)數(shù)。
M=4的pr(PAPR>PAPR0)CCDF如圖2(a)所示,原始OFDM幀0.1%PAPR是11.5dB,PTS改進(jìn)了2.6dB,而Cimini方法改進(jìn)了2.2dB。4個(gè)子塊,門(mén)限取8.35dB和8.96dB,其PAPR與傳統(tǒng)的PTS方法相同。M=8的CCDF如圖2(b)所示,用PTS的OFDM幀0.1%PAPR是7.9dB,而Cimini方法僅損失1dB,門(mén)限為8.08dB和8.35dB時(shí),損失僅為0.6dB。以上方法的迭代次數(shù)如表2所示。從表2可以看出,用本文提到的方法,復(fù)雜度大大降低。
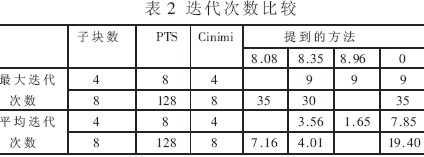
本文給出了一種次最優(yōu)的PTS方法,使用預(yù)設(shè)門(mén)限的方法來(lái)減小計(jì)算的復(fù)雜度。它與傳統(tǒng)的方法相比,性能下降很少,而復(fù)雜度可以降低很多。對(duì)于4個(gè)子塊提出的方法的性能與傳統(tǒng)的PTS一樣,而復(fù)雜度僅為傳統(tǒng)的PTS的20.6%;對(duì)于8個(gè)子塊,提出的方法性能比傳統(tǒng)的PTS稍微下降,而復(fù)雜度僅為傳統(tǒng)的PTS的3.1%。
參考文獻(xiàn)
1 S. H. Han, J. H. Lee. Reduction of PAPR of an OFDM signal by partial transmit sequence technique with educed complexity. IEEE Globecom, 2003:1326~1329
2 L. J. Cimini, Jr. and N. R. Sollenberger. Peak-to-average power ratio reduction of an OFDM signal using partial transmit sequence. IEEE Commun. Lett,2000;4(3):86~88
3 Oh-Ju Kwon and Yeong-Ho Ha. Multi-carrier PAP reduction method using sub-optimal PTS with threshold. IEEE Transactions on broadcasting,2003;49(2):232~236
4 A. D. S. Jayalath and C. Tellambura. Adaptive PTS approach for reduction of peak-to-average power ratio of OFDM signal. Electronics Letters, 2000;36(14):1226~1228


