摘 要: 在原相移器設(shè)計(jì)算法的基礎(chǔ)上,通過增加一個(gè)偽隨機(jī)數(shù)生成函數(shù)來選擇異或節(jié)點(diǎn)的相移器設(shè)計(jì)算法。實(shí)驗(yàn)結(jié)果表明,此算法不僅克服了原算法設(shè)計(jì)的相移器造成LFSR扇出" title="扇出">扇出過大的缺點(diǎn),而且提高了偽隨機(jī)測試" title="偽隨機(jī)測試">偽隨機(jī)測試故障的覆蓋率。
關(guān)鍵詞: 偽隨機(jī)測試 混合模式測試 相移器 線性反饋移位寄存器 故障覆蓋率
集成電路的發(fā)展已進(jìn)入SoC時(shí)代,可將各種不同類型的IP芯核集成在一塊芯片上,構(gòu)成一個(gè)完整的系統(tǒng),既能加快開發(fā)進(jìn)度,又能提高系統(tǒng)整體性能。但集成電路的測試卻面臨越來越多的挑戰(zhàn),如不同類型的IP核測試方法不同,使得集成電路測試的復(fù)雜性大大提高。此外受芯片引腳數(shù)目的限制,IP芯核的I/O端口缺乏可觀性和可測性。芯片的頻率普遍高于自動測試設(shè)備(ATE)的頻率,芯片的全速測試變得困難。內(nèi)建自測試(BIST)是解決集成電路測試的有效方法之一。BIST將測試模式生成器、測試過程控制和測試響應(yīng)評價(jià)功能模塊嵌入在被測電路(CUT)上,擺脫了對ATE的依賴。這不僅是解決SoC測試問題的有效方法之一,也是SoC測試發(fā)展的方向[1]。
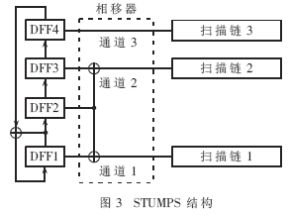
從測試模式生成器的角度,可將BIST分為偽隨機(jī)測試[2]、確定測試[3]和混合模式測試[4]。偽隨機(jī)測試是硬件開銷最少的BIST測試方法,目前最流行的偽隨機(jī)測試序列生成器是線性反饋移位寄存器(LFSR)。LFSR是由一系列D觸發(fā)器經(jīng)反饋線連接而成。LFSR有兩類,兩類LFSR互為對偶,如圖1所示。圖1所示LFSR都可用特征多項(xiàng)式1+h1x1+…+hn-1xn-1+xn表示。若hi=1表示第xi個(gè)觸發(fā)器的輸出經(jīng)反饋線連接到異或門。
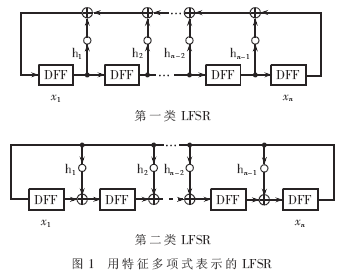
圖1所示LFSR也可用矩陣M和D來表示。M為第一類LFSR的伴隨矩陣,D為第二類LFSR的伴隨矩陣。容易證明,MT=D-1[5]。

通過伴隨矩陣,可以得到經(jīng)過某個(gè)時(shí)鐘周期后LFSR的狀態(tài)。考慮第一類LFSR,設(shè)其值為V0=(x1,x2,…,xn),則經(jīng)過P個(gè)時(shí)鐘周期后,其值VP=V0×MP,即由LFSR狀態(tài)V0向前模擬P個(gè)時(shí)鐘周期可得到VP。由上式可得V0=VP×M-P,也可稱為由LFSR狀態(tài)VP向后模擬P個(gè)時(shí)鐘周期得到V0。
在集成電路可測試性設(shè)計(jì)中,為節(jié)省測試時(shí)間,一般采用多掃描鏈的設(shè)計(jì)。若僅采用LFSR做為偽隨機(jī)序列" title="偽隨機(jī)序列">偽隨機(jī)序列生成器,不同掃描鏈間的數(shù)據(jù)存在很大的相關(guān)性,如圖2所示。
相鄰的兩個(gè)掃描鏈間的數(shù)據(jù)只差一個(gè)相位,大大降低了偽隨機(jī)測試的故障覆蓋率" title="故障覆蓋率">故障覆蓋率。為降低數(shù)據(jù)間的相關(guān)性,通常在LFSR和多掃描鏈間加上由異或門組成的移相器,這種結(jié)構(gòu)稱為STUMPS結(jié)構(gòu),如圖3所示。

?
相移器打破了掃描鏈間數(shù)據(jù)的高度相關(guān)性,使相鄰掃描鏈中的數(shù)據(jù)相差多個(gè)相位,提高了偽隨機(jī)測試的故障覆蓋率。因此,相移器的設(shè)計(jì)對偽隨機(jī)測試的成功有著至關(guān)重要的作用。
文獻(xiàn)[5]、文獻(xiàn)[6]提出了相移器的設(shè)計(jì)算法,但此算法設(shè)計(jì)的相移器要求LFSR的某幾位有很高的扇出,在實(shí)際的設(shè)計(jì)中,要增加反相器來增強(qiáng)這些節(jié)點(diǎn)的驅(qū)動能力,造成芯片的面積和時(shí)延增大。本文在分析和研究此算法的基礎(chǔ)上,對其缺點(diǎn)進(jìn)行了改進(jìn)。通過增加一個(gè)偽隨機(jī)數(shù)生成函數(shù)選擇相移器的通道,使得LFSR節(jié)點(diǎn)扇出分布相對均勻。實(shí)驗(yàn)結(jié)果表明本算法是一種高效、實(shí)用的相移器設(shè)計(jì)算法。
1 相移器理論推導(dǎo)及算法
由圖3可知相移器的通道輸出都是LFSR某幾位的異或,為描述通道的輸出值,引入了相移器選擇矢量。如圖3通道2的選擇矢量為S=(0110),表示LFSR第2個(gè)節(jié)點(diǎn)和第3個(gè)節(jié)點(diǎn)的異或值作為通道2的輸出。設(shè)某一時(shí)刻LFSR的值為V=(v1,v2,v3,v4),則經(jīng)過P個(gè)時(shí)鐘脈沖" title="時(shí)鐘脈沖">時(shí)鐘脈沖后,通道2的輸出值可表示為OUT2=V×MP×ST。ST表示S的轉(zhuǎn)置。芯片實(shí)現(xiàn)時(shí)通常要求相移器有較小時(shí)延和面積,因此相移器的每個(gè)通道最多為 3 個(gè)節(jié)點(diǎn)的異或,即每一個(gè)通道選擇矢量最多有 3 位為“1”。且為了打破不同掃描鏈間數(shù)據(jù)的相關(guān)性,任意兩個(gè)通道之間的相位要大于等于某個(gè)確定的值。構(gòu)建n個(gè)通道的相移器的問題等價(jià)于從LFSR的值域中選擇n個(gè)值作為選擇矢量,每一個(gè)選擇矢量中的“1”的個(gè)數(shù)不大于3,且任意兩個(gè)通道之間的相位要大于等于確定的值P。
設(shè)計(jì)相移器的關(guān)鍵問題是選擇通道,使不同的通道輸出之間的相位大于等于某一個(gè)確定的值P,這主要利用LFSR的性質(zhì)。本文對此性質(zhì)給出證明。
定理1:設(shè)有通道選擇矢量Si和Sj,若將Si做為第二類(第一類)LFSR的初始值,經(jīng)過P 個(gè)時(shí)鐘脈沖后LFSR值變?yōu)镾j,則以其對偶的LFSR為偽隨機(jī)序列發(fā)生器,以Si和Sj作為通道選擇矢量構(gòu)造的相移器的兩個(gè)通道i和j輸出序列相差P個(gè)相位。
下面以第一類LFSR作為偽隨機(jī)序列發(fā)生器來證明此定理。
證明: 設(shè)第一類LFSR 的伴隨矩陣為M,第二類LFSR的伴隨矩陣為D。
比較式(1)和式(4),可知通道i和j的輸出序列相差P個(gè)相位。
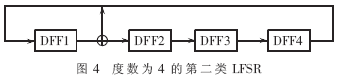
下面舉例來說明定理1。如圖4所示的第二類LFSR,若其初始值Si為(0110),經(jīng)過15個(gè)脈沖后,其狀態(tài)變?yōu)?1100),記為Sj。則可驗(yàn)證圖3所示的通道2和通道3相差15個(gè)相位,其中Si和Sj為通道2和通道3的選擇矢量。
文獻(xiàn)[5]、文獻(xiàn)[6]提出了兩種相移器的綜合算法,這里介紹執(zhí)行速度快的算法(以第一類LFSR作為偽隨機(jī)序列生成器構(gòu)建相移器),記為算法A:
(1)生成“1”的個(gè)數(shù)不大于3的LFSR值的被選列表,令變量i=1,且將選擇矢量列表清空;
(2)從被選列表中取第i個(gè)值,利用該值為第二類LFSR的初始值,然后前向仿真 P個(gè)時(shí)鐘脈沖,后向仿真P個(gè)時(shí)鐘脈沖;
(3)如仿真中出現(xiàn)的值與選擇矢量列表中的值重復(fù),則拋棄這次選擇的值,否則將其加入選擇矢量列表;
(4)如果選擇矢量個(gè)數(shù)達(dá)到要求即停止,否則i加1,從第2步開始運(yùn)行。
通過第2步與第3步就能保證選擇出來的通道至少相差P個(gè)相位。通過一個(gè)4階LFSR的實(shí)例來說明其綜合過程。第1步生成的被選列表為:
{(1),(2),(3),(4),(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),(1,2,3),(1,2,4),(1,3,4),(2,3,4)}
如列表中(1,2,3)代表的是選擇矢量(1110)。被選列表中第1個(gè)值(1)是符合條件的,將其添加到選擇矢量列表中,然后再按照順序判斷(2)、(3)、(4)、(1,2)、(1,3)等組合是否滿足條件。
從上述過程可看出此算法存在的缺點(diǎn):產(chǎn)生的相移器對LFSR的某幾位輸出要求很高的扇出。這是因?yàn)槊看卧撍惴ǘ际前凑毡贿x列表中值的順序來選擇符合條件的矢量,一旦選擇矢量個(gè)數(shù)達(dá)到要求,算法就停止,后面符合條件的選擇矢量沒有得到利用。集成電路設(shè)計(jì)中,扇出過大,將會造成芯片面積增大,信號的建立時(shí)間過長等問題,最終可能導(dǎo)致設(shè)計(jì)的失敗。本文采用的算法沒有按照被選列表中值的順序來選擇符合條件的選擇矢量,而是通過一個(gè)偽隨機(jī)數(shù)生成函數(shù)來選擇被選列表中的值,記為算法B,其算法如下:
(1)生成“1”的個(gè)數(shù)不大于3的LFSR值的被選列表,記列表中值的個(gè)數(shù)為k。令變量i=1,且將選擇矢量列表清空;
(2)從被選列表中取第i個(gè)值,利用該值為第二類LFSR的初始值,然后前向仿真P個(gè)時(shí)鐘脈沖,后向仿真P個(gè)時(shí)鐘脈沖;
(3)如仿真中出現(xiàn)的值與選擇矢量列表中的值重復(fù),則拋棄這次選擇的值,否則將其加入選擇矢量列表;
(4)如果選擇矢量個(gè)數(shù)達(dá)到要求即停止,否則i=rand()%k+1,從第2步開始運(yùn)行。
其中rand()為產(chǎn)生偽隨機(jī)的非負(fù)整數(shù)的函數(shù)。其函數(shù)實(shí)現(xiàn)如下:
int rand()
{next=next*1103515245+12345;
return((unsigned int)(next/65536)%32768);
}
next為無符號長整型靜態(tài)變量,初始值為1。rand()函數(shù)輸出一系列在0~32 767之間均勻分布的偽隨機(jī)數(shù)值,產(chǎn)生的序列是可重現(xiàn)的,即程序每次運(yùn)行都產(chǎn)生同樣的一系列隨機(jī)數(shù)。“%”為取余運(yùn)算。在實(shí)際的設(shè)計(jì)中,為減小芯片面積,LFSR度數(shù)為48時(shí),就可滿足百萬門規(guī)模的設(shè)計(jì)需要。此時(shí)被選列表中元素的個(gè)數(shù)為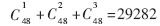 ,因此rand()函數(shù)返回值可取得被選列表中的所有值。從后面實(shí)驗(yàn)結(jié)果可看出,本算法構(gòu)建的相移器不僅克服了LFSR某幾位扇出過大的問題,而且通過此相移器生成的偽隨機(jī)序列在電路的故障覆蓋率方面也有所提高。
,因此rand()函數(shù)返回值可取得被選列表中的所有值。從后面實(shí)驗(yàn)結(jié)果可看出,本算法構(gòu)建的相移器不僅克服了LFSR某幾位扇出過大的問題,而且通過此相移器生成的偽隨機(jī)序列在電路的故障覆蓋率方面也有所提高。
2 實(shí)驗(yàn)結(jié)果及分析
表1為兩種算法構(gòu)建相移器時(shí),對LFSR扇出的比較。選取第一類LFSR為基礎(chǔ)構(gòu)建相移器,度數(shù)為24,特征多項(xiàng)式為x24+x4+x3+x+1,相移器的通道數(shù)為100,兩通道間的相位差p為1024。
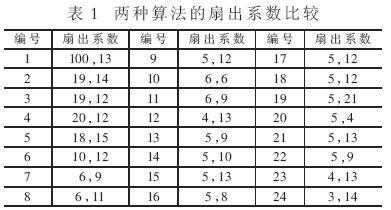
第1、3、5列為LFSR觸發(fā)器的編號,其余列為兩種算法扇出系數(shù)的比較。逗號前為算法A生成的相移器所需LFSR各位觸發(fā)器的扇出系數(shù),逗號后為本算法的扇出系數(shù)。從表1可看出,本算法LFSR各觸發(fā)器扇出要求相比算法A要均勻。如算法A對第1個(gè)觸發(fā)器的輸出是100,而本算法為13。
混合模式的BIST首先對電路進(jìn)行偽隨機(jī)測試,然后對偽隨機(jī)測試未測試到的故障采用自動測試模式生成算法(ATPG),對確定的測試向量進(jìn)行測試。這里對國際上標(biāo)準(zhǔn)的ISCAS-89[8]部分電路做了實(shí)驗(yàn),這些電路在10 000個(gè)偽隨機(jī)模式之后仍有不可測試的故障。表2是LFSR通過兩種算法設(shè)計(jì)的相移器生成10 000個(gè)偽隨機(jī)模式對電路故障覆蓋率的比較。選取LFSR度數(shù)為24,電路掃描鏈數(shù)量為48,LFSR初始值為(1010…10)。第1列為電路名,第2列為算法A設(shè)計(jì)的相移器生成的偽隨機(jī)序列達(dá)到的故障覆蓋率,第3列為本算法的故障覆蓋率。
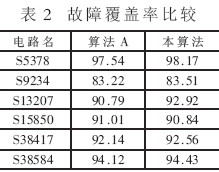
從表2可看出,除S15850外,本算法設(shè)計(jì)的相移器生成的偽隨機(jī)序列故障覆蓋率都高于算法A生成的相移器。這是因?yàn)長FSR的扇出分布比較均勻,各條掃描鏈間的相關(guān)性進(jìn)一步減小,從而提高偽隨機(jī)序列的測試故障覆蓋率。而在算法A中,LFSR第1號觸發(fā)器的扇出系數(shù)較大,受此觸發(fā)器影響的掃描鏈較多,這些掃描鏈間的關(guān)系也相對要大一些。
本文提出了通過一個(gè)偽隨機(jī)數(shù)生成函數(shù)來選擇異或節(jié)點(diǎn)的相移器設(shè)計(jì)算法。實(shí)驗(yàn)結(jié)果表明,與原算法相比,本算法不僅克服了原算法扇出過大的缺點(diǎn),而且生成的偽隨機(jī)序列對集成電路測試的故障覆蓋率也有所提高,在偽隨機(jī)測試和混合模式測試中有一定的實(shí)用價(jià)值。
參考文獻(xiàn)
[1] BUSHNELL M L,AGRAWAL D V.Essentials of electronic testing for digital,memory and mixed-signal VLSI circuits.USA:Kluwer Academic Publishers,2000.
[2] WUNDERLICH H J,HELLEBRAND S.The pseudo-exhaus-tive test of sequential circuits.Proc Of? International Test Conference,1989:19-27.
[3] 梁華國,聚貝勒.海倫布昂特,漢斯-耶西姆.馮特利西.一種基于折疊計(jì)數(shù)器重新播種的確定自測試方案.計(jì)算機(jī)研究與發(fā)展,2001,38(8).
[4] 梁華國,將翠云.使用雙重種子壓縮的混合模式自測試.計(jì)算機(jī)研究與發(fā)展,2004,41(1).
[5] JANUSZ R,NAGESH T,JERZY T.Automated synthesis of large phase shifters for built-in seft-test.Proc of International Test Conference,1998:1047-1056.
[6] JANUSZ R,JERZY T.Design of phase shifters for BIST? applications.Proc VLSI Test Symp,1998,218-224.