OFDM" target="_blank">OFDM(正交頻分復(fù)用)是一種高效的多載波調(diào)制技術(shù),其最大的特點是傳輸速率高,具有很強的抗碼間干擾和信道選擇性衰落能力。OFDM最初用于高速MODEM、數(shù)字移動通信和無線調(diào)頻信道上的寬帶數(shù)據(jù)傳輸,隨著IEEE802.11a協(xié)議、BRAN(Broadband Radio Access Network)和多媒體的發(fā)展,數(shù)字音頻廣播(DAB)、地面數(shù)字視頻廣播((DVB-T)和高清晰度電視((HDTV)都應(yīng)用了OFDM技術(shù)。
OFDM利用離散傅立葉反變換/離散傅立葉變換(IDFT/DFT)代替多載波調(diào)制和解調(diào),調(diào)制解調(diào)的核心是快速傅立葉運算單元,在進行蝴蝶運算時,不可避免的要進行大量的乘法運算。由于FPGA具有強大的并行處理和計算能力,以及豐富的存儲資源和邏輯運算資源,因此在FPGA器件上實現(xiàn)OFDM調(diào)制解調(diào)結(jié)構(gòu),具有很好的通用性和靈活性。
OFDM與系統(tǒng)框圖
OFDM的多個載波相互正交,一個信號內(nèi)包含整數(shù)個載波周期,每個載波的頻點和相鄰載波零點重疊,這種載波間的部分重疊提高了頻帶利用率。OFDM每個子信道的頻譜均為sinx/x形,各子信道頻譜相互交疊,但在每個子信道載頻的位置來自其他子信道的干擾為零,如圖1所示。

OFDM系統(tǒng)如圖2所示,OFDM系統(tǒng)的調(diào)制和解調(diào)分別由IFFT和FFT完成。首先將串行輸入數(shù)據(jù)d0,d1...,d(N-1)變換成并行數(shù)據(jù),接下來進行編碼和星座圖映射,得到頻域數(shù)據(jù)。經(jīng)過IFFT后相當于調(diào)制到正交的N個f0,f1,...,fN-1子載波,完成正交頻分復(fù)用。接下來加入循環(huán)前綴,進行并/串轉(zhuǎn)換,數(shù)/模轉(zhuǎn)換,再調(diào)制到高頻載波上發(fā)送。如果是基帶傳輸,則不需要進行載波調(diào)制。
在接收端進行相反的操作,使用N個相同的子載波進行N路解調(diào),再將這N路解調(diào)信號并串輸出,復(fù)現(xiàn)發(fā)送的原始信號。經(jīng)過FFT變換后的數(shù)據(jù)相當于將時域數(shù)據(jù)再轉(zhuǎn)換成頻域數(shù)據(jù),即完成了OFDM信號的解調(diào)。
OFDM調(diào)制原理雖然是用N個正交的載波分別調(diào)制N路子信道碼元序列,但實際中很難獨立產(chǎn)生N個正交的載波。所以O(shè)FDM多采用VLSI技術(shù),用FFT代替多載波調(diào)制和解調(diào)。當子信道數(shù)目比較多的時候,采用FFT可以大大減少系統(tǒng)的復(fù)雜度。而FPGA的并行乘法器和加法器結(jié)構(gòu)容易硬件實現(xiàn)OFDM的核心運算,有效地提高了OFDM調(diào)制解調(diào)速度。
軟件仿真與設(shè)計
隨著FPGA和VLSI的發(fā)展,大量的EAB(嵌入式陣列塊)、LE(邏輯單元)、內(nèi)嵌乘法器和高速FIFO存儲器帶來了OFDM/COFDM的實用化,為OFDM提供了硬件支持。軟件上可以采用MATLAB、硬件描述語言VHDL、QuartusⅡ等軟件進行仿真與設(shè)計。
仿真過程中采用了隨機信號作為輸入信號,經(jīng)過4QAM編碼映射后進行再IFFT調(diào)制,然后進入信道進行數(shù)據(jù)傳輸,每幀信號為512點;同時采用簡單的11點數(shù)字離散信道,其值為:[0.05 -0.063 0.088 -0.126 -0.25 0.9047 0.25 0 0.126 0.038 0.088]。
在一般OFDM系統(tǒng)中為使IFFT和FFT前后的信號功率保持不變,當N=2m(m為正整數(shù))時,作如下定義:
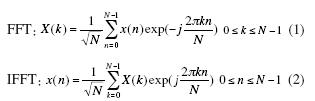
采用16位定點算法,這便意味著要考慮溢出問題。對于基-2 FFT,為了防止溢出,可以采用以下辦法:將每一個蝶算后的數(shù)據(jù)右移1bit,即相當于將該數(shù)做除2處理。這樣,加入總衰減比例因子,將比例因子分散到各步計算中。這種情況下,輸出不是原來定義的離散傅里葉變換,而是它的。而對于基-2 IFFT,這個比例因子正是公式中需要的,所以FPGA實現(xiàn)的IFFT便是最終結(jié)果。
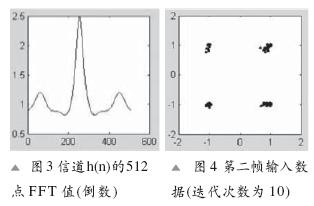
圖3和圖4分別是信道h(n)的FFT值(倒數(shù))和第二幀輸入數(shù)據(jù)(迭代次數(shù)10)。
調(diào)制過程中Matlab的IFFT結(jié)果同F(xiàn)PGA結(jié)果比較如表1所示。
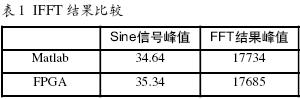
表1 IFFT結(jié)果比較
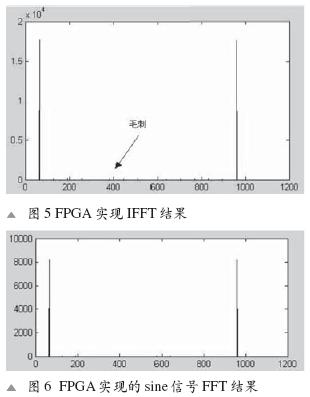
經(jīng)過FPGA的IFFT在非主頻率點上有一些小的誤差。這是因為在計算IFFT的時候,同樣因為舍入問題,在本該為零的點產(chǎn)生一些極小的數(shù)值,從而在信號顯示時出現(xiàn)這些毛刺。
對于表1,F(xiàn)FT峰值結(jié)果的誤差,是因為FPGA采用的是16bit定點算法,在程序中有很多舍位處理帶來的誤差。至于Sine信號峰值的不同,那是因為將FPGA實現(xiàn)的IFFT結(jié)果再進行Matlab的fft()計算,而IFFT的那些毛刺,必然在時域上產(chǎn)生影響。
在FPGA實現(xiàn)時,一般是在完成IFFT以后將結(jié)果暫時存放在RAM中,然后在從RAM里讀出數(shù)據(jù)時,采取部分重復(fù)讀取的方式,將一部分數(shù)據(jù)重復(fù)復(fù)制,從而形成循環(huán)前綴。這樣可以對連續(xù)的數(shù)據(jù)流進行變換處理,滿足系統(tǒng)的實時性要求。

解調(diào)過程中Matlab的FFT結(jié)果同F(xiàn)PGA結(jié)果比較如表2所示。
表2 FFT結(jié)果比較
從表2可以看出,F(xiàn)PGA的結(jié)果同Matlab的結(jié)果基本相同,只是FFT峰值有些不同。這也因為FPGA采用的是16bit定點算法,在程序中有很多舍位處理。但 FPGA的結(jié)果是將原小數(shù)信號變成整數(shù)后再進行處理的,當最后再轉(zhuǎn)換成小數(shù)后,結(jié)果將是一致的。
結(jié)語
OFDM信道調(diào)制解調(diào)的關(guān)鍵是一對離散傅里葉變換。程序可以由Verilog HDL模塊進行設(shè)計,用相應(yīng)的模塊仿真程序TESTBENCH進行功能仿真,經(jīng)過波形仿真和結(jié)果驗證后,將程序下載到FPGA中實現(xiàn)。同時,Verilog HDL仿真結(jié)果與MATLAB中函數(shù)fft()以及ifft()的輸出結(jié)果進行比較(采用的是浮點運算),得出圖形和數(shù)據(jù)的比較結(jié)果。
結(jié)果表明,用FPGA實現(xiàn)OFDM信道調(diào)制解調(diào)與MATLAB仿真結(jié)果基本一致,具有良好的性能和較高的效率。

