微電子學(xué)的發(fā)展徹底改變了計(jì)算機(jī)的設(shè)計(jì)：集成電路技術(shù)增加了能夠安裝到單個(gè)芯片中的元器件數(shù)目及其復(fù)雜度,。因此，采用這種技術(shù)可以構(gòu)建低成本,、專(zhuān)用的外圍器件,，從而迅速地解決復(fù)雜的問(wèn)題。
        大規(guī)模集成電路（VLSI）技術(shù)明確地指出：簡(jiǎn)單和規(guī)則的互連導(dǎo)致廉價(jià)的實(shí)現(xiàn)方式以及高密度,，而高密度能夠?qū)崿F(xiàn)高性能和低開(kāi)銷(xiāo),。有鑒于此，我們致力于設(shè)計(jì)并行的運(yùn)算法則,，其擁有簡(jiǎn)單且規(guī)則的數(shù)據(jù)流,。我們也致力于將流水線技術(shù)作為在硬件中實(shí)現(xiàn)這些算法的通用手段。借助于流水線技術(shù),，輸入和輸出之間的處理可以同時(shí)進(jìn)行,，因此，總的執(zhí)行時(shí)間變得最小,。在流水線的每一階段上,，采用流水線技術(shù)外加多處理技術(shù)能夠獲得最佳的性能。在下面，我們要論證一個(gè)微處理器陣列能夠借助流水線矩陣計(jì)算,，使得速度得到最佳的提升,。圖1是一個(gè)脈動(dòng)陣列的簡(jiǎn)單例子。在這種結(jié)構(gòu)下有兩個(gè)輸入向量陣列,，z和x,。處理單元有一個(gè)值，通常是根據(jù)定義在單元內(nèi)的運(yùn)算法則而得到的結(jié)果,。其輸出是一個(gè)向量,， 。

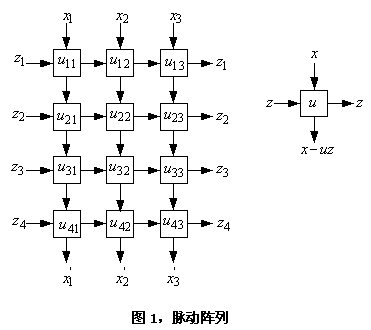
　　圖1中的脈動(dòng)陣列的輸出可以被簡(jiǎn)單地表示為向量矩陣關(guān)系：

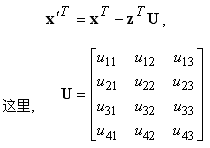
　　它顯示了如何采用一對(duì)

脈動(dòng)陣列來(lái)解決在很多信號(hào)處理情形 下出現(xiàn)的線性最小二乘問(wèn)題,。主陣列（三角形的）常用來(lái)實(shí)現(xiàn)Givens旋轉(zhuǎn)法 的流水線序列,，其通過(guò)歸一化變換到上三角形，從而減小數(shù)據(jù)矩陣 ,。
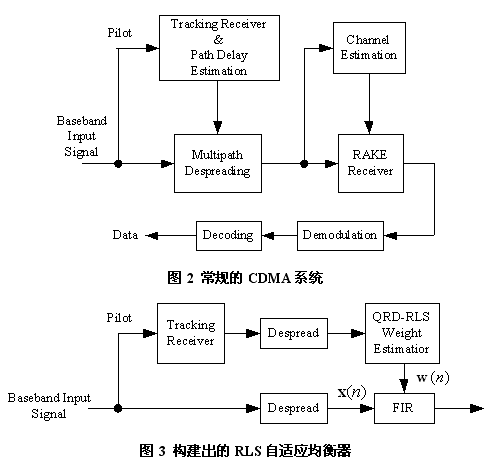
　　重要的實(shí)時(shí)應(yīng)用的數(shù)量在增長(zhǎng),，尤其在無(wú)線通信領(lǐng)域，要求系統(tǒng)在出現(xiàn)強(qiáng)干擾的情況下可靠地工作,?；诖a分多址（CDMA）技術(shù)的現(xiàn)代無(wú)線通信系統(tǒng)由于多路徑衰減、多址干擾（MAI）,、碼間干擾（ISI）這三個(gè)主要因素造成容量和性能上的限制,。克服這些困難的常用方案是采用發(fā)射功率控制,、錯(cuò)誤控制編碼以及典型地基于傳統(tǒng)耙狀接收機(jī)的多種技術(shù),。耙狀接收機(jī)的性能由于快速時(shí)變通道的出現(xiàn)而大打折扣，這些快速時(shí)變通道在實(shí)際的移動(dòng)無(wú)線通信系統(tǒng)中是很常見(jiàn)的,。有兩種干擾與用于CDMA下行線的耙狀接收機(jī)有關(guān)：一種是指間干擾（IFI）,；另一種是多址干擾（MAI）。這兩種干擾都是由于無(wú)線通道的頻率選擇引起的,。當(dāng)采用耙狀接收機(jī)時(shí),，IFI和MAI會(huì)使CDMA系統(tǒng)的容量受到限制。
　　改善CDMA傳輸?shù)男阅苄枰种艻FI和MAI,。當(dāng)延遲擴(kuò)散較大時(shí),，可以通過(guò)信道均衡，將頻率選擇性衰減信道轉(zhuǎn)換為頻率非選擇性衰減信道,。這樣,，基于自適應(yīng)規(guī)則的均衡接收機(jī)似乎是一個(gè)有效的CDMA接收機(jī)。它通過(guò)復(fù)原正交擴(kuò)頻碼來(lái)恢復(fù)發(fā)送的數(shù)據(jù),，從而抑制了IFI和MAI,。自適應(yīng)的最小均方（LMS）法和遞歸最小二乘（RLS）法迭代地計(jì)算時(shí)變信道,。借助相對(duì)較短的存放數(shù)據(jù)的緩沖器，它們具有較短的處理延時(shí)的優(yōu)點(diǎn),。RLS算法注重回溯到初始態(tài)的所有信息,，根據(jù)到達(dá)的新數(shù)據(jù)更新加權(quán)向量的估計(jì)值。由于收斂性較好,，因此RLS優(yōu)于LMS,。另外，如果自適應(yīng)算法發(fā)散,，或者收斂緩慢,，它將很難實(shí)現(xiàn)對(duì)IFI和MAI的抑制，而這是均衡接收機(jī)非?；镜哪繕?biāo),。另一方面，RLS算法需要在信號(hào)保持期間進(jìn)行大量的運(yùn)算,，而這不是一個(gè)實(shí)際的無(wú)線電系統(tǒng)所期望的,，因?yàn)楹?jiǎn)化是降低成本的關(guān)鍵所在。在改進(jìn)RLS濾波器的數(shù)字特性情形下,，引入通過(guò)QR分解（QRD）得到的輸入矩陣的直角三角形,。這樣的一個(gè)三角形化過(guò)程可以通過(guò)一系列的Givens旋轉(zhuǎn)法來(lái)實(shí)現(xiàn),，這種做法常被用來(lái)在基于樣本為單位的原理上實(shí)現(xiàn)QR的更新,。
　　采用Givens旋轉(zhuǎn)法的QRD-RLS算法的一種有效的并行三角形脈動(dòng)處理器陣列的實(shí)現(xiàn)方法已經(jīng)問(wèn)世 。一個(gè)統(tǒng)一的周期性時(shí)鐘控制著這個(gè)脈動(dòng)陣列,，它執(zhí)行平面旋轉(zhuǎn)以消除輸入信號(hào)矩陣的一些元素,。通常，旋轉(zhuǎn)角度的計(jì)算需要對(duì)開(kāi)方,、乘法和加法運(yùn)算求逆,。這種方法稱(chēng)作基本的Givens旋轉(zhuǎn)法，但存在自由的Givens平方根 ,。CORDIC算法也可以?xún)H僅采用二進(jìn)制的移位和加法來(lái)實(shí)現(xiàn),，但是由于需要定標(biāo)、更多的迭代以及計(jì)算中可能的不穩(wěn)點(diǎn)而增加成本,。圖2舉了一個(gè)常規(guī)的CDMA系統(tǒng)的例子,。作為比較，圖3展示了一個(gè)構(gòu)建出的RLS自適應(yīng)均衡器,。

 　　RLS的目的是在每個(gè)采樣時(shí)間 計(jì)算復(fù)數(shù)的權(quán)重向量,，從而減小殘值向量的模。

　　這里 是一個(gè)復(fù)數(shù)或觀測(cè)值,， 是想要得到的復(fù)數(shù)向量,，它要在同一時(shí)刻立即估計(jì)出來(lái),。包含在計(jì)算中、但沒(méi)有明確地表示出來(lái)的是一個(gè)指數(shù)型的權(quán)重因子（遺忘因子）,，它以累進(jìn)的方式極大地加權(quán)于舊的數(shù)據(jù)上,。這一加權(quán)可以通過(guò)優(yōu)于實(shí)際乘法運(yùn)算的二進(jìn)制移位方式來(lái)實(shí)現(xiàn)。在圖4中,，主三角形陣列ABC通過(guò)實(shí)行式（2）的QRD變換將數(shù)據(jù)矩陣 轉(zhuǎn)換為一個(gè)上三角形矩陣 ,。

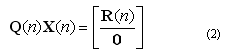
 是一個(gè)酉矩陣，它由一系列的Givens旋轉(zhuǎn)產(chǎn)生,。圖4中的圓形物體是旋轉(zhuǎn)（邊界）處理器單元,，方形物體是向量化（內(nèi)部）的處理器單元。旋轉(zhuǎn)單元計(jì)算適當(dāng)?shù)慕嵌刃D(zhuǎn)參數(shù),，并將它傳遞到向量化處理單元,。類(lèi)似的，在最小二乘處理器陣列單元的右列DE,，估計(jì)并存儲(chǔ)由式（3）所 定義的向量 ,。

　　優(yōu)化權(quán)重向量由式（4）給出。

　　每個(gè)旋轉(zhuǎn)和向量化處理單元都有一個(gè)定義過(guò)的算法來(lái)實(shí)現(xiàn)特定的系統(tǒng),，如圖1所示,。該系統(tǒng)可以有一個(gè)定義過(guò)的結(jié)構(gòu)來(lái)處理RLS或者經(jīng)過(guò)構(gòu)建來(lái)處理用于自適應(yīng)天線波束賦形技術(shù)中的最小方差無(wú)畸變響應(yīng)（MVDR）算法。注意圖4中的每個(gè)單元必須等到輸入向量 完全消失后才能更新它所存儲(chǔ)的數(shù)值,。這個(gè)過(guò)程也許理所當(dāng)然的是流水線式的,。需要牢記的是，當(dāng)處理復(fù)數(shù)時(shí),，旋轉(zhuǎn)首先必須使虛部為零,，然后再次旋轉(zhuǎn)使剩余的實(shí)部為零。注意單元的最后一列類(lèi)似傳統(tǒng)的耙狀接收機(jī)的一個(gè)接收分支,。

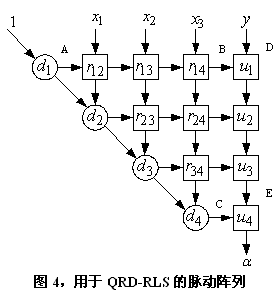
　　圖4中的脈動(dòng)陣列以高度的流水線方式運(yùn)行,。計(jì)算的波陣面以信號(hào)接收的速率傳播。在所要的信號(hào) 不可知的情況下,，采用"先驗(yàn)"的估計(jì)方法,。在此情形下， 反饋?zhàn)鳛?的輸入,。鑒于此反饋回路,，無(wú)法實(shí)現(xiàn)完全的流水線方式。然而,，處理陣列的列可以進(jìn)行流水線計(jì)算,，而行則不行。這樣的脈動(dòng)陣列實(shí)現(xiàn)方式的一個(gè)重要的潛在優(yōu)點(diǎn)是它的能效,。能耗在開(kāi)發(fā)用于無(wú)線系統(tǒng)的干擾抑制算法中至關(guān)重要,。在集成電路中,，能耗是門(mén)速度的遞增函數(shù) 。大的并行脈動(dòng)陣列處理方式能夠在不相應(yīng)地降低算法的更新速度的前提下,，使得單個(gè)門(mén)的速度大大下降,，這樣就達(dá)到了高能效的目的。

　　采用Givens旋轉(zhuǎn)的算法可以取得出色的數(shù)字性能,，它可以使用縮短字長(zhǎng)的算法有效地在ASIC和FPGA中實(shí)現(xiàn),。字長(zhǎng)必須足夠使權(quán)重的計(jì)算達(dá)到一定精度，從而徹底地消除干擾,。對(duì)于FPGA來(lái)說(shuō),，它的結(jié)構(gòu)需要針對(duì)字長(zhǎng)進(jìn)行參數(shù)化，并且要包含屬性以便提供布局信息,，從而在可預(yù)知時(shí)序的前提下,，實(shí)現(xiàn)非常密集的布局。
　　FPGA技術(shù)的發(fā)展速度令人震驚,。最新的FPGA提供了一種無(wú)需采用ASIC就可以達(dá)到自適應(yīng)系統(tǒng)所需的性能的方法,。例如DRAM，它們充分利用了當(dāng)今制造工藝所提供的大量晶體管,，它們能夠用來(lái)完成合適的并行運(yùn)算,。另外，諸如LatticeECP系列的FPGA現(xiàn)在已經(jīng)集成了DSP模塊,，可以用硬件方式實(shí)現(xiàn)乘法,、加法以及乘法累加（MAC）等功能。因此,，利用這種技術(shù)進(jìn)步和結(jié)構(gòu)優(yōu)化,，極有可能取得大大超越現(xiàn)有結(jié)構(gòu)的性能。