0 引言
傅立葉變換是一種將信號從時域轉(zhuǎn)變?yōu)轭l域表示的變換形式,它是數(shù)字信號處理中對信號進行分析時經(jīng)常采用的一種方法。信號的一些特性在時域總是表現(xiàn)得不明顯,通過傅里葉算法,將其變換到頻域,其特性就一目了然。例如,來自供電系統(tǒng)的干擾在時域上總是不易識別,但是在頻域上就可以很清晰地看到50~60 Hz的離散諧波。
在計算機系統(tǒng)中,實際上是以離散傅立葉變換(DFT)的方式處理數(shù)據(jù)。由于DFT的運算量比較大,并不適用于嵌入式控制系統(tǒng),所以實際應用中常使用DFT 的快速算法一快速傅立葉變換(FFT)。雖然FFT 比DFT的計算量減少了很多,但用普通單片機來實現(xiàn)FFT多點、實時運算還是比較困難的。DSP(數(shù)字信號處理器)具有運算速度快和精度高的特點,恰好滿足FFT的要求,能較好地解決這個問題。
1 快速傅里葉變換的原理
非周期性連續(xù)時間信號x(t)的傅里葉變換可以表示為
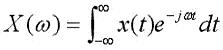
式中計算出來的是信號x(t)的連續(xù)頻譜。但是,在實際的控制系統(tǒng)中能夠得到的是連續(xù)信號x(t)的離散采樣值x(nT)。因此需要利用離散信號x(nT)來計算信號x(t)的頻譜。
有限長離散信號x(n),n=0,1,…,N-1的DFT定義為:
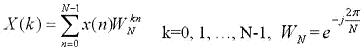
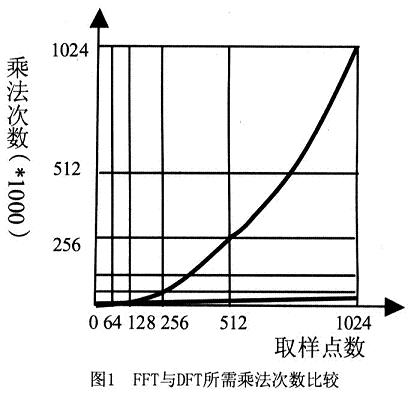
可以看出,DFT需要計算大約N2次乘法和N2次加法。當N較大時,這個計算量是很大的。利用WN的對稱性和周期性,將N點DFT分解為兩個N/2點的 DFT,這樣兩個N/2點DFT總的計算量只是原來的一半,即(N/2)2+(N/2)2=N2/2,這樣可以繼續(xù)分解下去,將N/2再分解為N/4點 DFT等。對于N=2m 點的DFT都可以分解為2點的DFT,這樣其計算量可以減少為(N/2)log2N次乘法和Nlog2N次加法。圖1為FFT與DFT-所需運算量與計算點數(shù)的關系曲線。由圖可以明顯看出FFT算法的優(yōu)越性。
將x(n)分解為偶數(shù)與奇數(shù)的兩個序列之和,即
![]()
x1(n)和x2(n)的長度都是N/2,x1(n)是偶數(shù)序列,x2(n)是奇數(shù)序列,則
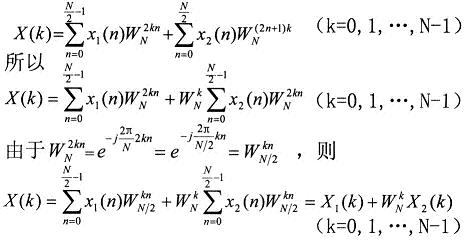
其中X1(k)和X2(k)分別為x1(n)和x2(n)的N/2點DFT。由于X1(k)和X2(k)均以N/2為周期,且WN k+N/2=-WN k,所以X(k)又可表示為:
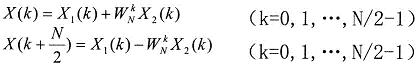
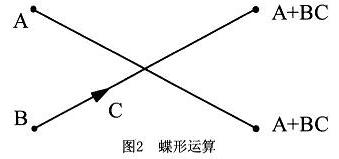
上式的運算可以用圖2表示,根據(jù)其形狀稱之為蝶形運算。依此類推,經(jīng)過m-1次分解,最后將N點DFT分解為N/2個兩點DFT。圖3為8點FFT的分解流程。
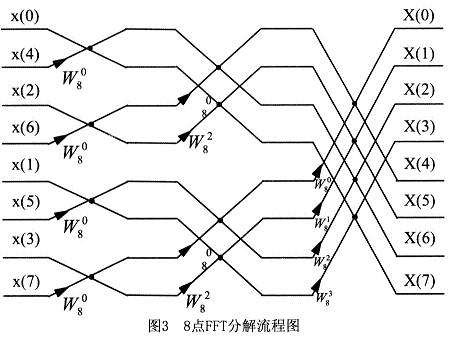
FFT算法的原理是通過許多小的更加容易進行的變換去實現(xiàn)大規(guī)模的變換,降低了運算要求,提高了與運算速度。FFT不是DFT的近似運算,它們完全是等效的。
2 快速傅里葉算法在TMS320LF2407上的實現(xiàn)
根據(jù)FFT算法的特點,處理器要在一個指令周期內(nèi)完成乘和累加的工作,因為復數(shù)運算要多次查表相乘才能實現(xiàn)。其二就是間接尋址,可以實現(xiàn)增/減1個變址量,方便各種查表方法。再次,F(xiàn)FT變換的輸入序列x(n)是按所謂的碼位倒序排列的,處理器要有反序間接尋址的能力。DSP控制器專門設計了特有的反序間接尋址,并能在一個指令周期內(nèi)完成乘和累加的運算。因此,對數(shù)字信號的分析處理,DSP比其它的處理器有絕對的優(yōu)勢。本文采用TI公司C2000系列TMS320LF2407芯片來實現(xiàn)FFT算法。
TMS320LF2407定點DSP是一款專為工業(yè)控制、電機控制和數(shù)字信號處理等用途而設計的DSP,具備單周期乘加指令,具有FFT反序間接尋址功能,最高運行速度為40MIPS。為了充分利用DSP芯片特有的反序間接尋址等功能,F(xiàn)FT算法程序采用匯編語言編寫,主程序采用C語言,因此程序具有良好的兼容性和可擴展性。
主程序流程圖如圖4所示。系統(tǒng)初始化主要完成DSP的系統(tǒng)控制和狀態(tài)寄存器、等待狀態(tài)發(fā)生器控制寄存器、中斷寄存器等的必要設置。
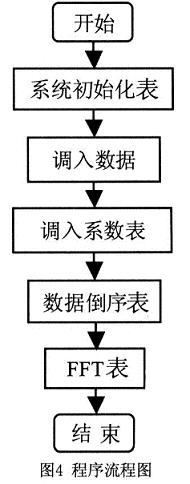
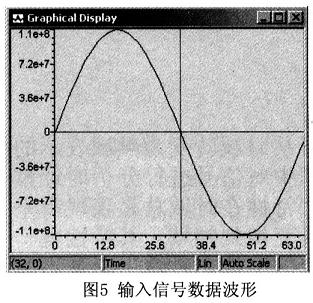
本程序采樣函數(shù)為:x=sin(20πt),采樣頻率為640Hz。
輸入數(shù)據(jù)波形如圖5所示。一般情況下,我們只關心信號頻域的幅度譜。幅度譜|X(k)|2的計算:X(k)=XR(k)+jX(k),|X(k)2|=|Xr(k)|2+|Xi(k)|2。FFT計算結(jié)果的信號幅度譜|X(k)|2如圖6所示。

輸入信號頻率是10Hz,根據(jù)公式f=kfs/N,f是原始信號的頻率,k表示峰值出現(xiàn)的位置,fS是采樣頻率,N是計算的點數(shù),從幅度譜中看出,峰值出現(xiàn)在k=1處,那么,f=1×640/64=10,與原始信號的實際頻率一致,說明計算結(jié)果正確。
3 快速傅里葉變換(FFT)的應用
FFT在生產(chǎn)實踐和科學研究中有著廣泛的應用。圖7為FFT的典型應用方案。下面簡單介紹一下FFT的應用領域。

(1)頻譜分析。對各類旋轉(zhuǎn)機械、電機、機床等機器的主體或部件進行實際運行狀態(tài)下的頻譜分析,可以提供設計數(shù)據(jù)和檢驗設計結(jié)果,或者找尋震源和診斷故障,保證設備的安全運行等。在聲納系統(tǒng)中,為了尋找海洋水面船只或潛艇,需要對噪聲信號進行頻譜分析,以提供有用信息,判斷艦艇運行速度、方向、位置、大小等。
(2)濾波。濾波是FFT最廣泛的應用,它使對波形的頻率分量濾波變得十分簡單。比如對采樣信號進行FFT后,去掉不需要的頻率分量,再進行FFT反變換,就得到濾波后的期望信號。
(3)電力監(jiān)控系統(tǒng)的諧波分析。電力監(jiān)控系統(tǒng)的諧波分析,需要對采樣數(shù)據(jù)進行FFT運算,然后通過液晶屏或其它人機界面重新繪畫出來,以方便技術(shù)人員掌握電力的質(zhì)量。
4 總結(jié)
實驗證明,此程序在TMS320LF2407定點DSP中運行良好,速度快且運算結(jié)果十分可靠,其用于一般的信號處理和工業(yè)控制都能滿足精度和實時的要求,具有較高的學術(shù)價值和良好的應用前景。其次,掌握FFT,學會在空域和頻域中同時思考問題,很多時候可以讓我們使用簡單的方法來解決復雜的問題。

