被譽為數(shù)學顯微鏡的小波變換是從傅里葉變換和加窗傅里葉變換發(fā)展而來的。小波變換引入伸縮和平移兩個參數(shù),，實現(xiàn)了時域－頻域局域化分析,，從而可以對圖像的任何局部區(qū)域進行多分辨率分析。由于小波變換后圖像具有高頻的方向選擇性,，與人眼的視覺特性相吻合,，人眼最重要的視覺特性是視覺掩蓋效應，即不變和有規(guī)則變化的區(qū)域很容易被遺忘,，而對突變和極不規(guī)則變化的區(qū)域感興趣。采用嵌入式零樹小波編碼及算法,，通過對感興趣的區(qū)域和不感興趣區(qū)域分別進行編碼,，可以達到充分利用信道資源和存儲空間、提高感興趣區(qū)域的圖像質量的目的,。
1 視覺掩蓋效應
　　在大多數(shù)應用場合,，最終的圖像總是由人眼來觀測的，但是人類的視覺系統(tǒng)并不完美,。通過對人眼視覺現(xiàn)象的觀察與研究發(fā)現(xiàn),，視覺掩蓋效應可以用于改善圖像信息的處理。
　　視覺選擇性與客體的特性有關,，人眼對空間頻率" title="空間頻率">空間頻率接近于零的平滑區(qū)域和空間頻率相似紋理區(qū)域有很大的鈍性,，所以不變與規(guī)則變化的場景很容易在人的意識中被遺忘，人類視覺通常只對突變和極不規(guī)則變化的區(qū)域感興趣,。這種與生俱來的選擇性使視覺只限定在有限的目標上,。
1.1 靜態(tài)對比靈敏度
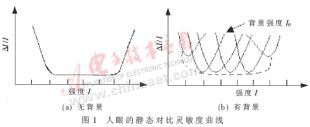
　　人眼主觀上可辨別的最小亮度差別所需要的最小光強差值稱為亮度的辨別閥值。也就是說,，當刺激光強I增大時,，最初感覺不出,，直到I變化到I+△I時人眼就感覺到亮度有變化了。人眼對亮度光強變化的響應是非線性的,，比值△I/I稱為對比靈敏度,。在相當寬的光強范圍內，△I/I保持常數(shù)為0.02,，但在I很低或很高時不是常數(shù),。如果有背景，則對比靈敏度不僅與目標物的光強度I有關,，而且與背景亮度I₀有關,。圖1給出了有背景和無背景時人眼的靜態(tài)對比靈敏度曲線。

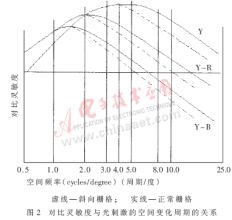
　　此外,，人眼的對比靈敏度還與刺激的空間變化周期(空間變化周期是指刺激的明暗不變,，只改變明暗的空間間隔)有關。如果亮度固定在一定水平下,，則對比靈敏度與光刺激的空間變化周期之間的關系如圖2所示,。這一關系通常被稱為人眼的調制傳遞函數(shù)。圖2中還給出了等亮度的色差信號Y－R和Y－B的對比靈敏度曲線,。由圖1和圖2可得到以下結論：
　　(1)恢復圖像的誤差如果低于對比靈敏度,，則不會被人眼覺察。
　　(2)高頻部分在相同的靈敏度閾值下,，色差信號Y－R的空間頻率只有亮度Y的一半,，Y－B則為Y的1/4，通常表示色差信號所需的像素比亮度要少得多,。
　　(3)在相同的靈敏度閾值下,，斜向柵格的空間頻率只有正常柵格的0.7，因此按斜向柵格對圖像數(shù)據(jù)采樣所需的頻率較低,。
　　(4)高頻端的靈敏度要小于低頻端,，因此對這些部分的量化誤差可大一些。
1.2 具有感興趣區(qū)域的人眼視覺特性
　　人們在觀察和理解圖像時常常不自覺地對其中某些區(qū)域產生興趣,，把這些區(qū)域稱為視覺感興趣區(qū)域,。整幅圖像的主觀視覺質量取決于感興趣區(qū)域的視覺質量，而不感興趣區(qū)域的降質常常不易被人覺察,，對整幅圖像視覺質量的影響較小,。例如對一副人像照片，反映一個人主要特征的是面部信息,，在進行圖像壓縮時,，人的面部信息與其它不重要的信息不必采用相同的壓縮比。顯然，感興趣區(qū)域的視覺特性也是一種視覺掩蓋效應,。
2 嵌入式零樹小波編碼及算法
2.1 EZW編碼
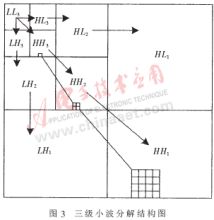
　　一幅圖像經過三級小波分解后形成十個子帶,，如圖3所示。小波系數(shù)的分布特點是越往低頻子帶,，系數(shù)值越大,，包含的圖像信息越多。如圖3中的LL3子帶,，越是高頻子帶,，系數(shù)值越小，包含的圖像信息越小,。在系數(shù)數(shù)值相同時,，低頻子帶反映圖像的低頻信息，對視覺比較重要,；而高頻子帶反映圖像的高頻信息,，對視覺不太重要。應選擇先傳輸較低頻系數(shù)的重要比特,，后傳輸較高頻系數(shù)的重要比特,。正是由于小波系數(shù)具有的這些特點，它非常適合于嵌入式編碼算法,。

　　嵌入式零樹小波編碼EZW(Embedded Zerotree Wavelet)方法是對整幅圖像進行同一級別編碼的方法,，圖像中的重要區(qū)域(感興趣區(qū)域)與背景區(qū)域(非感興趣區(qū)域)具有同樣的編碼級數(shù)。EZW編碼算法是一個簡單而有效的圖像編碼" title="圖像編碼">圖像編碼算法,，這種算法得到的比特流中的比特按其重要性排序,。使用這種算法，編碼者能夠在任一點結束編碼,，允許精確到任一個目標比特率或目標失真率,。
2.2 EZW算法
　　EZW算法利用小波系數(shù)的特點較好地實現(xiàn)了圖像編碼的嵌入功能，為了改善小波系數(shù)重要圖的壓縮,，定義了一個零數(shù)的數(shù)據(jù)結構,，即一個小波系數(shù)x,。對于一個給定的門限T,，如果|x|＜T，則稱小波系數(shù)x是不重要的,。如果一個小波系數(shù)在一個粗尺度上,，關于給定的門限是不重要的，且之后在較細的尺度上,，對同樣空間位置中的所有小波系數(shù)關于給定的門限T也是不重要的,，則稱小波系數(shù)形成了一個零數(shù)。這時,，在粗尺度上的那個小波系數(shù)稱為母代小波系數(shù),，它是樹根,，在較細尺度相應位置上的小波系數(shù)稱為子代小波系數(shù)。如果一個小波系數(shù)關于門限T是不重要的,，但它的子代小波系數(shù)中關于門限T是重要的系數(shù),，則稱這個小波系數(shù)是孤立零。因此,，小波系數(shù)有三種情況：零數(shù)根(ZTR),、孤立零(IZ)、重要系數(shù),。當然,，為了編碼的需要還可把重要系數(shù)分為正重要系數(shù)(POS)和負重要系數(shù)(NEG)。
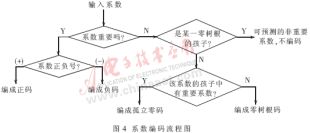
　　對于一個圖像的數(shù)據(jù)流,，圖4給出了一個系數(shù)編碼的流程圖,。

3 具有感興趣區(qū)域的靜止圖像壓縮編碼算法研究
3.1 EZW_ROI編碼算法
　　為了提高感興趣區(qū)域的圖像質量，在信道資源和存儲空間有限的條件下,，提出感興趣區(qū)域的零樹編碼算法EZW_ROI(Embedded Zerotree Wavelet with Region of interests),，它對感興趣區(qū)域圖像和背景圖像采用不同的壓縮步驟，使感興趣區(qū)域內的圖像比背景圖像具有更好的圖像質量,。
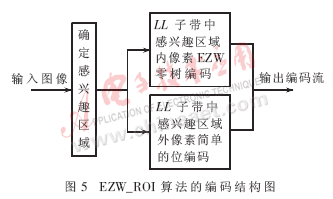
　　對感興趣區(qū)域內外的圖像采用不同的零數(shù)小波編碼,。整個編碼算法分三步進行：
　　(1)確定感興趣區(qū)域：人像照片可以把感興趣區(qū)域確定為面部區(qū)域。在視頻監(jiān)視系統(tǒng)中,，可以把監(jiān)視環(huán)境中的重要場景設為感興趣區(qū)域,。
　　(2)對低頻子帶中感興趣區(qū)域內的系數(shù)進行編碼：即對感興趣區(qū)域內的圖像進行編碼，系數(shù)采用EZW算法的零樹結構,，按照EZW算法的思想進行零樹掃描和編碼,。
　　(3)對低頻子帶中不在感興趣區(qū)域內的系數(shù)進行編碼：即對背景區(qū)域的圖像進行編碼，系數(shù)的編碼不用EZW算法的零樹結構,，只對背景區(qū)域的低頻信息進行編碼,。
　　圖5是EZW_ROI算法的編碼結構框圖。

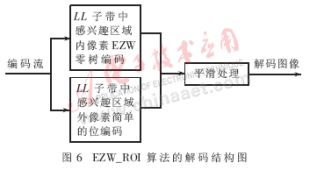
3.2 EZW_ROI解碼算法
　　對編碼圖像進行解碼時,，與編碼過程相反,，也分三步進行：
　　(1)對低頻子帶中的感興趣區(qū)域內圖像進行與EZW算法同樣的零樹編碼。
　　(2)對低頻子帶中的感興趣區(qū)域外圖像進行簡單的位解碼,。
　　(3)消除邊緣效應：在以上兩步的基礎上,，對感興趣區(qū)域的四周做3×3的均值濾波，以消除感興趣區(qū)域邊緣的影響,，使得感興趣區(qū)域外的圖像在視覺上差別變弱,。
　　圖6 是EZW_ROI算法的解碼結構框圖。

4 應用實例
　　在研究中采用了一幅標準的8bpp的灰度人像，首先,，確定感興趣區(qū)域為人像的面部,，對原始圖像進行四級的小波分解，小波變換采用S+P變換,；最后對圖像進行32倍壓縮,，即壓縮后的比特率為0.25bpp。用EZW算法和EZW_ROI算法恢復的圖像如圖7所示,。在信道資源和存儲空間有限的條件下,，為了提高感興趣區(qū)域的圖像質量，采用具有感興趣區(qū)域的圖像壓縮方式,，對感興趣區(qū)域圖像和背景圖像采用不同的壓縮步驟,，使圖像中的重要信息盡可能少損失。試驗證明,，在高壓縮比的情況下,，EZW_ROI算法的重建圖像比EZW算法的重建圖像具有更好的視覺效果。