小波圖像編碼和分形圖像編碼是兩種不同的圖像編碼方法,，二者各有其特點(diǎn)，又都存在一定的局限性[1-3],。一幅圖像經(jīng)過小波變換后,，其相同方向但不同分辨率的子圖像具有較強(qiáng)的相似性，這種相似性正好與分形編碼的特點(diǎn)具有互補(bǔ)性,。自1995年以來,，Rinaldo和Calvagno首次提出并實(shí)現(xiàn)了一種小波與分形圖像編碼相結(jié)合的算法[4]。此后,，又出現(xiàn)多種小波變換與分形相結(jié)合的圖像編碼算法[5-8],。這些算法，有的證明了小波域的分形圖像解碼可以通過低分辨率小波系數(shù)向高分辨率系數(shù)連續(xù)外推實(shí)現(xiàn),，即解碼無需循環(huán)迭代,，是無條件收斂的；有的通過采用平滑小波基消除重構(gòu)圖像在高壓縮比時(shí)的方塊效應(yīng),；有的推導(dǎo)出仿射變換的收縮因子取值不受限制,，能保證解碼收斂；同時(shí)小波系數(shù)的樹狀結(jié)構(gòu)提供了自然高效的Domain塊分類方法等[9],。此外,，還有一些研究集中在分形塊的類別劃分[10]以及基于小波零樹結(jié)構(gòu)的分形預(yù)測[11]等。
    本文在此基礎(chǔ)上,，通過分析基本分形圖像編碼的壓縮算法,，提出一種基于小波域的分形圖像編碼改進(jìn)算法,。這種改進(jìn)算法包括兩部分：(1)根據(jù)圖像小波分解后各子圖像包含的不同能量，考慮各子圖像所代表的方向,、紋理特征等信息,，對各子圖采用非均勻的分形編碼方案，即在進(jìn)行小波域的分形編碼時(shí),，分形塊的選取不一定全是正方形,，對于不同方向的紋理特征的小波子圖像選取不同形狀的分形塊； (2)根據(jù)圖像的小波變換系數(shù)在同一方向不同分辨率,、同一分辨率不同方向之間都存在相關(guān)性,，對每一圖像塊，在同一方向低一級分辨率的子帶圖像上尋找與其最佳分形匹配的相似塊,，由這些相似塊形成一棵一棵預(yù)測樹,，解碼端通過對預(yù)測樹的分形預(yù)測恢復(fù)出各級圖像塊。實(shí)驗(yàn)證明,，這種改進(jìn)算法能夠大大提高分形編碼的速度,，并取得較高的壓縮比。
1 基本分形編碼壓縮算法
　　基本分形編碼壓縮算法的主要內(nèi)容：將待編碼的圖像分割成互不重疊的子塊(Range Block),稱為圖像塊R,，同時(shí)將圖像分割成可以相互重疊的大一些的塊(Domain Block),，稱為相似塊D。對分割后的R塊和D塊進(jìn)行分類,，如：變換平緩的平滑區(qū)域、變換突然的邊緣區(qū)域和變換緩和的中間型區(qū)域等,，使相匹配的塊具有相同的區(qū)域性質(zhì),。對分類后相同區(qū)域的每一個(gè)R塊Rj尋找可以匹配的D塊Dj，使得Dj通過仿射函數(shù)ψ_j可以近似于R_j,，由此可以得到一組仿射變換組ψ₁,，ψ₂…ψ_N，即分形迭代系統(tǒng),。只要該系統(tǒng)的變換是收斂的,，且比原系統(tǒng)簡單，就實(shí)現(xiàn)了分形壓縮[12],?；痉中尉幋a算法主要在圖像分割后對R塊和D塊進(jìn)行搜索匹配的過程，其壓縮比較高,，但是壓縮時(shí)的計(jì)算量較大,，編碼壓縮時(shí)間很長。
2 基于小波域的分形圖像編碼改進(jìn)算法
    本文的改進(jìn)算法包括兩部分：小波域分形編碼過程中分形塊形狀的選取以及分形預(yù)測樹的形成,。
2.1 小波域分形編碼過程中分形塊形狀的選取
    在上述基本分形壓縮編碼過程中,，在確定R塊和D塊的形狀時(shí)，對各小波分解子圖取的均是正方形。由于圖像小波分解后,，各子圖包含的能量有所不同,，其代表的方向、紋理等特征信息也不相同,，因此,，可以考慮在進(jìn)行小波域的分形編碼時(shí),分形塊的選取可以不選正方形，而是依據(jù)小波分解子圖的不同方向的紋理特征選取不同形狀的子塊,。
　以512×512的8 bit圖1為例進(jìn)行實(shí)驗(yàn),，計(jì)算結(jié)果表明，不同方向的子圖由于其紋理特征信息不同,，在LH,、HL、HH區(qū)域中,其水平和垂直方向的相關(guān)性不相同,，所以在不同方向的分解子圖像中采用不同形狀的塊進(jìn)行分形編碼,，可使其編碼時(shí)間更短，圖像恢復(fù)效果更好,。例如,，在LH區(qū)域，通過計(jì)算分析,，行相關(guān)長度大于列相關(guān)長度,，圖像以水平紋理為主，可采用4×2的矩形進(jìn)行R塊和D塊的分割,；在HL區(qū)域,，行相關(guān)長度小于列相關(guān)長度，圖像以豎直紋理為主,，可采用2×4的矩形進(jìn)行R塊和D塊的分割,；而在HH區(qū)域，行相關(guān)長度與列相關(guān)長度接近,，則可以采用正方形來分割,。同時(shí)，由于左上角的低頻子圖包含了圖像的大部分能量,，因此仍采用2×2正方形子塊的選取,，不參加計(jì)算。圖像塊的分割方法如圖2所示,。應(yīng)用均勻分塊和非均勻分塊的壓縮效果比較如圖3 所示,。

2.2 分形預(yù)測樹的形成過程
    分形預(yù)測樹的形成原理是:應(yīng)用Davis把零樹的概念引入到分形圖像編碼的理論，把分形圖像編碼中的相似塊和圖像塊擴(kuò)大到相似樹(Domain Tree)和圖像樹(Range Tree),從而使得相似塊與圖像塊之間的分形匹配轉(zhuǎn)化為相似樹與圖像樹之間的分形匹配,。在此基礎(chǔ)上,，可以在各級小波分解的子圖像中尋找與圖像塊R最佳分形匹配的代表塊,，再由各級代表塊按照零樹結(jié)構(gòu)產(chǎn)生一棵代表樹，通過計(jì)算比較各級圖像樹R與代表樹的距離,，確定距離最小的代表樹就是圖像樹R的預(yù)測樹,。
　結(jié)合小波域圖像分割形狀的分析，對圖1進(jìn)行如圖2所示的小波域分割,，得到基于小波域的分形預(yù)測樹的形成圖如圖4 所示,。具體過程是：

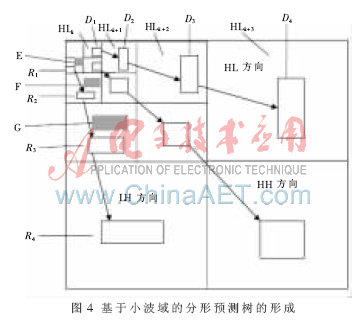
    (1) 首先對圖像進(jìn)行多次小波變換，產(chǎn)生各個(gè)子帶圖像,。通過對圖像行,、列相關(guān)性的計(jì)算分析，確定各子帶小波域圖像分割的形狀,。為了保證信噪比,，對最低分辨率的子帶圖像LL1、HL1,、LH1,、HH1不編碼。
    (2) 同時(shí)在水平,、垂直,、對角線3個(gè)方向上形成一棵一棵圖像樹，即零樹,。如LH方向上的R=(R₁,，R₂，R₃,，R₄）就是其中一棵圖像樹,，而D=(D₁，D₂,，D₃，D₄)表示HL方向上的相似樹,。然后在LH1中尋找與圖像塊R2最佳分形匹配的代表塊E1,，再由E1按照零樹結(jié)構(gòu)產(chǎn)生一棵代表樹E=(E₁，E₂,，E₃),。同理，在LH2中尋找與圖像塊R3最佳分形匹配的代表塊F₂,，并生成代表樹F=(F₁,，F(xiàn)₂，F(xiàn)₃),。在LH3中尋找與圖像塊R4最佳分形匹配的代表塊G3,，并生成代表樹G=(G₁,，G₂，G₃),。
    (3)分別計(jì)算圖像樹R與3棵代表樹E,、F、G的距離,，距離最小的代表樹就是圖像樹R的預(yù)測樹,。然后將預(yù)測樹在相應(yīng)層次的位置以及經(jīng)歷的幾何變換和仿射變換作為圖像樹R的分形預(yù)測編碼。
    (4) HL,、HH方向按同樣方式編碼,只是構(gòu)成的R塊和D塊的形狀大小不同,。這樣，在改進(jìn)算法中,編碼只需對代表樹中的一個(gè)代表塊進(jìn)行分形編碼,。而解碼時(shí),，又可依據(jù)這個(gè)代表塊通過零樹結(jié)構(gòu)推出其他代表塊，再分形預(yù)測圖像塊R,。
    由于前面針對小波分解圖的能量分配特性已經(jīng)采用了非均勻的分形塊形狀的選取,，再結(jié)合這種分形預(yù)測編碼方法，其結(jié)果大大提高了分形編碼的速度,，縮短了編碼時(shí)間,，在提高壓縮比方面也取得了良好的效果。
3 實(shí)驗(yàn)結(jié)果
　實(shí)驗(yàn)采用圖1所示圖像,，分別用基本分形編碼方法和本文的改進(jìn)算法進(jìn)行實(shí)驗(yàn),，其重建圖像如圖5所示?；痉中尉幋a時(shí)各子圖中圖像塊大小為4×4,，相似塊大小為8×8，改進(jìn)算法中對小波分解圖像塊的分割方法如圖2所示,，相似塊大小取為圖像塊大小的2×2倍,，實(shí)驗(yàn)結(jié)果如表1所示。

　本文提出基于小波域的分形圖像編碼改進(jìn)算法是將小波域分形與分形預(yù)測方法相結(jié)合,，由表1可知,，與基本分形算法相比，在恢復(fù)圖像質(zhì)量接近的情況下,，壓縮比提高約2倍,，信噪比下降2 dB，而編碼時(shí)間大大縮短,，提高了編碼速度,，表明在提高壓縮比方面，效果良好,。
參考文獻(xiàn)
[1]  余松煜,，張文軍,，孫軍.現(xiàn)代圖像信息壓縮技術(shù)[Ml.北京:科學(xué)出版社，1998.
[2]  陳守吉,，張立明.分形與圖像壓縮[M].上海：上?？萍冀逃霭嫔纾?998.
[3]  BRENDT W,，GERHARD D J. A review of the fractal image coding literature[J]. IEEE Transactions on Image  Processing, 1999, 8(12):1716-1729.
[4]  RINALDO R, CALVAGNO G. Image coding by block  prediction of multiresolution subimages[J]. IEEE Transaction On    Image Processing ,1995, IP-4(7):909-920.
[5]  DAVIS G. A wavelet-based analysis of fractal image compression[J]. IEEE Transactions on Image Processing, 1998,7(2):141-154.
[6]  DAVIS G. Adaptive self-quantization of wavelet subtrees: a wavelet-based theory of fractal images compression[C]. SPIE Conf. on Mathematical Imaging: Wavelet application in Signal and Image Processing, San Diego:1995:265-279.
[7]  WALLE A V D. Merging fractal image compression and  wavelet transform methods[C]. In Fractal Image Coding  Analysis: A NATO Series Book, Yuval Fisher, Ed. New  York: Springer Verlag,1996:523-597.
[8]  KRUPNIK H, MALAH D, KARNIN E. Fractal representation of images via the discrete wavelet transform[C]. In  IEEE 18th Conference of  EE, Israel: 1995,3:187-191.
[9]  張宗念,，馬義德，余英林.基于方向性零樹小波的分形圖像編碼[J]．電子科學(xué)學(xué)刊,，2000,，22(5):780-783.
[10] 周艷， 吳敏金.基于方向剖分的小波域分形圖像壓縮[J]．華東師范大學(xué)學(xué)報(bào)（自然科學(xué)版）,，2002,，3(9)：20-23.
[11]  謝鑫，馬爭鳴.基于小波系數(shù)零樹結(jié)構(gòu)的分形預(yù)測圖像編碼[J].中國圖像圖形學(xué)報(bào),，2000,，5（11）：920-924.
[12]  JACQUIN A E. Fractal image coding: A Review[J]. Proc.     of IEEE, 1993, 81(10):1451-1465.