引言
    現(xiàn)代雷達普遍采用相參信號來進行處理,，而如何獲得高精度基帶數(shù)字正交(I，Q)信號是整個系統(tǒng)信號處理成敗的關(guān)鍵,。傳統(tǒng)的做法是采用模擬相位檢波器來得到I,、Q信號，其正交性能一般為：幅度平衡在2％左右,，相位正交誤差在2°左右,，即幅相誤差引入的鏡像功率在-34 dB左右。這樣的技術(shù)性能限制了信號處理器性能的提高,。為此,，近年來提出了對低中頻直接采樣恢復(fù)I、Q信號的數(shù)字相位檢波器,。隨著高位,、高速A／D的普遍應(yīng)用，數(shù)字相位檢波方法的實現(xiàn)已成為可能,。

  本文介紹了一種正交相干檢波方法,，并給出了其FPGA的實現(xiàn)方案。

1 基本原理
1．1 中頻信號分解的基本原理
    一個帶通信號通?？杀硎緸椋?br />
    其中,，xI(t),、xQ(t)分別是s(t)的同相分量和正交分量。ω0為載頻,，a (t),、φ(t)分別為包絡(luò)和相位。它們之間具有如下關(guān)系：
   
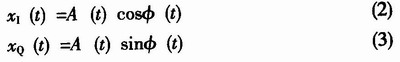
    所構(gòu)成的復(fù)包絡(luò)信號為,，該信號包含了式(1)中的所有信息,。
    要對中頻信號進行直接采樣，首先要保證采樣后的頻譜不發(fā)生混疊,。根據(jù)基本的采樣理論,，即Nvquist采樣定理要求以不低于信號最高頻率兩倍的采樣速率對信號直接采樣，才能保證所得到的離散采樣值能夠準確地確定信號,。然而,，如果信號的頻率分布在某一有限頻帶上，而且信號的最高頻率fH遠大于信號的帶寬,，那么,，此時若仍按Nyquist采樣率來采樣，則其采樣頻率就會很高,，以致難以實現(xiàn),，或是后續(xù)處理的速度不能滿足要求。因此,，此時就要用到帶通采樣理論,。
    所謂帶通采樣定理，即設(shè)一個頻率帶限信號選x(t),，其頻帶限制在(fL,，fH)內(nèi)，此時,，如果其采樣速率滿足：
   
    式中,，n取能滿足fs≥2(fH-fL)的最大正整數(shù)(O，1,，2,，……)，則用fs進行等間隔采樣所得到的信號采樣值就能準確地確定原始信號,。
    式(4)中的fs用帶通中心頻率f0和頻帶寬度B可表示為：
   
    其中,，，n為整數(shù),，且要求滿足fs≥2B,，B為信號帶寬。
    值得指出的是,，上述帶通采樣定理適用的前提條件是：只允許在其中的一個頻帶上存在信號,，而不允許在不同的頻帶上同時存在信號,，否則將會引起信號混疊。
1．2 Bessel插值法基本原理
    設(shè)A／D變換輸入的窄帶中頻信號為：
   
    式中,，A(t)為幅度,，f0為中頻頻率，φ(t)為初相,，τ為回波脈沖寬度,。
    假設(shè)式(5)中n=2，則采樣頻率,。事實上,，若對窄帶中頻信號采樣，則第N個采樣點離散形式為：
   
    式中,，為采樣間隔,。

另外，由貝塞爾內(nèi)插公式知,，其8點中值公式為：
   
    式中,，I2、I4,、I6,、I8為已知點，為,，I2,、I4、I6,、I8的中值點,。
    在實際應(yīng)用中，考慮到FPGA的特性,，可將
    (8)式改寫成以下形式：
   
    這樣，對于下列時間序列：Q1,、I2,、Q3、I4,、Q5,、I6、Q7,、I8,，按式(9)即可求出，而Q5即為兩組正交信號,。由此就可得到內(nèi)插運算的原理框圖如圖1所示,。

2 基于FPGA的實現(xiàn)方案
    首先將輸入FPGA的一路12位數(shù)字信號中的每一位都與時鐘信號進行異或運算,，以使I’(n)=x(2n)(-1)n和Q’(n)=x(2n+1)(-1)n+1，從而達到符號修正的目的,。經(jīng)過修正,，輸出的數(shù)字信號序列是一個由I的偶數(shù)項和Q的奇數(shù)項交替出現(xiàn)所組成的序列，即：I0,，Q1,，I2，Q3,，I4,，Q5，…,，I2n,，Q2n+1…。為實現(xiàn)Bessel插值,，還需要得到某時刻Q2n+1值所對應(yīng)的I的偶數(shù)項(I2n-2,，I2n，I2n+2和I2n+4),。鑒于移位寄存器有延時功能,，可使用12片移位寄存器74164取出I的偶數(shù)項序列，同時分離的還有相應(yīng)的Q2n+1一路信號,。接著,，I的偶數(shù)項序列經(jīng)過加法器電路進行有符號加、減法運算,。由于Bessel插值中的分母均為2的整數(shù)冪,，因而用右移來實現(xiàn)2的整數(shù)冪除法非常方便。其實現(xiàn)框圖如圖2所示,。

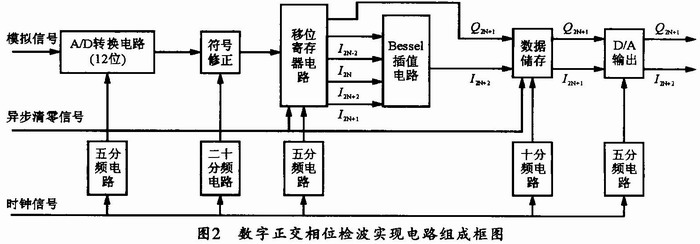
    該FPGA實現(xiàn)方法,，由于只涉及移位、簡單門和加減法運算,，因此,，用FPGA實現(xiàn)起來很方便，也可以獲得較高的運算速率,。

3 基于FPGA的硬件仿真結(jié)果
    為便于觀察,，仿真時可設(shè)定輸入信號A (t)為常數(shù)，A／D的采樣率fs為8 MHz來對信號進行中頻采樣并插值,，以得到二路正交信號,。運用QuartusⅡ的仿真結(jié)果如圖3所示。

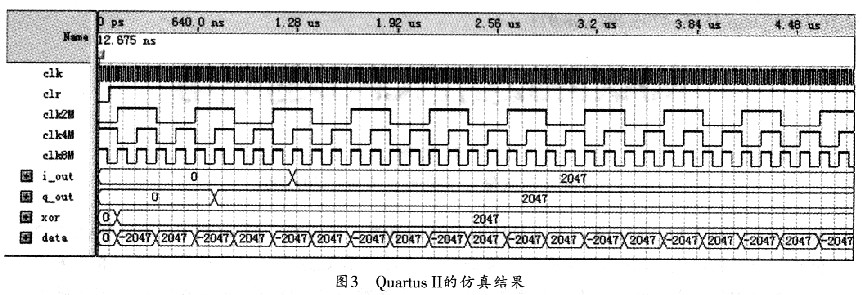
    圖3中，data為A／D采樣后的輸入信號,，xor為符號修正后的信號,，i_out，q_out為輸出信號,。
    之后,，將仿真程序下載到電路板中的FPGA(使用的是ALTERA公司的EPlC3T144C7芯片)中，便可用示波器觀察到如圖4所示的仿真結(jié)果,。

    從圖4可以看出,，I，Q兩路輸出為相似的波形,，符合前面的設(shè)定A(t)為常數(shù),；其中圖4(a)為圖4(b)的展開圖，由圖4可以看出,，I,，Q兩路
信號存在相位上的差異。

4 結(jié)束語
    本文詳細介紹了中頻直接正交采樣及Bessel插值理論,，并基于這一理論,，用FPGA將一路中頻信號分解成了兩路正交數(shù)字信號，本文同時重點給出了用FPGA實現(xiàn)這一過程的詳細方案,。