摘 要: 提出了一種基于非抽樣Contourlet變換的紅外圖像增強算法,利用非線性函數(shù)對紅外圖像Contourlet變換系數(shù)進行修正,以增強圖像有益貢獻的同時抑制噪聲分量。實驗表明,與傳統(tǒng)的圖像增強算法相比,該算法可以有效地增強紅外圖像的細(xì)節(jié)和紋理。
關(guān)鍵詞: 紅外圖像增強; 非抽樣Contourlet變換; 非線性函數(shù)
隨著紅外技術(shù)的迅速發(fā)展,它已廣泛應(yīng)用于軍事國防、遙感探測、無損檢測等眾多領(lǐng)域。由于紅外圖像的成像機理以及紅外成像系統(tǒng)自身的原因,紅外成像系統(tǒng)的成像效果不夠理想,大多紅外圖像都有對比度低、圖像模糊、灰度范圍窄的缺點。實際應(yīng)用中,為了提高紅外圖像的質(zhì)量,需要對紅外圖像進行必要的增強處理。一般圖像增強處理的方法是基于空間域和變換域的,前者主要包括直接灰度變換、空間濾波和直方圖處理等;后者是將圖像由時域變換到頻域,再通過修正變換域內(nèi)的系數(shù)達到增強圖像的目的,它優(yōu)于基于空間域的增強方法,代表性算法有小波變換的算法和基于Contourlet變換的算法等[1]。
2002年,DO和VETTERLI提出的Contourlet變換是多尺度幾何分析方法中十分重要的一類。Contourlet能夠?qū)崿F(xiàn)一種“真正”二維的圖像表示,能夠提取在圖像中非常重要的內(nèi)在幾何結(jié)構(gòu)特征。類似于小波可以從濾波器角度考慮,Contourlet則利用不可分的濾波器建立了一個離散的多分辨率多方向率分析,實現(xiàn)靈活的多分辨率、局部的、具有方向性的圖像表示。研究Contourlet變換的方向選擇能力和非線性近似能力,體現(xiàn)Contourlet變換超越小波的優(yōu)異表現(xiàn)。但是由于小波變換與Contourlet變換都缺乏平移不變性,圖像增強結(jié)果會產(chǎn)生偽Gibbs失真,CUNHA A L等提出的非抽樣Contourlet變換具有平移不變性,可以在一定程度上抑制這種失真。本文對其進行了改進,與基于小波變換、Contourlet變換的圖像增強算法相比,該算取得了良好的增強效果[2]。
1 非抽樣Contourlet變換
Contourlet變換也稱金字塔形方向濾波器組PDFB(Pyramidal Direction Filter Bank),其分解變換的實現(xiàn)可以分為兩個步驟:拉普拉斯金字塔LP(Laplacian Pyramid)分解和方向濾波器組DFB(Directional Filter Bank)濾波。其變換思想是使用類似于線段的基函數(shù)去逼近原始圖像,從而實現(xiàn)對圖像信號的稀疏分離。因此,要實現(xiàn)Contourlet變換,首先需要對圖像進行一個多尺度變換以檢測不同尺度下的奇異點,然后再通過一個具有局部性的方向變換將同一尺度下相鄰的奇異點連接成線段結(jié)構(gòu)[3]。Contourlet變換的實現(xiàn)過程可以歸納為如下步驟:
(1)使圖像通過類似于小波的多尺度變換以檢測邊緣上的奇異點;
(2)將步驟(1)所得到的圖像通過局部化的方向變換完成輪廓線段的檢測。
非抽樣Contourlet變換NSCT(Nonsubsampled Contourlet Transform)由非抽樣塔狀濾波器NSP(Nonsubsampled Pyramid)將圖像分解為低頻部分和高頻部分,然后由非抽樣方向性濾波器組NSDFB(Nonsubasmpled Directional Filter Banks)將高頻部分分解為若干個方向。
NSP是一種平移不變性的雙通道濾波器結(jié)構(gòu),它使NSCT具有多尺度性質(zhì),并且下一層次的濾波器可以通過對上一層的濾波器抽樣得到。其頻域分解圖如圖1所示。

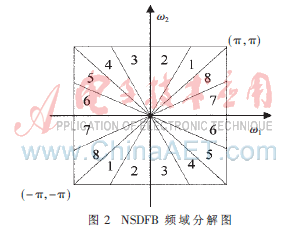
NSDFB由兩通道的非采樣濾波器組迭代構(gòu)成,該濾波器組也沒有進行采樣,具有平移不變性。NSDFB可以將第一級變換所得到的高頻部分分解為2的任意次冪個方向,每個方向上的高頻部分與NSP得到的低頻部分以及原始圖像都有相同的大小。NSDFB分解是將信號在一組基函數(shù)上展開,它對應(yīng)的基函數(shù)之間是冗余的[4]。頻域分解圖如圖2所示。
NSP與NDFB可以保證信號完全重建的條件是濾波器必須滿足等式:

其中,H0(z)、H1(z)表示分解濾波器,G0(z)、G1(z)表示重建濾波器。非抽樣Contourlet變換在表達圖像時具有Contourlet變換所具有的優(yōu)點,還具有平移不變性[4]。
2 基于的非抽樣的Contourlet變換圖像增強算法
圖像變換后,對變換系數(shù)分三種:強邊緣、弱邊緣和噪聲。強邊緣每個方向的系數(shù)值都較大;弱邊緣在某一方向的系數(shù)大,但在其他方向上的系數(shù)小;噪聲是指那些在所有方向上的系數(shù)都較小[5]。LAINE A F提出的增強函數(shù):

x為輸入原始圖像的變換系數(shù),0<p<1再次放大。此函數(shù)可以放大弱邊緣的系數(shù),保持強邊緣的系數(shù)[6]。
基于Contourlet變換的圖像增強算法的流程如圖3所示,具體步驟如下:
(1)對圖像進行非抽樣Coutourlet變換,得到不同尺度不同方向的變換系數(shù);
(2)按照上述原則對Contourlet變換系數(shù)進行處理;
(3)由修正后的變換系數(shù)重建增強圖像。

3 實驗結(jié)果與分析
本文采用客觀評價標(biāo)準(zhǔn)信噪比SNR來衡量不同去噪方法去噪后圖像的客觀質(zhì)量,SNR的定義如下:
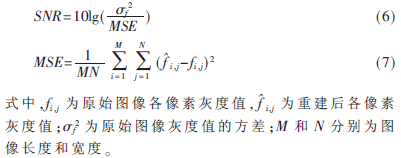
實驗結(jié)果如圖4所示。原圖是分辨率為640×480像素的紅外熱像儀拍攝的紅外照片,建筑物為主要探測目標(biāo),建筑物后有少量植被。圖4(b)為加噪圖像,圖4(c)為利用拉普拉斯變換處理的圖像,圖4(d)為利用Contourlet變換處理的圖像,圖4(e)為利用本文算法處理的圖像。SNR值如表1所示。


由表1可知,本文算法的SNR明顯提高,圖像視覺也更好,符合真實情況。Contourlet變換方法能夠抓住圖像幾何本質(zhì)特征,在表現(xiàn)各項異性的奇異性時性能更加優(yōu)越,因此處理紋理信息豐富的圖像效果更好。
參考文獻
[1] ESLAMI R, RADHA H. Wavelet based contourlet coding using an SPIHT-like algorithm[C].Singapore:IEEE International Conference on Image Processing,2004.
[2] ESLAMI R, RADHA H. The contourlet transform for image de-noising using cycle spinning[C]. Pacific Grove,USA: Asilomar Conference on Signals, Systems and Computers, 2003:1982-1986.
[3] DO M N, VETTERLI M. The contourlet transform: an efficient directional multiresolution image representation[J]. IEEE Trans on Image Processing, 2005,14(12):2091-2106.
[4] SERRA J. Image analysis and mathematical morphology VolumeI: theoretical advances [M].London:Academic,1988.
[5] NEZHADARYA E, SHAMSOLLAHI M B. Image contrast enhancement by cotourlet transform[C]. 48th International Sym Posium EIMAR,Zadar,Croatia,2006.
[6] 梁棟,沈敏.一種基于Contourlet遞歸Cycle Spinning的圖像去噪方法[J].電子學(xué)報,2005,33(11):2044-2046.

