乘法器被廣泛應(yīng)用于各種數(shù)字電路系統(tǒng)中,，如DSP、數(shù)字圖像處理等系統(tǒng),。隨著便攜電予設(shè)備的普及,，系統(tǒng)的集成度越來越高，這也對產(chǎn)品的功耗及芯片的散熱提出了更高的要求,。本文提出了一種新的編碼算法,，通過這種算法實(shí)現(xiàn)的乘法器可以進(jìn)一步降低功耗，從而降低整個(gè)電子系統(tǒng)的功耗,。

1 乘法器結(jié)構(gòu)
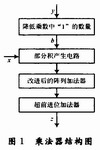
    本文介紹的24×24位乘法器的基本結(jié)構(gòu)如圖1所示,。其中，“降低乘數(shù)中‘1’的數(shù)量”實(shí)現(xiàn)對乘數(shù)y的編碼,，以降低乘數(shù)y中“1”的數(shù)量,，這可以在“部分積產(chǎn)生電路”中降低部分積的數(shù)量，“部分積產(chǎn)生電路”產(chǎn)生的部分積在“改進(jìn)后的陣列加法器”和“超前進(jìn)位加法器”中相加,，最后得到乘積z,。

2 降低部分積數(shù)量的編碼算法
    設(shè)x,，y是被乘數(shù)和乘數(shù)，它們分別用24位二進(jìn)制數(shù)表示,，最高位是符號位,，z是乘積，用47位二進(jìn)制表示,，最高位是符號位,，“1”表示負(fù)數(shù)，“0”表示正數(shù),。則它們的關(guān)系可以用下式表示：
                     
   
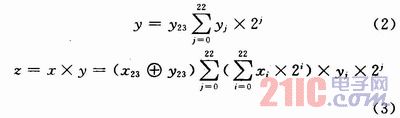
    式中：xi,，yi分別是x，y的權(quán)位,。如果按式(3)進(jìn)行乘法計(jì)算,，需要將與所有的yi相乘，產(chǎn)生23行部分積,，然后再將其相加,，即使yi=0，也要進(jìn)行上述運(yùn)算,，這樣就勢必增加乘法器的功耗和延時(shí),，因此，在下面將會對全加器和半加器進(jìn)行改進(jìn),，使僅與yi=1相乘,，從而避免與yi=0相乘。首先介紹降低乘數(shù)y中“1”的數(shù)量的編碼算法,。用一個(gè)事例說明本文介紹的算法的優(yōu)越性,。設(shè)m1，m2分別是乘數(shù)和被乘數(shù),，且令m1=01110111,，如果用m2與m1中的每一位相乘，則會產(chǎn)生6個(gè)m2和2個(gè)“0”列,，如果按照Sanjiv Kumar Mangal和 R． M．   Patrikar所建議的方法,，則：
    01110111(m1)=10001000(n1)-00010001(n2)    (4)
    將m2分別與n1和n2相乘，再將它們的乘積相減即得乘積結(jié)果,。但是,，在這一過程中，一共產(chǎn)生4個(gè)m2,。如果按照本文所建議的方法，會進(jìn)一步降低m2的數(shù)量,，即：
    01110111(m1)=10000000(n1)-00001001(n2)    (5)
    由式(5)可以看出,，n1和n2中共有3個(gè)“1”，因此，可以進(jìn)一步降低部分積的數(shù)量,。當(dāng)乘數(shù)的位數(shù)較大時(shí),，本文提出的算法優(yōu)越性更大。具體編碼流程如圖2所示,。

3 部分積的產(chǎn)生及相加
    在數(shù)字電路中,，功耗主要由3部分構(gòu)成，即：
   
    式中：Pdynamic是動(dòng)態(tài)功耗,；Pshort是短路功耗,；Pleakage是漏電流功耗。當(dāng)CMOs的輸入信號發(fā)生翻轉(zhuǎn)時(shí),，會形成一條從電源到地的電流Id對負(fù)載電容進(jìn)行充電,，從而產(chǎn)生Pdynamic。一般情況下,，Pdynamic占系統(tǒng)功耗的70 ％～90％,。因此，有效地降低Pdynamic也就降低了電路功耗,。
    為了降低CMOS輸入信號的翻轉(zhuǎn)活動(dòng)率,，本文對部分積相加過程中用到的全加器和半加器進(jìn)行了必要的改進(jìn)，從而避免當(dāng)乘數(shù)y的某一位是“0”時(shí)輸入信號的翻轉(zhuǎn),，本文的全加器和半加器的結(jié)構(gòu)如圖3所示,。

    圖3中，xi+1,，xi分別是被乘數(shù)的某一位,，yi是乘數(shù)的某一位，ci,，ci+1,，co是加法器的進(jìn)位輸出信號，si是加法器的和,。
    從圖1中可以看到,，y經(jīng)過編碼以后得到兩個(gè)數(shù)b和c，其中,，b是24位二進(jìn)制數(shù),，c是21位二進(jìn)制數(shù)。由式(5)可得到下式：
    z=x×b-x×c (7)
    為了降低乘法器的延遲,，將b和c分別分成三部分(即 b[23：16],，b[15：8]，b[7：0],，c[20：16],，c[15：8]和c[7：O]),，x分別與這6個(gè)數(shù)相乘可以得到6組部分積，每一組部分積分別采用圖4所示的陣列加法器相加,，即得到6個(gè)部分積和(sb2,，sb1，sb0,，sc2,，sc1，sc0),。圖4中的HA,，F(xiàn)A0，F(xiàn)A1分別對應(yīng)圖3中的HA,，F(xiàn)A0,，F(xiàn)A1；ADD是FA0改進(jìn)前的全加器,。則sb2,，sb1和sb0錯(cuò)位相加可以得到x×b的積sb，sc2,，sc1和sc0錯(cuò)位相加可以得到x×c的積sc,，所有這些錯(cuò)位相加以及得到最后的乘積z都是通過超前進(jìn)位加法器來實(shí)現(xiàn)的。

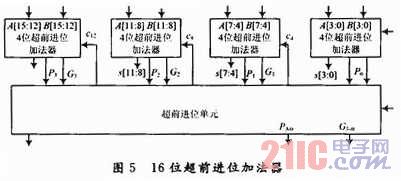
    在由sb,，sc得到z的兩個(gè)47位二進(jìn)制數(shù)相加過程中,，用到了3個(gè)如圖5所示的16位二進(jìn)制加法器，它包括4個(gè)4位超前進(jìn)位加法器和1個(gè)超前進(jìn)位單元(其中,，Pi為進(jìn)位傳播函數(shù),，Gi為進(jìn)位產(chǎn)生函數(shù))。錯(cuò)位相加過程中用到的超前進(jìn)位加法器與圖5中16位超前進(jìn)位加法器結(jié)構(gòu)類似,，在此不再闡述,。

4 仿真與功耗測試結(jié)果
    圖6所示是乘法器的功能仿真波形圖，可以看到,，本文所介紹的乘法器的功能是正確的,。

    本文所介紹的乘法器是由VerilogHDL編程實(shí)現(xiàn)的，因此,，在Altera的FPGA芯片EP2C70F896C中進(jìn)行功耗測試,，功耗測試過程中環(huán)境變量設(shè)置如表1所示。

    對功耗的測試時(shí)間是1μS,。在測試時(shí)間內(nèi),，給乘法器加入不同的測試激勵(lì)，觀察功耗變化情況,，為了說明本文提出的算法的優(yōu)越性,，同時(shí)也測試了由現(xiàn)有的兩種編碼算法所實(shí)現(xiàn)的乘法器,，測試結(jié)果分別如表2～表4所示(其中，whole表示表格前部的測試激勵(lì)在測試時(shí)間內(nèi)依次輸入),。

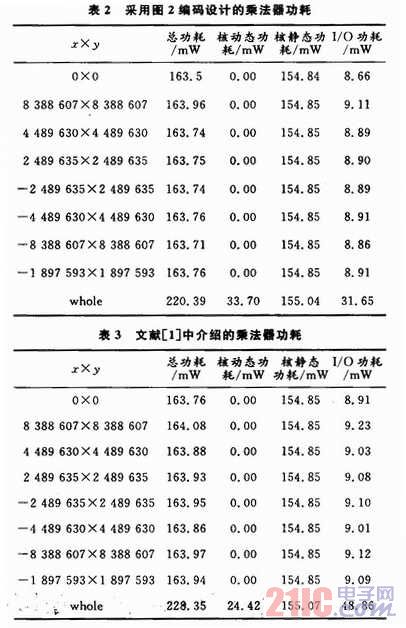
    從圖6中可以看出，在測試時(shí)間內(nèi),，當(dāng)測試激勵(lì)保持不變時(shí),，F(xiàn)PGA芯片的核動(dòng)態(tài)功耗0．00 mW，總功耗比較小,，用三種編碼算法實(shí)現(xiàn)的乘法器功耗差別不大,，說明在只進(jìn)行一次乘法運(yùn)算時(shí)，COMS的輸入信號基本沒有翻轉(zhuǎn),；當(dāng)輸入激勵(lì)在測試時(shí)間內(nèi)變化,，即在whole狀態(tài)時(shí)，三個(gè)乘法器都有動(dòng)態(tài)功耗,，說明CMOS的輸入信號隨著電路輸入信號的變化而翻轉(zhuǎn),。本文介紹的乘法器的總功耗比文獻(xiàn)介紹的算法降低了3．5％，比基于Booth-Wallace Tree的乘法器的功耗降低了8．4％,。

5 結(jié)語
    本文介紹了一種新的編碼方法,，它相對于文獻(xiàn)中的編碼可以進(jìn)一步降低乘數(shù)中“1”的數(shù)量，從而進(jìn)一步降低了乘法器的功耗,；另外,，還對傳統(tǒng)的全加器和半加器進(jìn)行了改進(jìn)，從而降低CMOS輸入信號的翻轉(zhuǎn)率,，從而降低了功耗,。并且，通過在Altera公司的FPGA芯片EP2C70F896C中進(jìn)行功耗測試,，可以看出本文介紹的乘法器的功耗比文獻(xiàn)中介紹的乘法器的功耗降低了3．5％,，比基于Booth-Wallace Tree的乘法器的功耗降低了8．4％。