本文針對65×65mm一面設(shè)有九顆1×1mm,、1W的LED芯片,，另一面為肋片的鋁制散熱" title="散熱">散熱片，利用數(shù)值法求解三維穩(wěn)態(tài)導(dǎo)熱微分方程,，利用計算機(jī)專用軟件計算得到不同LED芯片分布時,，散熱片芯片表面的溫度分布，根據(jù)其溫度場來分析LED芯片分布對其散熱的影響,。結(jié)果是：九顆芯片集中在一起散熱效果最差,，芯片之間的距離應(yīng)達(dá)到5mm以上，其芯片溫度可降低近5℃以上,。

      引言

　　LED照明,，由于節(jié)能顯著，被認(rèn)為是下一代照明技術(shù),。LED是冷光源,，其光譜中不包含紅外部分，而目前LED發(fā)光效率" title="發(fā)光效率">發(fā)光效率僅達(dá)到20%,，也就是說有80%以上的電能轉(zhuǎn)換成熱能,。如果熱量不能有效散出,，芯片的溫度上升，會導(dǎo)致光效下降,，光衰加劇,，嚴(yán)重時燒毀芯片，LED芯片散熱是當(dāng)前LED照明發(fā)展中的一大未解決的問題,。LED芯片的散熱過程并不復(fù)雜,，只是一系列導(dǎo)熱過程再加對流換熱過程，溫度范圍不高,，屬于常溫傳熱,，其內(nèi)的導(dǎo)熱過程，完全可以運(yùn)用計算機(jī)專用軟件求解三維導(dǎo)熱微分方程,，計算分析出LED芯片中,、散熱片內(nèi)的導(dǎo)熱過程，以及散熱片外表的對流換熱,，分析出整個傳熱過程中主要的熱阻在何處,，什么原因造成的，可以得到一非常清晰的解,，使人們有的放矢,。但當(dāng)前LED散熱以及同類的半導(dǎo)體芯片散熱，都缺少這一基礎(chǔ)性和指導(dǎo)性的研究,，即使有人做了,，但不為眾人所知。由此造成當(dāng)今LED散熱技術(shù)就像春秋戰(zhàn)國時代樣,，出現(xiàn)采用熱管,，甚至提出采用回路熱管。本文僅從LED芯片分布不同,，來研究分析其對散熱的影響,，將對LED芯片中的設(shè)計和制造起著指導(dǎo)性意義。

　　1,、計算模擬的模型

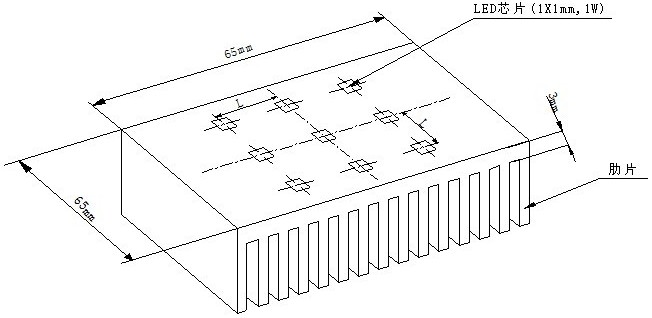
圖1

　　如圖1所示,，鋁制散熱片的一側(cè)面設(shè)有9顆1×1mm，1w的芯片,，還有0.1mm厚導(dǎo)熱系數(shù)取4w/(m·k)的絕緣導(dǎo)熱層,，肋片的總面積為 m2，空氣對流換熱系數(shù)為 =6 w/（m2·k）,，鋁的導(dǎo)熱系數(shù)取202 w/(m ·k),。為簡化計算，不考慮肋片內(nèi)的導(dǎo)熱問題，由肋片散熱面簡化折算成65×65mm,，對流換熱系數(shù)為 85 w/（m2·k）的對流換熱面,。也就是求解一側(cè)面為對流換熱面( =85w/（m2·k）)，另一側(cè)為9顆芯片(1×1mm,，1w)的鋁塊（65×65×3mm）在芯片間距不同時其內(nèi)部的溫度場,。

　　本文針對65×65mm一面設(shè)有九顆1×1mm、1W的LED芯片,，另一面為肋片的鋁制散熱片,，利用數(shù)值法求解三維穩(wěn)態(tài)導(dǎo)熱微分方程，利用計算機(jī)專用軟件計算得到不同LED芯片分布時,，散熱片芯片表面的溫度分布,，根據(jù)其溫度場來分析LED芯片分布對其散熱的影響。結(jié)果是：九顆芯片集中在一起散熱效果最差,，芯片之間的距離應(yīng)達(dá)到5mm以上,，其芯片溫度可降低近5℃以上。

      引言

　　LED照明,，由于節(jié)能顯著,，被認(rèn)為是下一代照明技術(shù)。LED是冷光源,，其光譜中不包含紅外部分,，而目前LED發(fā)光效率僅達(dá)到20%，也就是說有80%以上的電能轉(zhuǎn)換成熱能,。如果熱量不能有效散出,，芯片的溫度上升，會導(dǎo)致光效下降,，光衰加劇,，嚴(yán)重時燒毀芯片，LED芯片散熱是當(dāng)前LED照明發(fā)展中的一大未解決的問題,。LED芯片的散熱過程并不復(fù)雜，只是一系列導(dǎo)熱過程再加對流換熱過程,，溫度范圍不高,，屬于常溫傳熱，其內(nèi)的導(dǎo)熱過程,，完全可以運(yùn)用計算機(jī)專用軟件求解三維導(dǎo)熱微分方程,，計算分析出LED芯片中、散熱片內(nèi)的導(dǎo)熱過程,，以及散熱片外表的對流換熱,，分析出整個傳熱過程中主要的熱阻在何處，什么原因造成的，可以得到一非常清晰的解,，使人們有的放矢,。但當(dāng)前LED散熱以及同類的半導(dǎo)體芯片散熱，都缺少這一基礎(chǔ)性和指導(dǎo)性的研究,，即使有人做了,，但不為眾人所知。由此造成當(dāng)今LED散熱技術(shù)就像春秋戰(zhàn)國時代樣,，出現(xiàn)采用熱管,，甚至提出采用回路熱管。本文僅從LED芯片分布不同,，來研究分析其對散熱的影響,，將對LED芯片中的設(shè)計和制造起著指導(dǎo)性意義。

　　1,、計算模擬的模型

圖1

　　如圖1所示,，鋁制散熱片的一側(cè)面設(shè)有9顆1×1mm，1w的芯片,，還有0.1mm厚導(dǎo)熱系數(shù)取4w/(m·k)的絕緣導(dǎo)熱層,，肋片的總面積為 m2，空氣對流換熱系數(shù)為 =6 w/（m2·k）,，鋁的導(dǎo)熱系數(shù)取202 w/(m ·k),。為簡化計算，不考慮肋片內(nèi)的導(dǎo)熱問題,，由肋片散熱面簡化折算成65×65mm,，對流換熱系數(shù)為 85 w/（m2·k）的對流換熱面。也就是求解一側(cè)面為對流換熱面( =85w/（m2·k）),，另一側(cè)為9顆芯片(1×1mm,，1w)的鋁塊（65×65×3mm）在芯片間距不同時其內(nèi)部的溫度場。

      
      求解方程：

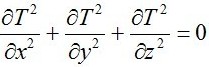
      即為三維穩(wěn)態(tài)導(dǎo)熱微分方程,，通常稱為拉普拉斯方程式,。利用專用的計算軟件求解。

　　2,、計算結(jié)果

　　圖2為：不同芯片間距,，LED芯片所處的散熱片金屬表面，過中心點(diǎn)的溫度分布,。

　　芯片間距L取1mm,、2.5mm、5mm,、7.5mm,、10mm、15mm、20mm,、25mm,、30mm。
     
　　當(dāng)L=1mm時,，即9顆LED芯片集中在一起,，之間沒間隙。
      
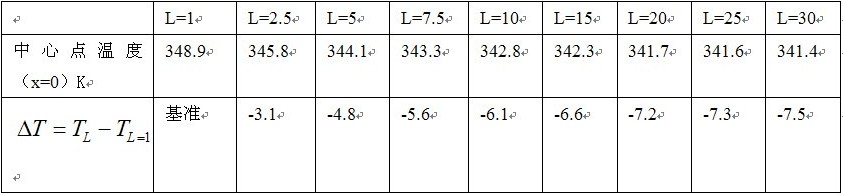
　　 表1列不同芯片間距,，LED芯片所處散熱片金屬表面中心點(diǎn)（也即溫度最高點(diǎn)）的溫度值及其差別,。以上計算中環(huán)境溫度取40℃（313K）。

(點(diǎn)擊圖片查看高清原圖)

　　3,、分析

　　從圖2和表1中可清楚地看：當(dāng)把9顆LED芯片集中在一起（芯片間距L=1mm）時,，中心點(diǎn)（芯片所處的溫度最高點(diǎn)）溫度最高，也就是散熱效果最差,。當(dāng)芯片間距增加1.5mm（L=2.5mm）時,，最高點(diǎn)溫度就下降3.1℃，芯片間距增加4mm（L=5mm）時,，最高點(diǎn)溫度下降4.8℃,。當(dāng)芯片間距為L=7.5mm時，最高點(diǎn)溫度下降5.6℃,。當(dāng)芯片間距L=10mm時,，溫度下降6.1℃。當(dāng)芯片間距L=20mm時,，溫度下降7.2℃,。在間距L=10mm內(nèi)溫度降低顯著。

　　4,、結(jié)果

　?。?）LED芯片分布對散熱有很大影響，應(yīng)該將LED芯片分散開,。

　?。?）對于1×1mm，1w的LED芯片,，芯片間距取5~10mm為佳,。

　　作者：秦 彪

　　參考文獻(xiàn)

　　[1] 楊世銘.傳熱學(xué).西安交通大學(xué),人民教育出版社，1980：36-163

　　[2] 俞左平.傳熱學(xué).山東工學(xué)院,人民教育出版社,，1979：1-169