目前的數(shù)字信號(hào)處理幾乎都是基于均勻采樣來描述信號(hào)特征,，但在許多實(shí)際的數(shù)據(jù)采集系統(tǒng)中,如激光陀螺捷聯(lián)慣導(dǎo)系統(tǒng)和多路A/D轉(zhuǎn)換電路中，由于采用整周期采樣技術(shù)或由于時(shí)鐘脈沖的不穩(wěn)定性,，造成采樣時(shí)間間隔是非均勻的,。在進(jìn)行譜分析和數(shù)字信號(hào)處理時(shí)，由于引入了時(shí)間歸一化過程,，采樣序列的自變量以整數(shù)形式給出,，沒有任何關(guān)于非均勻采樣時(shí)間間隔的信息，這必然導(dǎo)致頻譜分析及信號(hào)處理結(jié)果都存在誤差,。同時(shí)非均勻采樣在整個(gè)頻帶范圍內(nèi)都會(huì)產(chǎn)生頻譜噪聲,，甚至可以淹沒幅度小的信號(hào)頻譜，使得檢測(cè)和處理幅度小的信號(hào)較為困難,。
    國內(nèi)外學(xué)者對(duì)非均勻采樣信號(hào)的處理方法進(jìn)行了深入的研究,，JENQ Y. C.最早用分析的方法研究了非均勻理想抽取正弦信號(hào)的頻譜問題[1]，其基本思路是將非均勻采樣序列用M個(gè)均勻的采樣序列組合來表示,并建立非均勻采樣序列的離散頻譜和原來信號(hào)模擬頻譜之間的關(guān)系,。在此基礎(chǔ)上參考文獻(xiàn)[2]討論了非均勻采樣信號(hào)的頻譜分析方法,，從數(shù)學(xué)期望的角度證明了該方法的正確性。參考文獻(xiàn)[3-5]深入研究了非均勻采樣信號(hào)數(shù)字譜,，并給出了非均勻采樣周期信號(hào)的數(shù)字譜表達(dá)式,。在滑動(dòng)濾波方面，PELED A討論了滑動(dòng)濾波在信號(hào)處理中的應(yīng)用及其可行性[6],。雖然這些卓有成效的研究成果大大促進(jìn)了非均勻采樣信號(hào)分析理論的發(fā)展,，但只適用于多個(gè)周期采樣的疊加情況，同時(shí)對(duì)非均勻采樣信號(hào)的濾波問題還有待研究,。
     本文深入研究了非均勻采樣信號(hào)的數(shù)字譜,，得到了非均勻采樣信號(hào)數(shù)字譜計(jì)算的表達(dá)形式，提出了非均勻采樣信號(hào)的滑動(dòng)濾波方法,。應(yīng)用非均勻采樣信號(hào)的譜分析方法和滑動(dòng)濾波方法,，分析了激光陀螺輸出信號(hào)的譜特性，并有效地減少了激光陀螺的零偏信號(hào),。

式(2)得到的頻譜在頻域是連續(xù)的,，不適宜在計(jì)算機(jī)處理，為此需要對(duì)頻域離散化,。
     在時(shí)域上把非均勻采樣的N點(diǎn)按周期T0進(jìn)行周期延拓,即把該區(qū)間內(nèi)的波形平移nT0后疊加到原波形處形成周期波形,。由于周期延拓中的搬移可以通過與?啄(t-nT0)的卷積來實(shí)現(xiàn)，因此周期延拓后的波形在數(shù)學(xué)上可以表示為原始波形與沖激串序列的卷積,，其結(jié)果具有離散譜,。周期延拓信號(hào)為：
 
    這樣，經(jīng)過時(shí)域抽樣,、截?cái)嗪椭芷谘油睾?，在N個(gè)非均勻時(shí)間抽樣值與N個(gè)頻率抽樣值之間建立了聯(lián)系，而且經(jīng)過處理后的新信號(hào)的傅里葉變換Xs(k/T0)可以看成是原信號(hào)傅里葉變換的近似,。
2 非均勻采樣信號(hào)的滑動(dòng)濾波方法
    對(duì)于等間隔時(shí)間?駐T的采樣信號(hào)序列,滑動(dòng)平均濾波法就是連續(xù)取N次采樣值進(jìn)行算術(shù)平均,，其數(shù)學(xué)表達(dá)式是:

    非均勻采樣信號(hào)滑動(dòng)濾波器的頻譜計(jì)算如圖1所示。從圖1可以看到滑動(dòng)平均濾波相當(dāng)于一個(gè)低通濾波器,，衰減了較高頻率的信號(hào),，對(duì)數(shù)據(jù)起到了平滑作用。圖中實(shí)線為滑動(dòng)窗口寬度,，虛線為的振幅函數(shù)曲線,，窗口越寬通帶越窄。

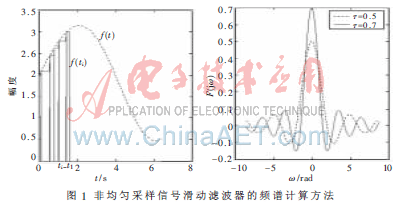
     利用這個(gè)特點(diǎn),，通過合理設(shè)置窗口寬度,，可以在抑制噪聲的同時(shí)盡可能保存信號(hào)，從而達(dá)到提高信噪比的目的,。從另一個(gè)角度來看,，滑動(dòng)窗口內(nèi)的數(shù)據(jù)在求平均時(shí)，由于噪聲是隨機(jī)的,，不會(huì)積累,，而信號(hào)會(huì)積累，所以信號(hào)得以突顯出來,。
3 仿真驗(yàn)證
     MATLAB作為數(shù)值分析和信號(hào)處理軟件,，已廣泛應(yīng)用于科學(xué)研究和工程實(shí)踐中解決各種實(shí)際問題,。本文利用MATLAB數(shù)據(jù)處理功能對(duì)非均勻采樣信號(hào)的數(shù)字譜進(jìn)行計(jì)算分析,，并且驗(yàn)證滑動(dòng)濾波方法的有效性。
 

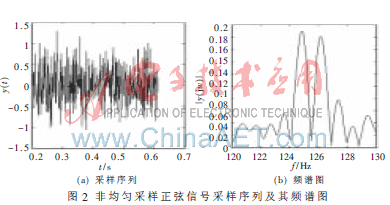
    因此,基于非均勻采樣的頻譜算法在處理相同數(shù)據(jù)長(zhǎng)度的采樣數(shù)據(jù)時(shí),，可以提高頻譜的頻率分辨率,。
    利用式(7)對(duì)混有噪聲的信號(hào)(式(9))進(jìn)行16點(diǎn)滑動(dòng)濾波處理，其誤差均值和方差為0.001 3,、 0.011 1,，而采用常規(guī)的平均濾波法對(duì)非均勻采樣信號(hào)進(jìn)行濾波處理，誤差均值和方差分別為0.002 8,、0.012 5,，從而驗(yàn)證了本文提出的滑動(dòng)濾波方法的有效性。
4 非均勻采樣信號(hào)滑動(dòng)濾波方法在工程實(shí)踐中的應(yīng)用
    激光陀螺是一種以量化脈沖的形式輸出角增量的數(shù)字傳感器,，它的讀出電路輸出脈沖個(gè)數(shù),，每個(gè)脈沖對(duì)應(yīng)著采樣時(shí)間內(nèi)的角增量,。而當(dāng)激光陀螺輸出量化脈沖的整數(shù)倍時(shí),測(cè)量信號(hào)的采樣間隔不是固定不變的，這就造成了采樣時(shí)間的非均勻性,，因此激光陀螺的輸出信號(hào)是非均勻時(shí)間采樣下的正弦信號(hào),。激光陀螺的零偏誤差是衡量其性能的主要技術(shù)指標(biāo)，它的大小直接關(guān)系到捷聯(lián)慣導(dǎo)系統(tǒng)的穩(wěn)定性和導(dǎo)航精度[7,，8],。
    圖3(a)為某型號(hào)激光陀螺整周期采樣的零漂信號(hào)，其均值和標(biāo)準(zhǔn)差分別為0.091 3 pulse/s和4.336 4 pulse/s,該零偏信號(hào)經(jīng)過常規(guī)的平均濾波和本文提出的非均勻滑動(dòng)濾波方法處理后,均值分別是0.107 5 pulse/s,、0.100 7 pulse/s,速率標(biāo)準(zhǔn)差分別是0.245 3 pulse/s,、0.220 4 pulse/s。從實(shí)驗(yàn)的結(jié)果可以看出,，經(jīng)過非均勻滑動(dòng)濾波器后激光陀螺零偏的標(biāo)準(zhǔn)差得到有效的減少,，誤差標(biāo)準(zhǔn)差較常規(guī)方法減少了10%。從經(jīng)過滑動(dòng)濾波處理后的數(shù)據(jù)可以準(zhǔn)確估算出激光陀螺的隨機(jī)游走系數(shù)為0.0064°/,。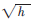

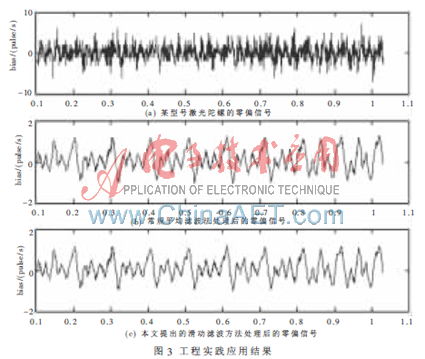
    針對(duì)數(shù)字信號(hào)處理中的非均勻采樣問題,，本文提出了非均勻采樣信號(hào)的頻譜分析和滑動(dòng)濾波方法。對(duì)非均勻采樣信號(hào)的數(shù)字譜進(jìn)行計(jì)算分析,，得出傳統(tǒng)的快速傅里葉變換要想提高頻率分辨率就要增加采樣點(diǎn)數(shù),，但這樣就增加了數(shù)據(jù)冗余性和計(jì)算的復(fù)雜性，而基于非均勻采樣的頻譜算法在處理相同數(shù)據(jù)長(zhǎng)度的采樣數(shù)據(jù)時(shí),，可以提高頻譜的頻率分辨率,。非均勻采樣滑動(dòng)濾波方法解決了采樣間隔不均勻的問題，衰減了高頻率的信號(hào),，對(duì) 數(shù)據(jù)起到了平滑的作用,。把這一研究成果應(yīng)用到機(jī)械抖動(dòng)激光陀螺正弦抖動(dòng)信號(hào)的分析和濾波處理中，激光陀螺的零偏誤差得到了有效的降低,。
參考文獻(xiàn)
[1]  JENQ Y C. Digital spectra of non-uniformly samples signals: Fundamentals and high-speed waveform digitizers[J]. IEEE Trans. Instrum. Meas.,1988,37(2):245-251.
[2] TARCZYNSKI A, VALIMAKI V,CAIN G D. FIR filtering of non-uniformly sampled signals [J]. IEEE Inter. Con. On Assp, 1997(3):2237-2240.
[3] OUAHABI A,DEPOLLIER C, SIMON L,et al. Spectrum estimation from randomly sampled velocity data[J]. IEEE Transactions on Instrument and Measurement, 1998,47(4):1005-1012.
[4]  JENQ Y C. Digital-to-Analog(D/A) converters with nonuniformly sampled signals[J]. IEEE Transactions on Instrumentation and Measurement, 1996,45(1):56-59.
[5] LIN Y P, VAIDYANATHAN P P. Periodically non-uniform sampling of band pass signals [J]. IEEE  Trans. Circuits and Systems. 1998(3):340-351.
[6] PELED A, LIU B. Digital signal processing,theory,design, and implementation. New York: John Wiley,1976:20-27.
[7]  高玉凱,鄧正隆.消除機(jī)械抖動(dòng)激光陀螺閉鎖誤差的方法[J].中國激光,，2007,34(3)：354-358.
[8]  高玉凱,鄧正隆.改善機(jī)抖溫度特性提高激光陀螺檢測(cè)精度的方法研究[J].系統(tǒng)仿真學(xué)報(bào),2007，19(14)：3297-
    3330.