文獻(xiàn)標(biāo)識碼： A
文章編號： 0258-7998(2010)12-0128-04
隨著通信網(wǎng)絡(luò)的迅猛發(fā)展,，實際應(yīng)用中人們對信息的依賴越來越強,，通信的內(nèi)容也不再局限于文字、符號等,，圖形,、圖像通信[1]日益深入到人們的日常生活中。由網(wǎng)絡(luò)通信的實時性和有效性所決定,，圖像要快速傳遞和存儲,，就必須進行壓縮。如何對圖像的數(shù)據(jù)信息進行壓縮,，使其在傳輸過程中盡量傳輸短的碼流，盡量節(jié)省信道容量,，進一步節(jié)約存儲空間,，這是圖像壓縮所要解決的問題,。圖像壓縮[2-3]就是去掉各種相關(guān)及冗余，保留重要的信息,。圖像數(shù)據(jù)本身所固有的視覺冗余及統(tǒng)計冗余等,為圖像壓縮提供了基本的理論支撐,。圖像壓縮的過程通常稱為編碼,而圖像的恢復(fù)則稱為解碼。因此,，圖像壓縮的關(guān)鍵就是尋找有效的編碼方法,，盡可能多地消除原圖像的信息冗余。
在突破傳統(tǒng)無損圖像壓縮[4]編碼方法的基礎(chǔ)上,，新興編碼方法在高效,、低碼等方面有極大的優(yōu)越性。而基于DCT(Discrete Cosine Transform)變換的JPEG(Joint Photographic Experts Group)[5-6]圖像壓縮標(biāo)準(zhǔn),，雖然在改善信噪比方面較以往有所提高,，但其運算復(fù)雜且不能避免方塊效應(yīng)的產(chǎn)生。分形[7]圖像壓縮編碼利用圖像整體與部分之間的自相似性,，在提高壓縮比方面有著很大的潛力,，但是如何正確地劃分子塊及尋找收斂的IFS(Iterated Function System)很困難。20世紀(jì)80年代在傅里葉變換[8]基礎(chǔ)上發(fā)展起來的小波變換,，有效實現(xiàn)了信號,、圖像的空頻轉(zhuǎn)換，圖像經(jīng)過小波分解后可以去除相關(guān)特性,，實現(xiàn)能量的重新分配,，使近似信息集中在低頻區(qū)域，細(xì)節(jié)信息反映在高頻區(qū)域,。根據(jù)小波系數(shù)的這一特點,，很容易實現(xiàn)圖像數(shù)據(jù)的壓縮。JPEG-2000圖像壓縮標(biāo)準(zhǔn),、MPEG-4視頻壓縮標(biāo)準(zhǔn)已經(jīng)將小波變換列入其中,。
圖像的小波變換就是以原始圖像為初始值，不斷將上一級圖像分解為4個子帶的過程,，每次得到的4個子帶圖像,，分別代表頻率平面上不同的區(qū)域，它們分別含有上一級圖像中的低頻和垂直,、水平及對角線方向的邊緣信息,。其中，子帶HLn表示了水平方向的高頻,、垂直方向的低頻成分,，子帶LHn表示了水平方向的低頻、垂直方向的高頻成分，而子帶HHn則表示了水平和垂直方向的高頻成分,。從多分辨率分析出發(fā),，一般每次只對上一級的低頻子圖像進行再分解。圖像小波變換示意如圖1所示,。
2 EZW算法
在圖像的小波系數(shù)矩陣中,，用“零樹”來描述這種依頻率特性遞減的數(shù)據(jù)分布特性。在“零樹”中,，通過區(qū)分零樹根(ZTR),、孤零(IZ)、正重要系數(shù)(POS)和負(fù)重要系數(shù)(NEG)這幾種不同性質(zhì)小波系數(shù)的方法,，來實現(xiàn)變換編碼的過程,，具體可參考文獻(xiàn)[9]。
嵌入式小波零樹編碼EZW(Embedded Zero tree Wavelet)算法[9],，就是利用零樹的一種高效的小波圖像壓縮算法,。實際中采用零樹與逐次逼近量化技術(shù)SAQ(Successive Approximation Quantization)相結(jié)合，構(gòu)成EZW編碼算法,。其主要步驟如下：
對圖像小波變換的研究表明,，一些較小的高頻系數(shù)幾乎應(yīng)該不再包含圖像信息，可以對這些信息進行噪聲抑制[12],，而不會對圖像的重構(gòu)質(zhì)量有大的影響,。所以當(dāng)逐次逼近的閾值落入這一相關(guān)區(qū)域時，可以停止對小波系數(shù)的掃描,。量化編碼前將這一部分系數(shù)作為噪聲進行濾波處理,，這也是對原算法可以進行改進的地方。
基于以上分析,，提出EZW的改進算法如下：
(1)圖像小波系數(shù)的重新排列,。為便于將圖像小波系數(shù)轉(zhuǎn)化到信號處理領(lǐng)域，并通過對信號的噪聲分離來求得原圖像中的噪聲冗余,，需要對代表原圖像的小波系數(shù)矩陣進行矢量排列,使其轉(zhuǎn)化為一個新的信號向量C,。具體方法是：首先對最低子頻帶LLn的小波系數(shù)矩陣按列排列成一個一個新的列向量c1,然后按照HLn，LHn,，HHn,，…，HL1,，LH1,，HH1的順序依次生成列向量c2，c3,，c4,，…,，c3n-1，c3n,，c3n+1,，最后令C=[c1;c2;c3;c4;c3n-1;c3n;c3n+1]，則生成信號向量C,。
(2)信號分解。將信號C進行小波分解,，進而將其分離為近似信息與噪聲細(xì)節(jié),。令C=S+U,其中S為近似信息，U為噪聲細(xì)節(jié),，則WTC=WTU+WTS,。WTC為小波變換算子;WTU對應(yīng)小波基中低通濾波部分，其還原的為近似信息;WTS對應(yīng)小波基中低通濾波部分,，其還原的為噪聲細(xì)節(jié),。此處的噪聲細(xì)節(jié)不能直接從信號C中直接去除，而是應(yīng)該利用其參數(shù)作為下一步閾值處理的依據(jù),。
(6)主掃描,。
(7)副掃描。
對于(6),、(7)中的掃描問題,，保持原算法(2)、(3)中的掃描及逐次逼近量化方式,。另外,，考慮圖像小波系數(shù)的零樹結(jié)構(gòu)特性，對每一次掃描中出現(xiàn)的零樹根節(jié)點,，與其對應(yīng)位置的更高頻帶的小波系數(shù)就不再參與掃描編碼,，這樣可以顯著地提高掃描編碼的效率。所以,，每次掃描的過程實質(zhì)上就是對重要系數(shù)的不斷量化細(xì)化的過程,。
(9)送熵編碼。
4 仿真實驗結(jié)果及分析
為驗證算法的有效性,，本文中采用的是256×256的lena圖像,，以Matlab 7.1為實驗仿真平臺。首先由函數(shù)命令imread讀入圖像信息,讀入后得一個大小為256×256的像素矩陣;用wavedec2函數(shù)對所讀取的二維圖像信息進行小波分解(這里取分解層數(shù)為N=3),，選取小波基為“db1”小波,。圖2為圖像小波分解后各層信息。對于本文設(shè)定的具體小波分解參數(shù),，可以得到由最低頻到各個方向高頻的共10個小波系數(shù)矩陣,，按照第3節(jié)中第(1)步所述的原則將其轉(zhuǎn)化為一新的信號向量C,。用離散信號的分解函數(shù)dwt對其進行信噪分離。圖3顯示的即為分解出的噪聲信息,。
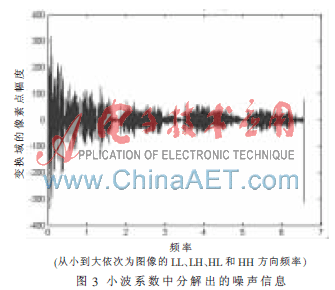
由噪聲樣本計算標(biāo)準(zhǔn)差,，得σ=14.28，按照式(4)可求得閾值δ=17.98,。對小波系數(shù)進行硬閾值化,，可以得到優(yōu)化以后的小波系數(shù)Cg，其中置零系數(shù)百分比perf0=86.36%,。為進一步確定Cg是否對原始圖像產(chǎn)生了失真,，可以通過小波逆變換重構(gòu)出圖像的灰度信息。圖4為原始圖像和閾值化處理后的重構(gòu)[14-15]圖像,。
由圖4可以看出,，兩幅圖像在視覺效果上已經(jīng)沒有區(qū)別，說明了閾值化處理的可行性,。
然后,，針對圖像小波域系數(shù)存在“零樹”結(jié)構(gòu)的特點，通過編寫逐次逼近量化的Matlab程序,，分別應(yīng)用原有算法和改進算法對lena圖像進行壓縮處理,。圖5為經(jīng)過相同的掃描次數(shù)，兩種算法圖像壓縮后所重構(gòu)的復(fù)原圖像,。
表1給出了對應(yīng)情況下的圖像質(zhì)量評價標(biāo)準(zhǔn)[16]：峰值信噪比(PSNR)和壓縮比(CR),。在仿真中，掃描終止時低頻閾值為TL=32,，高頻閾值為TH=16,。
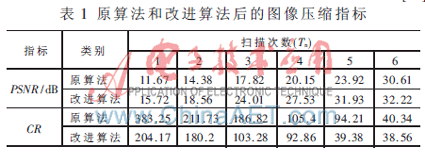
通過分析實驗結(jié)果可以得出，改進算法無論是在相同掃描次數(shù)下復(fù)原圖像的信噪比,，還是在相近信噪比下圖像的壓縮比(體現(xiàn)為相鄰斜對角參數(shù)的比較),，較之原算法都獲得了較大改善，這說明算法改進是成功的,。不足之處在于編碼過程中增加了小波系數(shù)的再處理,，對低頻和高頻分閾值量化，這對編,、解碼設(shè)備都提出了更高要求,。但從縮短碼流和節(jié)約信道資源方面，這些都是可以接受的,。
本文在分析和研究EZW圖像壓縮算法的基礎(chǔ)上,，提出了小波系數(shù)噪聲分離、閾值化小波系數(shù),、分閾值量化低頻和高頻信息的EZW改進算法,。實驗結(jié)果表明,，改進算法性能和壓縮比都有了提高，不失為一種行之有效的圖像壓縮算法,，同時它也為小波變換應(yīng)用于圖像壓縮編碼提供了一種新的思路,。
參考文獻(xiàn)
[1] DYCK W, SMODI R, HUFNAGL H, et al. High-speed JPEG coder implementation for a smart camera[J]. Journal of Real-time Image Processing,2006,1(1):63-68.
[2] 安曉東，陳靜.圖像壓縮方法綜述[J].電腦開發(fā)與應(yīng)用,，2006,，19（12）：24-26.
[3] BARANIUK R. A lecture on compressive sensing[J]. IEEE Signal Processing Magazine(S1053-5888), 2007,24(4):118-121.
[4] 蘇令華，呂韶昱,，萬建偉.基于多預(yù)測器的高光譜圖像無損壓縮[J].國防科技大學(xué)學(xué)報,，2007，29(1)：44-48.
[5] 趙楠楠,，孫紅星，徐心和.基于小波變換和SVM的圖像壓縮仿真研究[J].系統(tǒng)仿真學(xué)報,，2006,，18(11):3034-3037.
[6] ROBINSON J, KECMAN V. Combining support vector machine learning with the discrete cosine transform in image compression [J]. IEEE Transactions on Neural Networks (S1045-9227), 2003,14(4):950-958.
[7] 李明水，歐珊瑚,，張珩.分形圖像壓縮方法的新進展[J]. 工程圖學(xué)學(xué)報,，2004(2)：143-150.
[8] 陳長興，高曉光,，劉昌云.基于傅立葉變換的積分算法研究[J].系統(tǒng)仿真學(xué)報,，2004，16(4):817-819.
[9] 張春田,，蘇育挺,，張靜.數(shù)字圖像壓縮編碼[M].北京：清華大學(xué)出版社，2006.
[10] 張帆,，朱國仲.基于泛Fibonacci的Web圖像快速呈現(xiàn)[J].現(xiàn)代電子技術(shù),，2009（16）：103-106.
[11] CHENG A M K, SHANG Feng. Priority-driven coding and transmission of progressive JPEG images for realtime application[J]. Journal of VLSI Signal Processing System for Signal, Image and Video Technology(S0922-5773)，2006,79(12):1744-1753.
[12] 甘俊英,， 李春芝. 基于小波變換的二維獨立元在人臉識別中應(yīng)用[J]. 系統(tǒng)仿真學(xué)報,， 2007，19(3):612-616.
[13] 程正興.小波分析與應(yīng)用實例[M].西安：西安交通大學(xué)出版社,，2006.
[14] 石光明.壓縮感知理論及其研究進展[J]. 電子學(xué)報,，2009，37(5):1070-1081.
[15] TROPP J A, GILBERT A C. Signal recovery from randommeasurements via orthogonal matching pursuit [J]. IEEE Transactions on Information Theory (S0018-9448), 2007,53(12):4655-4666.
[16] 楊春玲,，高文瑞.基于結(jié)構(gòu)相似的小波域圖像質(zhì)量評價方法的研究[J].電子學(xué)報,，2009，37(4):845-849.