??? 摘? 要: 提出一種有效的計(jì)算級(jí)聯(lián)Z形碼最小距離的方法,。該方法將多維的級(jí)聯(lián)Z形碼并行地分成兩個(gè)低維數(shù)的分量碼,，其中有一個(gè)分量碼的維數(shù)固定為2,，然后找出所有能在該二維分量碼中產(chǎn)生低于某個(gè)已知的最小距離上限的輸入序列,，再驗(yàn)證這些序列在整個(gè)碼中產(chǎn)生的距離,，從而找出最小距離,。從最后數(shù)字結(jié)果來看,，使用普通的個(gè)人計(jì)算機(jī)，該方法能夠在111小時(shí)內(nèi)為碼率為1/2的級(jí)聯(lián)Z形碼找出最小距離20,，而在38小時(shí)內(nèi)為碼率為1/3的級(jí)聯(lián)Z形碼找到最小距離26,。?

??? 關(guān)鍵詞：? Z形碼； 最小距離,； 環(huán),； 聯(lián)合界

?

??? 近來隨著迭代譯碼技術(shù)的發(fā)展，許多具有非常優(yōu)秀性能的碼相繼被發(fā)現(xiàn)^[1-2],。其中級(jí)聯(lián)Z形碼(Concatenated Zigzag Codes)就是一種非常優(yōu)異而且編譯碼都簡(jiǎn)單的碼,，參考文獻(xiàn)[3]中給出的一個(gè)碼的性能離香農(nóng)限僅0.9dB。?

??? 通常計(jì)算一個(gè)碼的最小距離是一件非常困難的事,。參考文獻(xiàn)[3]中給出一種在一致交織器假設(shè)下計(jì)算級(jí)聯(lián)Z形碼的距離譜的算法,。但該算法不適用于確定性交織器場(chǎng)合。錯(cuò)誤脈沖法是非常有效的計(jì)算用迭代譯碼的碼的最小距離的方法,，如turbo碼^[4]、LDPC碼^[5],，但其缺點(diǎn)是不能保證計(jì)算結(jié)果的正確性,。在參考文獻(xiàn)[6]中，作者提出一種能夠計(jì)算turbo碼的真實(shí)最小距離的算法,，參考文獻(xiàn)[7]改進(jìn)該算法,，以增大計(jì)算的距離。本文提出一種利用環(huán)搜索來計(jì)算級(jí)聯(lián)Z形碼最小距離的有效方法,。?

1 級(jí)聯(lián)Z形碼?

1.1? Z形碼?

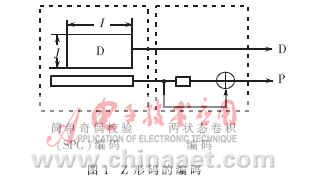
??? 圖1描述Z形碼的編碼過程,。首先信息序列被分成I段，每一段由J個(gè)比特組成,。然后每一段做奇偶校驗(yàn),，產(chǎn)生一個(gè)奇偶比特，這個(gè)過程就是簡(jiǎn)單奇偶校驗(yàn)碼(SPC)編碼過程,。然后這I個(gè)奇偶比特被送入一個(gè)只有兩個(gè)狀態(tài)的卷積編碼器,，進(jìn)行卷積運(yùn)算。使用d(i,j)i=1,2,…,I, j=1,2,…,J,來代表信息矩陣,，則奇偶序列p(i)i=1,2,…,I可以用如下的公式來產(chǎn)生：?

?????

?

?

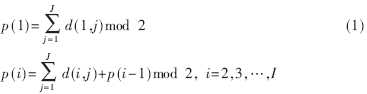1.2 級(jí)聯(lián)Z形碼?

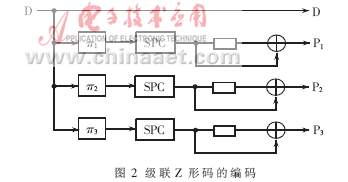
??? 一個(gè)K維的級(jí)聯(lián)Z形碼由并行的K個(gè)Z形碼和K個(gè)交織器組成,，見圖2。其稀疏奇偶校驗(yàn)矩陣可以用如下式來表示：?

?????

?

?

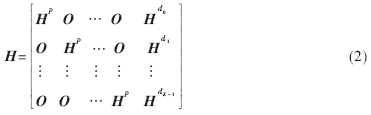??? 這里H^p是一個(gè)I×I的雙對(duì)角矩陣,，O是一個(gè)I×I的全零矩陣,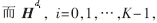，是一個(gè)I×IJ的稀疏矩陣, 該矩陣中“1” 的位置是由第i個(gè)交織器決定的,。?

2? 一個(gè)有效的計(jì)算最小距離算法?

??? 為了方便，將該算法分成當(dāng)級(jí)聯(lián)Z形碼維數(shù)為2維和大于2維的兩種情況,。?

2.1? 二維級(jí)聯(lián)Z形碼?

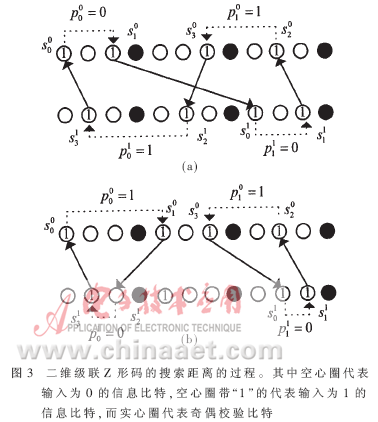
??? 對(duì)于一個(gè)二維的級(jí)聯(lián)Z形碼,，假設(shè)輸入重量為2w，根據(jù)Z形碼編碼原理,，如圖3所示,，按順序每?jī)蓚€(gè)“1”之間(用虛線表示)在每一個(gè)分量碼中所跨過奇偶重量之和就是該輸入序列產(chǎn)生奇偶校驗(yàn)總重量p。即:?

?????

??? 這時(shí)產(chǎn)生的碼字的總重量就是2w+p,。值得注意的是,，根據(jù)Z形碼的編碼規(guī)則，輸入重量為奇數(shù)的序列產(chǎn)生的奇偶校驗(yàn)序列,，相當(dāng)于在輸入序列最后插入一個(gè)“1”,，因而輸入重量為奇數(shù)的序列可以轉(zhuǎn)換為輸入重量為偶數(shù)的序列來考慮。另一方面,，當(dāng)級(jí)聯(lián)碼的維數(shù)只有2維時(shí),，圖中虛線和實(shí)線(代表交織關(guān)系)將沿著箭頭所指的方向形成一個(gè)閉環(huán)(圖3(a)），或多個(gè)閉環(huán)(圖3(b)）,。?

?

?

??? 一個(gè)簡(jiǎn)單的搜索單閉環(huán)的方法如圖3(a)所示,。首先在第一個(gè)Z形碼中選擇一個(gè)起始點(diǎn)s₀⁰，然后再在這個(gè)分量碼中選另一個(gè)點(diǎn)s₁⁰,，使得該點(diǎn)與s₀⁰之間的奇偶重量為一個(gè)確定的值p₀⁰,，顯然如果p₀⁰不為零，滿足這個(gè)條件的點(diǎn)s₁⁰有2J種,；而如果p₀⁰為零,，就只有J-1種。然后s₁⁰被唯一地交織到另一個(gè)分量碼上一個(gè)位置s₀¹,。然后再在這個(gè)分量碼中選一個(gè)點(diǎn)s₁¹,，使得該點(diǎn)與s₀¹之間的奇偶重量為p₀¹。接著s₁¹又被唯一地逆交織到第一個(gè)分量碼中的一個(gè)新位置s₂⁰,。這樣過程不斷進(jìn)行下去直到最后一個(gè)點(diǎn)s₃¹被確定,。如果最后s₃¹逆交織到第一個(gè)分量碼的點(diǎn)剛好是s₀⁰，則形成了一個(gè)閉環(huán),，該環(huán)中總的奇偶重量就為p,。對(duì)于多環(huán)，如圖3(b)所示,，可用同樣的方法得到每一個(gè)環(huán),，他們的總的奇偶重量就是p。?

??? 這樣計(jì)算最小距離的過程如下：?

??? 假設(shè)已知最小距離的一個(gè)上限為d^*。就要找出所有能夠滿足d^*≥2w+p的w和p,，而對(duì)于每一個(gè)p,，還要找出所有滿足(3)式的p_i^t，然后根據(jù)前面介紹的方法搜索單環(huán)和多環(huán),。?

??? 這樣就能找出所有能產(chǎn)生小于和等于d^*的輸入序列,，因而就能找出最小距離d_m。值得注意的是,，所有搜索到輸入序列產(chǎn)生的距離都是一個(gè)最小距離的上限,，因而都可以作為d^*，所以如果起初不知道d^*,，可以設(shè)一個(gè)很大的值,，比如N，然后再在搜索過程中利用搜索到輸入序列中產(chǎn)生的最小距離作為d^*,，使d^*不斷地逼進(jìn)d_m,。?

??? 下面分析尋找一個(gè)輸入重量為2w而奇偶重量為p的環(huán)所需要的計(jì)算量。?

2.2? 尋找一個(gè)環(huán)長(zhǎng)為p的單環(huán)的復(fù)雜度分析?

??? 我們知道,，給定一個(gè)值p,，能滿足(3)式的p_i^t的數(shù)目共有:?

?????

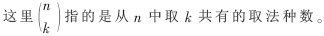??? 而對(duì)應(yīng)(3)式中，如果有λ(λ≤min(2w,p)個(gè)非零的p_i^t,，則在N_p中,，滿足這種情況的組合數(shù)為:?

?????

??? 而另一方面，對(duì)于每一個(gè)確定的p_i^t的分布,，如果p_i^t中非零的數(shù)有λ個(gè),，這種情況下，搜索一個(gè)環(huán)的復(fù)雜度為(2J)^λ(J-1)2^w-λ,。這樣當(dāng)給定w和p后,，對(duì)于每一個(gè)確定的起始點(diǎn),，搜索所有的單環(huán)復(fù)雜度為:?

?????

??? 從這個(gè)結(jié)果來看,，該算法能夠非常有效地降低計(jì)算最小距離的復(fù)雜度。?

2.3? K-維級(jí)聯(lián)Z形碼(K>2)?

??? 當(dāng)級(jí)聯(lián)Z形碼的維數(shù)K超過2時(shí),，將這K維碼分成兩個(gè)分量碼,，其維數(shù)分別為2維和K-2維。為了方便討論,，把2維的分量碼叫做基本分量碼,，而把K-2維的分量碼稱為導(dǎo)出分量碼。其方法是先在基本分量碼中找出所有能產(chǎn)生距離小于或等于d^*的輸入序列,，然后再檢查這些輸入序列在整個(gè)K維的級(jí)聯(lián)Z形碼產(chǎn)生的總距離,，這樣即可找到所有能產(chǎn)生小于和等于d_m的輸入序列。?

??? 注意，如果計(jì)算時(shí)間不受約束,，該算法一定能找出真實(shí)的最小距離和所有產(chǎn)生該最小距離的輸入序列,；而如果計(jì)算時(shí)間有限，則該算法只能找到最小距離的一個(gè)上限d^*,。?

3 數(shù)字結(jié)果?

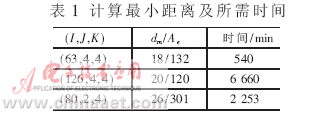
??? 下面對(duì)三個(gè)碼來計(jì)算其真實(shí)最小距離,。這三個(gè)碼的碼長(zhǎng)分別為504、1 008和480,，前兩個(gè)碼的碼率為1/2,，最后一個(gè)碼率為1/3。最終計(jì)算出的最小距離被列在表1中,。其中第一個(gè)碼的最小距離由輸入重量為4,、12、14三種序列產(chǎn)生,，第二個(gè)碼的最小距離由輸入重量16的序列產(chǎn)生,，而第三個(gè)碼最小距離由輸入重量為4的序列產(chǎn)生的。表1還給出了找出每一個(gè)碼最小距離所需要的時(shí)間,。所用的計(jì)算機(jī)為普通奔騰4個(gè)人計(jì)算機(jī),，主頻為2GHz。?

?

?

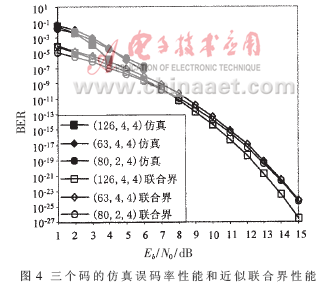
??? 圖4給出了這三個(gè)碼的BER性能仿真結(jié)果以及近似的聯(lián)合界結(jié)果,。該仿真采用的譯碼器為參考文獻(xiàn)[8]中給出的APP算法,，最大迭代次數(shù)為100。而近似聯(lián)合界計(jì)算由(8)式給出^[6]:?

?????

?

?

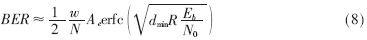??? 其中R為碼率,，E_b/N₀為每一個(gè)比特的信噪比,。從圖4中可看出，隨著信噪比的增加,，近似聯(lián)合界越來越接近仿真結(jié)果,，它們都能很好地反映一個(gè)碼在高信噪比時(shí)的誤碼率性能。?

??? 本文提出一種有效的計(jì)算級(jí)聯(lián)Z形碼最小距離的方法,。從其中的數(shù)字結(jié)果來看,，使用普通的個(gè)人計(jì)算機(jī)，該方法能夠在111小時(shí)內(nèi)為碼率為1/2的級(jí)聯(lián)Z形碼找出最小距離20,，而在38小時(shí)內(nèi)為碼率為1/3的級(jí)聯(lián)Z形碼找到最小距離26,。最后利用最小距離來計(jì)算近似聯(lián)合界，通過與誤碼率的仿真結(jié)果對(duì)比,，近似聯(lián)合界很好地反映了碼在高信噪比時(shí)的性能,，從而為評(píng)估碼的性能提供一種有效的手段。?

參考文獻(xiàn)?

[1] BERROU C, GLAVIEUX A, THITIMAJSHIMA P. Near shannon limit error-correcting coding and decoding:?turbo codes [C]// Proc IEEE Int Conf Communications.Geneve, Switzerland: IEEE Press. 1993: 1064-1070.?

[2] MACKAY D J C, NEAL R M. Near shannon limit?performance of low density parity check codes [J]. IEE lectron Lett, 1996,32(18):1645-1646.?

[3]?LI P, HUANG X L, PHAMDO N. Zigzag codes and?concatenated zigzag codes[J]. IEEE Trans Inform Theory,?2001,47(2):800-807.?

[4] BERROU C, VATON S, JEZEQUEL M, et al. Computing the minimum distance of linear codes by the error?impulse method[C]// Proc IEEE Global Telecommunications Conference. Taipei, Taiwan: IEEE Press, 2002:1017-1020.?

[5] HU X Y, FOSSORIER M P C, EELFTHEROU E. On?the computation of the minimum distance of low-density?parity-check codes [C]// Proc. 2004 IEEE Int Conf??Communications. Paris, France: IEEE Press, 2004:?767-771.?

[6] GARELLO R, PIERLEONI P, BENEDETTO S. Computing?the free distance of turbo codes and serially concatenated codes with Interleavers: algorithms and applications[J]. IEEE Journal on Selected Areas in Communications, 2001,19(5):800-812.?

[7] Ould-Cheikh-Mouhamedou Y,CROZIER S, KABAL P.Efficient distance measurement method for turbo codes?that use structured interleavers[J]. IEEE Commun. Lett,2006,10(6):477-479.?

[8] LI P. Modified turbo codes with low decoding complexity[J].IEE Electron. Lett., 1998,34(23):2228-2229.