在船舶通信中，船隊(duì)會(huì)組成鏈?zhǔn)疥?duì)列進(jìn)行航行,。船隊(duì)傳遞消息可以從一艘船接力傳遞給下一艘船,，每艘船需要準(zhǔn)確分離接收自己所需的消息，組成一種多目標(biāo)鏈?zhǔn)?a class="innerlink" href="http://forexkbc.com/tags/級(jí)聯(lián)" title="級(jí)聯(lián)" target="_blank">級(jí)聯(lián)網(wǎng)絡(luò),。每一艘船既是消息的接收方，又是傳遞消息的中繼方,。對(duì)于這種單一信源多個(gè)信宿所組成的鏈?zhǔn)郊?jí)聯(lián)通信網(wǎng)絡(luò)的容量,、可實(shí)現(xiàn)速率等問(wèn)題，學(xué)術(shù)界研究較少,。本文考慮該實(shí)際環(huán)境,，對(duì)其中的單源雙宿兩跳級(jí)聯(lián)網(wǎng)絡(luò)進(jìn)行研究。

        無(wú)線網(wǎng)絡(luò)信道容量的問(wèn)題最早源于參考文獻(xiàn)[1]提出的多用戶信息理論,，雖然沒(méi)有給出容量表述,，但定義了MAC信道；參考文獻(xiàn)[2]對(duì)MAC信道提出了一種簡(jiǎn)單的描述,； 參考文獻(xiàn)[3]首次提出廣播信道模型,； 參考文獻(xiàn)[4]針對(duì)三終端（或節(jié)點(diǎn)）模型定義并研究了中繼信道,；參考文獻(xiàn)[5]完善了該理論，雖然結(jié)論只針對(duì)單源單宿模型,，但對(duì)于整個(gè)網(wǎng)絡(luò)信息理論具有重要意義,。

        由于物理限制，實(shí)際網(wǎng)絡(luò)中無(wú)線節(jié)點(diǎn)無(wú)法在全雙工模式下進(jìn)行同時(shí)同頻收發(fā),，只能采取半雙工模式,。本文將對(duì)時(shí)分雙工模式下單源雙宿兩跳級(jí)聯(lián)網(wǎng)絡(luò)的容量區(qū)域進(jìn)行研究和分析。

1 系統(tǒng)模型

       考慮圖1的單源雙宿級(jí)聯(lián)無(wú)線網(wǎng)絡(luò),，定義信源S向目標(biāo)D₁和D₂分別傳輸消息x₁和x₂,，D₁接收x₁和x₂并解碼分離出x₁后作為中繼R并采用解碼轉(zhuǎn)發(fā)策略將消息x₂轉(zhuǎn)發(fā)給目標(biāo)D₂，信源S與節(jié)點(diǎn)D₂不考慮協(xié)作,。由于系統(tǒng)采用時(shí)分雙工,，節(jié)點(diǎn)不能同時(shí)接收與發(fā)送。若消息x₂不為空,，則完成一次網(wǎng)絡(luò)傳輸需要兩個(gè)時(shí)隙：

　　時(shí)隙1：源S將消息x₁和x₂發(fā)送給目標(biāo)D₁,；

　　時(shí)隙2：目標(biāo)D₁作為中繼R傳輸消息x₂給目標(biāo)D₂。

        假設(shè)完成一次完整的傳輸所用時(shí)間為1,，第一跳時(shí)隙長(zhǎng)度為t,，忽略保護(hù)間隔，則第二跳時(shí)隙長(zhǎng)度為1-t,。設(shè)每個(gè)節(jié)點(diǎn)都以滿功率發(fā)送消息,，第一跳容量為C₁，第二跳容量為C₂,。

2 單源雙宿兩跳級(jí)聯(lián)網(wǎng)絡(luò)容量研究

2.1網(wǎng)絡(luò)信息論基礎(chǔ)

        定理1 網(wǎng)絡(luò)流圖中源節(jié)點(diǎn)s發(fā)送信息到目的節(jié)點(diǎn)t,，其流量w的最大值等于所有s與t之間割集容量的最小值，即:

        參考文獻(xiàn)[6]采用構(gòu)造性證明該定理是可實(shí)現(xiàn)的,。該定理表明源節(jié)點(diǎn)與目的節(jié)點(diǎn)之間的最大流量等于其中最小的一個(gè)割集流量,，這就是最大流-最小割定理。

其中邊割集τ把網(wǎng)絡(luò)節(jié)點(diǎn)分割成不相交的兩個(gè)子集S和S^c,，S^c是S的補(bǔ)集,，如圖2所示。

        定理2的證明可參考文獻(xiàn)[4],，主要利用費(fèi)諾不等式和互信息的性質(zhì),。參考文獻(xiàn)[7]證明了多狀態(tài)網(wǎng)絡(luò)容量的割集上界。

        圖3為廣播信道的網(wǎng)絡(luò)流圖,，參考文獻(xiàn)[8]給出了廣播信道容量區(qū)的一個(gè)簡(jiǎn)單外界,。

        定理3 廣播信道的任意可達(dá)碼率(R₁,R₂)必存在某個(gè)分布q(x)，滿足:

        這個(gè)邊界表示的正是當(dāng)兩個(gè)譯碼器合作譯碼時(shí)可達(dá)的最大碼率,。對(duì)于廣播信道,，兩個(gè)接收機(jī)獨(dú)立工作,，所以它的可達(dá)碼率不會(huì)大于合作譯碼所能達(dá)到的碼率。

2.2 時(shí)分單源雙宿兩跳級(jí)聯(lián)網(wǎng)絡(luò)容量區(qū)域外界

        圖1所示的時(shí)分單源雙宿兩跳級(jí)聯(lián)網(wǎng)絡(luò)由于中間節(jié)點(diǎn)同時(shí)要擔(dān)負(fù)接收和中繼兩項(xiàng)工作,，常規(guī)級(jí)聯(lián)網(wǎng)絡(luò)模型并不適用于本網(wǎng)絡(luò),。根據(jù)在第一時(shí)隙，源節(jié)點(diǎn)需要將多個(gè)消息同時(shí)傳輸給中間節(jié)點(diǎn),，第一跳可以理解為源節(jié)點(diǎn)采用廣播信道的方式將多個(gè)消息發(fā)送給中間節(jié)點(diǎn),。該模型可以等價(jià)為圖4的形式。

        時(shí)隙1:源S利用廣播信道將消息x₁和x₂分別發(fā)送給目標(biāo)D₁和R,；

        時(shí)隙2:目標(biāo)R作為中繼節(jié)點(diǎn)傳輸信息給目標(biāo)D₂,。

        設(shè)D₁接收信號(hào)為y₁，D₂接收信號(hào)為y₂,；傳輸x₁和x₂的速率分別為R₁和R₂,，總速率R=R₁+R₂；信道容量分別為C₁和C₂,，其中C₁分為C₁₁和C₁₂兩部分,，C₁₁用于傳輸x₁，C₁₂用于傳輸x₂,。

　　由于采用時(shí)分,，割集須考慮鏈路激活時(shí)間。根據(jù)割集定理,，可將單源雙宿兩跳級(jí)聯(lián)網(wǎng)絡(luò)分割為：

        割集1：

證明：

        根據(jù)式(6)的約束區(qū)域,，雖然R₂的取值取決于其中的最小值，但為了避免通信資源的浪費(fèi),，兩跳鏈路上傳輸?shù)年P(guān)于消息x₂的信息量應(yīng)保持平衡,，即tC₁₂=(1-t)C₁₂，有:

該t值平衡了消息x₂的兩跳發(fā)送,，同時(shí)包含了兩個(gè)宿節(jié)點(diǎn)各自的信息量權(quán)衡,，因此它就是最優(yōu)時(shí)間分配系數(shù)：

        最后將t_opt代入上界約束條件式(6)中即可得出容量區(qū)域外界。

2.3 時(shí)分單源雙宿網(wǎng)絡(luò)的可實(shí)現(xiàn)速率

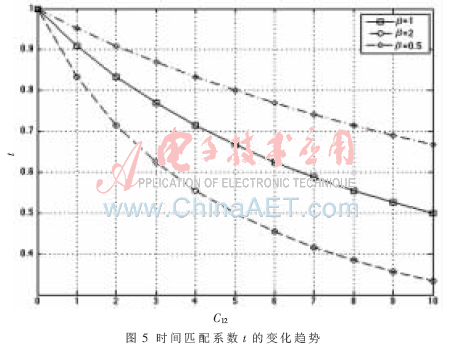
        根據(jù)信息論,，點(diǎn)對(duì)點(diǎn)傳輸信息的最大可實(shí)現(xiàn)速率等于信道容量,。參考文獻(xiàn)[7]指出了在多終端級(jí)聯(lián)網(wǎng)絡(luò)下可實(shí)現(xiàn)速率：

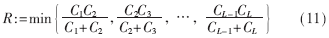
其中{C₁,C₂,…，C_L}是每一跳的可達(dá)速率,，也就是該信道的容量,。對(duì)于雙跳網(wǎng)絡(luò),，式(11)可簡(jiǎn)化為：

下面分別證明R₁,、R₂、R的可實(shí)現(xiàn)性：

        (1)只傳輸x₁

        假設(shè)S只傳輸x₁,，不傳輸x₂,，D₁只作為目標(biāo)存在,。C₁全部用來(lái)傳輸x₁，C₁₁=C₁,，C₁₂=0,。代入(7)可得R1的最大可實(shí)現(xiàn)速率為:

滿足點(diǎn)對(duì)點(diǎn)傳輸可達(dá)速率的最大值，因此R₁完全可以實(shí)現(xiàn),。

        (2)只傳輸x₂

        假設(shè)S只傳輸x₂,，不傳輸x₁，D₁只作為中繼R存在,。C₁全部用來(lái)傳輸x₂,，C₁₁=0，C₁₂=C₁,。則代入式(8)得到R₂的最大可實(shí)現(xiàn)速率：

符合參考文獻(xiàn)[8]提出的最大可實(shí)現(xiàn)速率,，R₂的可實(shí)現(xiàn)性得證。

        (3)同時(shí)傳輸x₁和x₂

        根據(jù)式(6)的制約關(guān)系,，R₁和R₂雖然無(wú)法達(dá)到單獨(dú)傳輸時(shí)所能達(dá)到的最大速率,，但根據(jù)式(7)、式(8)有：

        R₁和R₂都受C₁₂影響,。調(diào)整C₁₂可以使R₁和R₂同時(shí)滿足式(7),、式(8)給出的容量最值，又因?yàn)镽=R₁+R₂,，因此式(9)推導(dǎo)的總速率R可實(shí)現(xiàn),。

3 分析與討論

        將式(10)的時(shí)間分配系數(shù)t進(jìn)行等價(jià)變形為：

        根據(jù)式(15)，t的取值范圍和變化幅度會(huì)隨β變化,。這里分別取β={0.5,，1，2}三組數(shù)據(jù)進(jìn)行分析,。選取C₁=10,，C₂根據(jù)β的選取進(jìn)行調(diào)整,如圖5所示。圖中 t是C₁₂的單調(diào)遞減函數(shù),，減小速率取決于信道容量比β,。β越大，t衰減速度越快,，t可取值范圍越寬,；β越小，t衰減速率趨于平緩,，t可取值范圍相對(duì)變窄,。

　　容量曲線同樣受β的影響，以β=1為例，選取C₁=C₂=10,，如圖6所示,。可以看出：(1)R₁隨C₁₂增加,，衰減的速度最快,；(2)C₁₂取值最大時(shí)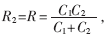，即傳輸消息的極限速率R₂就是總速率R的最小可達(dá)速率,，R的最小速率與β的取值成反比關(guān)系,。

　　綜合圖(5)和圖(6)有：增大β，消息x₁根據(jù)C₁₂的調(diào)節(jié)將占用更短的時(shí)隙,代價(jià)是犧牲了總體傳輸速率,；減小β,，可以提升R的最小傳輸速率，但會(huì)增大第一跳傳輸消息時(shí)所占用的時(shí)隙比例,。在實(shí)際中,，需要綜合其他因素進(jìn)行取舍，找到適合當(dāng)前環(huán)境下的參數(shù),。

        本篇論文依據(jù)最大流-最小割定理研究討論了時(shí)分雙工單源雙宿兩跳級(jí)聯(lián)網(wǎng)絡(luò)的容量問(wèn)題,。建立了求解處理無(wú)線網(wǎng)絡(luò)容量外界的有效方法，利用該方法找到了該模型的容量區(qū)域外界,，并對(duì)其可實(shí)現(xiàn)性進(jìn)行了證明,。最后進(jìn)行了分析驗(yàn)證，揭示了兩個(gè)信宿如何有效利用信道資源來(lái)完成各自消息的傳輸問(wèn)題,。

參考文獻(xiàn)

[1] SHANNON C E. Two-way communication channels[J]. In:Proc. 4th Berkelev Svm Math. Statist. and Prob. 1961,1(VD):611-644. 

[2] AHLSWEDE R. Multi-way communication channels[C]. in Proc. 2nd Int. Symp.Information Theory.Tsahkadsor,Armenian S.S.R., 1971:23-52. 

[3] COVER T M. Broadcast channels[J]. IEEE Trans. Inform.  Theory, 1972, IT-18, Jan: 2-14.

[4] COVER T M, THOMAS J A. Elements of information theory[J]. Wiley Series in Telecommunications, 1991.

[5] SENDONARIS A, ERKIP E, AAZHANG B. User cooperation diversity. Part I system description[J]. IEEE Trans.Commun,2003,51(11):1927-1938.

[6] 盧開(kāi)澄,盧華明.圖論及其應(yīng)用[M].北京:清華大學(xué)出版社,2005.

[7] KHOJASTEPOUR M A, SABHARWAL A, AAZHANG B.Bounds on achievable rates for general multi-terminal networks with practical constraints[C]. Information Processing in Sensor Networks (Lecture Notes in Computer Science). Berlin: Springer, 2003.

[8] SATO H. An outer bound to the capacity region of broadcast channels[J].IEEE Trans. Inform. Theory, 1978,24(3): 374-377.