??? 摘? 要：?采用雙Booth 2編碼技術(shù),，對高基radix-16 Montgomery模乘法器進行了優(yōu)化設(shè)計,，減小了電路面積，提高了模乘運算速度。使用SMIC0.18μm標準單元工藝庫綜合后,，計算256bit有限域GF(p)上的模乘只需要0.51μs。?

??? 關(guān)鍵詞： 布斯編碼,； Montgomery,； 有限域； 模乘法器

?

??? RSA算法,、數(shù)字簽名標準,、橢圓曲線密碼系統(tǒng)都要涉及到模乘或模冪運算。Montgomery模乘算法^[1]把模乘運算時的除法運算轉(zhuǎn)換成了簡單的移位操作,，大大提高了模乘運算的速度,，從而得到了廣泛的應(yīng)用^[2-4]。公鑰密碼體制中模乘運算的操作數(shù)位寬很大,，ECC需要160～512bit,，RSA等甚至達到1 024～2 048bit。直接利用原始的Montgomery模乘算法只能處理固定位寬的操作數(shù),，而且速度和面積均不理想,。為此,一種基于字的Montgomery模乘算法被提了出來^[2]，該算法不僅大大縮短了關(guān)鍵路徑,，而且可將操作數(shù)擴展到任意位寬,。目前已有多種基于這種算法的模乘法器設(shè)計方案^[3-4]。本文基于雙Booth 2編碼提出了另一種改進方案并進行了優(yōu)化設(shè)計,，使得模乘運算的速度得到了進一步的提高,。?

1 基于字的雙有限域Montgomery模乘算法?

??? Tenca^[2]提出了基于字的雙有限域Montgomery模乘算法?；谶@種算法設(shè)計的模乘法器采用基于字的操作數(shù)代替固定長度操作數(shù),，不但解決了大數(shù)加法進位鏈過長使電路關(guān)鍵路徑延遲太大的問題，而且使得模乘法器具有了可擴展性,，能支持任意位長的模乘,。把素數(shù)域GF(p)與二進制域GF(2^m)上的模乘統(tǒng)一起來則能在一個硬件上支持兩種域上的運算，從而節(jié)省了成本,?；谧值碾p有限域Montgomery模乘算法如下：?

??? Input: A,B,p,w,k,field?

??? Output: C∈[1,p-1]?

??? 1a: C=0?

??? 1b: spill=0?

??? 2: for i=0 to u-1?

??? 3: (spill|c0)=(a_ib₀)φc0?

??? 4: q=f(c₀,p₀,field)?

??? 5a: (spill|c0)=(q·p₀)φ(spill|c₀)?

??? 5b: for j=0 to e-1?

??? 5c: (spill|c_j)=(a_i·b_j)φc_jφspillφ(q·p_j)?

??? 6a: c_j-1=(c_j|c_j-1)/r mod w?

??? 6b: c_e-1=(spill|c_e-1)/r mod w?

??? 6c: c_e=0?

??? 7: if C>p, then C=C-p?

??? 算法把m bit模乘操作數(shù)擴展后看作基于字的向量，然后對操作數(shù)逐字掃描進行運算,。其中,p=(0,p_e-1,…,p₁,p₀),B=0(0,b_e-1,…,b₁,b₀),C=(0,c_e-1,…,c₁,c₀),A=(a_u-1,…,a₁,a₀),p_i,、b_i,、c_i是基為2^w的字，a_i是基為2^k的字,u=二進制域上多項式A(x)可以簡單地看成素數(shù)域上的A,，只是在部分積累加時有區(qū)別,，素數(shù)域上有進位的傳播，二進制域上為“異或”運算無進位,，算法中統(tǒng)一用φ表示,。函數(shù)f(c₀,p₀,field)只用到了c₀、p₀的最低k bit,，有限域GF(p)上q=(c₀·（2^k-p₀^-1))mod r,，有限域GF(2^m)上q=(c₀·p₀^-1)mod r。?

??? Tenca^[2]把上述Montgomery模乘算法組織成了流水線結(jié)構(gòu),。它包括s級處理單元（PE）,，每個PE運算單元做兩次一個字長的加法，加法器采用帶域選擇信號field的進位保留加法器（CSA）,，運算結(jié)果經(jīng)過一級流水線寄存器后傳給下一級PE運算單元,。PE經(jīng)重定時優(yōu)化后采用兩級寄存器結(jié)構(gòu)，第一級計算q,，第二級完成第5步的累加,。PE每次處理3bit的A，即對A的編碼采用基為8的Booth 3編碼,。為面向RSA應(yīng)用,，Yibo Fan^[3]在素數(shù)域GF(p)上對Tenca^[2]提出的結(jié)構(gòu)進行了優(yōu)化，采用基為16的Booth 4編碼,，提高了近26%的性能,。?

2 雙Booth 2雙有限域模乘法器的設(shè)計?

??? Yibo Fan^[3]采用的處理單元PE采用分裂基的方法簡化對a_i的Booth編碼，有效避免了不規(guī)則b_i,、p_i的倍數(shù)(如出現(xiàn)3b_i、7p_i),，但其需要六選一的數(shù)據(jù)選擇器,，而且左右兩個數(shù)據(jù)選擇器不一樣，造成布局布線的不規(guī)則,。本文經(jīng)研究發(fā)現(xiàn)可以把基為16的a_i分成兩個基為4的操作數(shù)同時操作,，仍然可采用類似分裂基的硬件結(jié)構(gòu)，而且左右數(shù)據(jù)選擇器相同,，使得VLSI實現(xiàn)時布線更容易,；對基為4的操作數(shù)采用Booth 2編碼后，編碼器結(jié)構(gòu)也更簡單,，數(shù)據(jù)選擇器的輸入只有0,、b_i,、-b_i、2b_i,、-2b_i,，它們只需要經(jīng)過簡單的移位與取反操作就能夠?qū)崿F(xiàn)，從而減小了電路面積,。編碼電路和數(shù)據(jù)選擇器電路更加簡單還可以縮短關(guān)鍵路徑的延遲,，從而提高了模乘法器的速度。?

2.1 總體結(jié)構(gòu)設(shè)計與優(yōu)化?

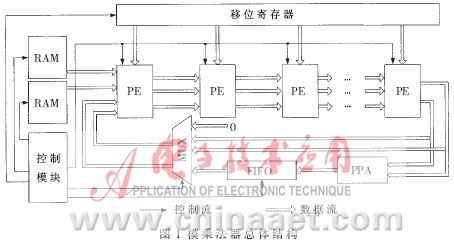
??? 雙Booth 2雙有限域模乘法器的核心仍然是基于字的Montgomery模乘算法,，因此也可以組織成流水線結(jié)構(gòu),，如圖1所示。它由s個處理單元（PE）,、一個移位寄存器,、兩個同步讀寫RAM、一個異步FIFO以及控制模塊組成,。移位寄存器根據(jù)算法外層循環(huán)依次移位輸出a_i,，兩個同步讀寫RAM則根據(jù)算法內(nèi)層循環(huán)輸出b_i、p_i,。如果在模乘運算中出現(xiàn)流水線溢出,，則把中間結(jié)果暫存到FIFO中，等待流水線空閑,；如果不出現(xiàn)流水線溢出,，則旁路掉FIFO直接使中間結(jié)果進入新的流水線。PE處理后的數(shù)據(jù)是以carry-save的冗余形式表示的,，中間數(shù)據(jù)位寬增大了一倍,，造成FIFO需要增大一倍。由于FIFO一路的中間結(jié)果不處在關(guān)鍵路徑上,，可以用一個并行前綴加法器PPA把carry-save冗余形式轉(zhuǎn)化為整數(shù)形式,，這樣可以節(jié)省一半的FIFO。Tenca^[2]實現(xiàn)的模乘法器中使用循環(huán)寄存器存儲b_i,、p_i需要占用大量的面積,而本文使用RAM代替可以充分利用標準單元庫的資源,，減小了電路面積。?

?

?

2.2 模乘處理單元結(jié)構(gòu)?

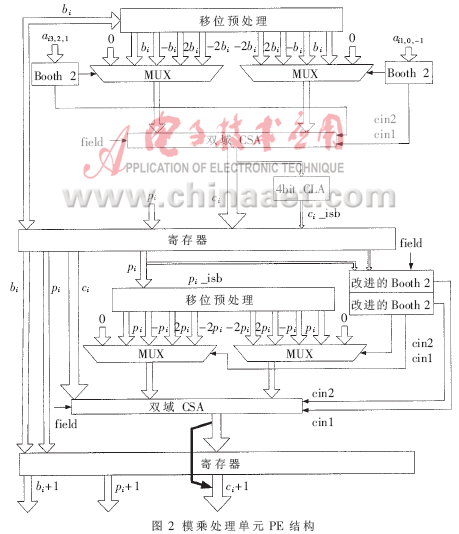
??? 模乘處理單元PE是模乘法器的核心部件,，若干級PE通過流水線寄存器串聯(lián)起來執(zhí)行大數(shù)模乘運算,，其電路結(jié)構(gòu)如圖2所示。它包含4個五選一的數(shù)據(jù)選擇器,、2個雙有限域進位加法器CSA,、1個4位超前進位加法器CLA、2個Booth 2編碼器,、2個修改的Booth 2編碼器及若干寄存器,。為了提高電路工作頻率,，用寄存器把PE電路分成兩個部分，使其用兩個時鐘完成部分積的累加,。為平衡路徑延遲,，把兩個CSA放在寄存器的兩邊。由于第二個時鐘周期內(nèi)的編碼電路比第一個時鐘周期內(nèi)的編碼電路要復雜,，延時更大,，如果把4位CLA放在第一個時鐘內(nèi)計算則剛好能達到大致平衡。?

?

?

??? 乘數(shù)A每次掃描4位,，分成兩組,，每組2位，經(jīng)Booth 2編碼后得到3位的輸入數(shù)據(jù)控制數(shù)據(jù)選擇器的輸出,。函數(shù)f通過編碼器實現(xiàn),，有限域GF(p)與GF(2^m)上的q值計算不一樣，因此需要同時編碼并通過域選擇信號field選擇輸出,。編碼輸出的四位q值再次經(jīng)過雙Booth 2編碼控制數(shù)據(jù)選擇器的輸出,。上述分兩步的編碼方式其中間值q是可以省略的，直接修改Booth 2編碼的輸入信號,，一次編碼完成,，部分編碼如表1所示。?

?

?

3 實現(xiàn)結(jié)果?

??? 基于雙Booth 2編碼的雙有限域模乘法器作為核心部件應(yīng)用在雙有限域ECC協(xié)處理器中,，根據(jù)協(xié)處理器的實際需要,，處理的最長操作數(shù)為384位，因此模乘法器采用4級流水,；b_i,、p_i的字寬為32位，便于與常用總線連接,。這種設(shè)計既考慮了處理速度,，又兼顧了電路占用的面積。模乘法器用Verilog語言描述,，采用Synopsys公司的Design Complier 在SIMC 0.18μm-typcal工藝庫下綜合,，等效“與非門”為4.5萬門，最高工作頻率可達280MHz,，完成一次GF(p)上的256bit模乘運算只需要0.51μs。表2是本文設(shè)計的模乘法器與已發(fā)表文獻中同類設(shè)計的比較結(jié)果,。表中結(jié)果顯示,本文設(shè)計的速度比最好的已發(fā)表的設(shè)計^[3]提高了16%,。?

?

?

??? 雙有限域模乘法器使用同一套硬件電路實現(xiàn)有限域GP(p)與GF(2^m)上的ECC模乘運算，節(jié)約了硬件成本,，擴展了運用空間,。本文基于雙Booth 2編碼對基為16的Booth 4編碼的模乘法器進行了優(yōu)化,，使得電路更加規(guī)范、簡單,。從實現(xiàn)結(jié)果可以看出,，本文的設(shè)計有效地減小了關(guān)鍵路徑延遲，提高了模乘法器的運算速度,。?

參考文獻?

[1] MONTGOMERY P L. Mondular multiplication without trial?division. Mathematics of Computation, 1985,44(7):519-521.?

[2] TENCA A F, SAVAS E, KOC C K. A design framework?for scalable and unified multipliers in GF(p) and GF(2m).?International Journal of Computer Research, 2004,13(1):68-83.?

[3] FAN Yi Bo, ZENG Xiao Yang, GANG Yi Yu,et al. A?modified high-radix scalable montgomery multiplier. IEEE??International Symposium on Circuit and System(ISCAS),?Island of ? Kos, Greece, May. 2006.?

[4] 史焱,吳行軍.高速雙有限域加密協(xié)處理器設(shè)計.微電子學與計算機,，2005,22(5):8-12.