量化誤差" title="量化誤差">量化誤差的產(chǎn)生
數(shù)字控制系統(tǒng)" title="控制系統(tǒng)">控制系統(tǒng)能夠為設(shè)計人員提供多種優(yōu)勢,如更易于實現(xiàn)高級算法功能、成本更低且性能更穩(wěn)定等。數(shù)字控制器" title="數(shù)字控制器">數(shù)字控制器避免了模擬控制中存在的漂移、噪聲敏感性以及組件老化等問題。設(shè)計數(shù)字馬達(dá)控制系統(tǒng)時需要考慮的主要問題是選擇合適的處理器,同時,處理器字長也至關(guān)重要。設(shè)計人員需要關(guān)注定點處理器中定點數(shù)表示法引起的量化誤差問題。這些誤差將會降低控制系統(tǒng)的性能,使設(shè)計人員無法最大限度地發(fā)揮出高級算法的優(yōu)勢。
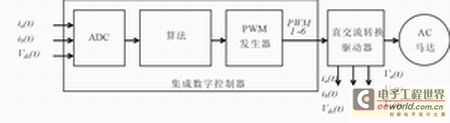
圖 1 通用數(shù)字馬達(dá)控制系統(tǒng)
圖 1 是通用數(shù)字馬達(dá)控制系統(tǒng)的結(jié)構(gòu)簡圖。算法可在數(shù)字控制器上實現(xiàn),數(shù)字控制器生成的控制輸出信號可通過逆變器驅(qū)動馬達(dá)。電流及電壓測量等反饋信號通過ADC反饋至該算法。
量化效應(yīng)產(chǎn)生誤差
數(shù)字信號與其表示的信號相近。現(xiàn)實世界中的信號在幅度和時間上是連續(xù)的,而數(shù)字信號的精度有限且在采樣時間上不連續(xù)。也就是說,在不考慮縮放比例的情況下,盡管數(shù)字信號與其真實的模擬量不同,但卻可以接受。圖1顯示了系統(tǒng)中不同的量化源 (quantization source)。比較明顯的量化源是:具有量化誤差、孔徑抖動、采樣與保持誤差特性的 ADC;具有截位、舍入、溢出誤差特性的計算引擎,具有時鐘驅(qū)動 PWM 生成功能的有限量化PWM發(fā)生器。
ADC 量化
對于所有采樣信號而言,控制系統(tǒng)信號的真實值與 ADC 代碼所代表的數(shù)值之間的差值即為系統(tǒng)的采樣誤差。主要是通過使用更長字長的 ADC 來最小化采樣誤差(在嵌入式控制器中通常采用 12 位ADC)。當(dāng)采樣孔徑正在進(jìn)行開關(guān)操作時,真實時間點的不確定性會造成孔徑抖動或不穩(wěn)定現(xiàn)象,必須通過將采樣時間點與 PWM 處理相結(jié)合的方法來控制這種現(xiàn)象,尤其是在具有最小抖動電流的采樣中。在 ADC 運行過程中,使用硬件觸發(fā)器可以消除由軟件運行引起的抖動。
特別要注意的是對多個電流測量值順序采樣時會產(chǎn)生誤差。通常情況下,設(shè)計人員希望及時得到馬達(dá)電流在某個特定時間點的瞬態(tài)圖,如果使用單個ADC對兩股電流進(jìn)行順序采樣,則會產(chǎn)生有限誤差。使用具有雙采樣和保持電路(可同時對雙通道進(jìn)行采樣)的ADC可以使此類誤差最小化,另一個誤差源是流入高速 ADC 輸入端的信號加載所引起的信號干擾。精心設(shè)計電路將有助于降低可能導(dǎo)致逆變器驅(qū)動級產(chǎn)生電壓干擾的電流峰值。
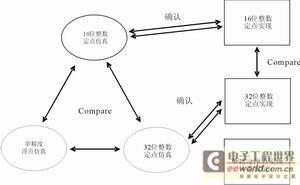
圖2 所選擇比較方法的概述
算法計算中的量化
算法的數(shù)值表示是量化效應(yīng)最關(guān)鍵的地方。算法表示的精度由字長決定。控制工程研究學(xué)深入研究了字長的選擇對控制系統(tǒng)性能的影響,然而,在將理論應(yīng)用于特定系統(tǒng)時會遇到兩個問題。實際上,對于三相 AC 感應(yīng)馬達(dá)中的磁場定向控制 (FOC) 等復(fù)雜馬達(dá)控制系統(tǒng)而言,量化效應(yīng)難以通過分析得出,原因是整個數(shù)字反饋系統(tǒng)是耦合、非線性、復(fù)雜和多輸入/多輸出的。其次,由于每個系統(tǒng)都具有獨特的設(shè)計,因此,單一的標(biāo)準(zhǔn)解決方案并不能完全適用于所有情況。分析因數(shù)值表示而引起的量化誤差的一個實用而高效的方法是:通過仿真及實驗分析來研究實際的數(shù)字控制器和控制方法。
三相 AC 感應(yīng)馬達(dá)的無傳感直接磁場定向控制系統(tǒng)顯示出了量化誤差的影響。圖2所示的系統(tǒng)已應(yīng)用于仿真與真實應(yīng)用中(需配備適當(dāng)?shù)耐庠O(shè)驅(qū)動器)。該算法采用 16 位、32 位定點及 32 位 IEEE-754 單精度" title="單精度">單精度浮點三種格式,這三種格式均采用基于 32 位定點數(shù)字信號處理技術(shù)的 TMS320F2812 數(shù)字信號控制器與 TI 針對 32 位定點編程的IQmath庫。IQmath 庫使設(shè)計人員能夠簡便快捷地將以浮點格式編寫的 C 語言代碼轉(zhuǎn)換為 32 位定點格式。代碼完全以 C 語言編寫,并具有IQMath庫提供的數(shù)學(xué)函數(shù)。
仿真系統(tǒng)能夠以 16 位、32 位定點及 IEEE754 單精度浮點三種格式表示,這里顯示的僅是其中一種選擇結(jié)果。由于定點處理器上的浮點運算是通過運行時間支持庫 (rts2800_ml.lib) 來實現(xiàn)的,本身效率不高,所以浮點版本的實現(xiàn)需要較長的采樣時間以便計算所有浮點模塊。由于不同的采樣時間將影響系統(tǒng)性能,為了便于比較,實驗結(jié)果將只側(cè)重于 16位~32位之間的定點版本。
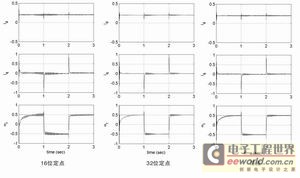
圖3 16 位定點、32 位定點及浮點仿真結(jié)果
要比較三種數(shù)據(jù)格式對數(shù)值精度的影響,需要監(jiān)控估算的速度響應(yīng)與相應(yīng)的 d 及 q 軸參考電流。將所有的 PI 增益、參數(shù)、基本量在全部三種數(shù)據(jù)格式的仿真過程中設(shè)定為相同的有效值。從圖3可以看出,16 位定點版本與浮點版本的性能具有極大的差別。
從圖3中數(shù)值性能的比較可以看出,16 位定點系統(tǒng)有若干個偽瞬態(tài) (false transient) 與振鈴,而 32 位系統(tǒng)則沒有這些現(xiàn)象。32 位單精度浮點與 32 位定點的結(jié)果非常相近。
在現(xiàn)實系統(tǒng)中,這些瞬態(tài)現(xiàn)象會產(chǎn)生可聽到的噪聲及振動,從而引起許多不良后果。尤其不利的是在第一個速度級別出現(xiàn)的估測速度振蕩瞬態(tài)的衰減以及隨后的增長,圖3中顯示,此次的觀察值十分接近 16 位系統(tǒng)的邊緣值。另一方面,具有控制響應(yīng)的 32 位定點仿真系統(tǒng)的性能良好。
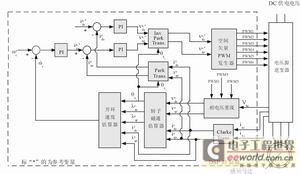
圖4 馬達(dá)控制系統(tǒng)的實現(xiàn)
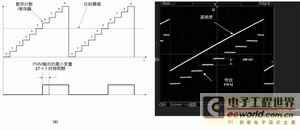
圖5 標(biāo)準(zhǔn) PWM 方案圖,以及高分辨率 PWM 與傳統(tǒng) PWM 的示波器圖比較
溢出現(xiàn)象一般會發(fā)生在通過控制算法進(jìn)行一系列的加、減法運算時。通過縮放算法來降低實際工作中的溢出可能性通常可達(dá)到調(diào)整溢出的目的。可使用額外的邊緣標(biāo)簽保護(hù)位 (margins labeled guard bit) 來完成。控制算法一般在標(biāo)么系統(tǒng) (per-unit system) 中進(jìn)行標(biāo)準(zhǔn)化,以便按比例縮放所有物理變量(電壓、電流、扭矩、速度及磁通量等)。使用合適的縮放比例可消除溢出這一量化誤差源。造成量化誤差的數(shù)值計算范例包括乘、除法運算以及三角、指數(shù)、平方根等查表數(shù)學(xué)函數(shù)。

