摘  要： 海雜波的建模方法已趨于成熟,，而如何在光柵顯示器上快速逼真地模擬海雜波是當(dāng)前模擬器面臨的一個(gè)重要問(wèn)題,。在成熟的海雜波模型基礎(chǔ)上，用ZMNL快速模擬雜波序列,，并通過(guò)距離和近程增益調(diào)制可快速逼真地模擬海雜波,。
關(guān)鍵詞： 海雜波；ZMNL,；距離調(diào)制,；近程增益調(diào)制

　迅速而準(zhǔn)確地模擬雷達(dá)雜波的方法對(duì)雷達(dá)系統(tǒng)模擬及雷達(dá)信號(hào)處理來(lái)說(shuō)十分重要[1]。目前海雜波建模主要有三種方式：散射機(jī)理建模,、雜波統(tǒng)計(jì)建模和雜波非線性建模,，其中雜波統(tǒng)計(jì)建模是最常用的方式[2]。產(chǎn)生具有一定概率分布的隨機(jī)序列的方法主要有：球不變隨機(jī)過(guò)程法(SIRP)和零記憶非線性變換法(ZMNL)[3],。海雜波在模擬中有著非常重要的地位,，如何將建模得到的海雜波快速逼真地反應(yīng)在模擬器的光柵顯示器上顯得尤為重要。本文采用經(jīng)典的海雜波模型,，通過(guò)ZMNL來(lái)產(chǎn)生海雜波序列,，再進(jìn)行距離和近程增益調(diào)制，可以快速逼真地模擬海雜波,。
1 常見的海雜波模型
　較為經(jīng)典的海雜波模型有：
　(1)瑞利分布[4]：

　
　(2)對(duì)數(shù)正態(tài)分布[5]：

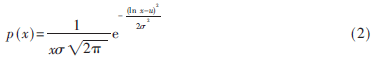
　式中,，x為海雜波幅度瞬時(shí)值，eu+σ/2為雜波幅度的均方值,。在分辨力提高或高海情下,，海雜波的后向散射特性偏離了瑞利分布，尾部較長(zhǎng),，適合于用對(duì)數(shù)正態(tài)分布模擬,。
　(3)韋布爾分布[6]：

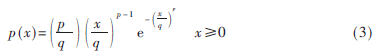
　式中,，p為比例參數(shù)，若p=2就成為瑞利分布,；若p=1就是指數(shù)概率密度函數(shù),。q為形狀參數(shù)，根據(jù)不同海情,，一般在1.4~2之間變化,。 海雜波幅度起伏較均勻，在高分辨力和低入射角的情況下Weibull分布更為合理,，雜波嚴(yán)重的情況下能更好地?cái)M合海雜波尾部拉長(zhǎng)的情況,。
　(4)K分布[7]：

　對(duì)高分辨雷達(dá)在低視角工作時(shí)獲得的雜波回波包絡(luò)模型的研究表明，用K分布不僅可以在很寬的范圍內(nèi)很好地與觀測(cè)雜波數(shù)據(jù)的幅度分布匹配,，而且還可以正確地模擬雜波回波脈沖間的相關(guān)特性,。
2 用ZMNL產(chǎn)生相應(yīng)的海雜波序列
　ZMNL法和SIRP法從兩種不同的途徑實(shí)現(xiàn)同時(shí)滿足一定幅度分布和一定相關(guān)條件的隨機(jī)數(shù)的產(chǎn)生，它們各有優(yōu)缺點(diǎn)[8],。ZMNL法優(yōu)點(diǎn)是計(jì)算量小,，易形成快速算法。但是需要進(jìn)行非線性變換,，而且該方法推導(dǎo)非線性變換前后相關(guān)之間的關(guān)系比較困難,。SIRP法的優(yōu)點(diǎn)是由于實(shí)現(xiàn)PDF相關(guān)特性可以獨(dú)立控制、容易推廣,，實(shí)現(xiàn)相干建模也比較容易,。SIRP甚至能由低階的PDF導(dǎo)出高階PDF，這一點(diǎn)對(duì)于精度建模尤其重要,。但其缺點(diǎn)也很明顯,，受所求序列的階數(shù)及自相關(guān)函數(shù)的限制，計(jì)算量大,、不易形成快速算法,。
　對(duì)于產(chǎn)生具有一定概率分布的隨機(jī)序列的方法，采用零記憶非線性變換法(ZMNL),，主要原因是此方法相比SIRP法其優(yōu)點(diǎn)是計(jì)算量小,、易形成快速算法。對(duì)于模擬器來(lái)說(shuō),，其實(shí)時(shí)性要求比較高,，要實(shí)時(shí)產(chǎn)生海雜波客觀上需要快速計(jì)算的方法。ZMNL主要方法是從獨(dú)立的高斯過(guò)程出發(fā),，得到相關(guān)高斯過(guò)程后經(jīng)過(guò)非線性變化再得到所需的非高斯過(guò)程,。其步驟如下[6]：
　(1)產(chǎn)生高斯白噪聲序列ni；
　(2)將高斯白噪聲序列ni通過(guò)一個(gè)線性濾波器H(Z),，得到高斯色噪聲序列xi,，即使xi各個(gè)時(shí)間點(diǎn)上的隨機(jī)變量具有某種相關(guān)性；
　(3)對(duì)相關(guān)高斯色噪聲序列xi進(jìn)行線性變換,，得到具有某種概率分布的相關(guān)序列zi,。以韋布爾分布為例，韋布爾分布隨機(jī)變量x可以用兩個(gè)正態(tài)分布的隨機(jī)變量w1和w2表示,，即：
　

3 海雜波的調(diào)制及模擬流程
　對(duì)于模擬的海雜波,，要能逼真地反應(yīng)在模擬器的光柵顯示器上，必須進(jìn)行距離衰減和近程增益控制的調(diào)制,。
　(1)海雜波的距離衰減
　任何雷達(dá)都有一定的作用距離,，雷達(dá)方程則是描述距離衰減的最簡(jiǎn)單有效的方式之一[9]。假設(shè)為理想無(wú)耗,、自由空間傳播時(shí)單基雷達(dá)方程：

　式中,，Pr為雷達(dá)接收的回波功率，Pt為雷達(dá)發(fā)射功率,，Gt,、Gr分別為發(fā)射天線和接收天線的增益，σ為目標(biāo)截面積,，λ為波長(zhǎng),，R為雷達(dá)到目標(biāo)的距離。雷達(dá)接收的回波功率與距離R的四次方成反比,，即與R-4成正比,，隨著R的增大，回波功率衰減得很快,。因此要逼真地模擬海雜波,，必須對(duì)模擬出的海雜波進(jìn)行距離上的衰減，由上式可知,，距離衰減模型可以選擇如上的指數(shù)模型,，即在模擬的雜波序列上按距離乘以一個(gè)指數(shù)衰減的因子。
　(2)海雜波的近程增益控制
　近程增益控制(STC)基本是每部雷達(dá)里都采用的處理措施,，也稱為“時(shí)間增益控制”或是“靈敏度時(shí)間控制”,。它主要用來(lái)防止近程雜波干擾使中頻放大器發(fā)生過(guò)載，對(duì)近區(qū)海域調(diào)低增益,，對(duì)遠(yuǎn)區(qū)海域則調(diào)高增益[10],。
　近程增益控制的基本原理是每次發(fā)射脈沖后，產(chǎn)生一個(gè)負(fù)極性隨時(shí)間漸趨于零的控制電壓,，供給被控的中放級(jí),，使接收機(jī)的增益按此規(guī)定電壓的形狀發(fā)生變化，如圖2所示,。它實(shí)際上是一個(gè)接收機(jī)靈敏度隨時(shí)間變化的調(diào)整電路,。由于海浪反射的功率與R呈指數(shù)的衰減形式,，因此接收機(jī)的靈敏度同樣按這個(gè)形式變化，如圖3所示,。

　由上述可知,，經(jīng)過(guò)靈敏度時(shí)間控制電路后，調(diào)節(jié)了不同距離的海雜波在P顯上的亮度,，因此STC的模擬也可以采用合適的指數(shù)模型,，即在模擬得到的雜波序列上按距離乘以一個(gè)指數(shù)型的STC控制因子。
　(3)海雜波的模擬流程
　對(duì)海雜波的模擬,，首先要產(chǎn)生一個(gè)相關(guān)的雜波序列,。根據(jù)ZMNL原理，以韋布爾分布序列為例,，當(dāng)選擇p=2.5,，q=2時(shí)可得到韋布爾雜波序列仿真結(jié)果如圖4所示。

　假設(shè)模擬器P顯距離上采用512個(gè)像素單元,，以某一方位為例,，闡述如下模擬逼真的海雜波回波：
　①模擬某一方位512個(gè)像素單元的韋布爾序列,，如圖5所示,。

　②對(duì)于該隨機(jī)序列,，要在P顯上反應(yīng)出海雜波特性,，應(yīng)將其幅度調(diào)制到光柵顯示器所用的色彩值范圍。一般采用RGB制式,，故應(yīng)將其幅度進(jìn)行亮度調(diào)制,，調(diào)制到0~255的范圍內(nèi)。此時(shí),，得到海雜波的亮度初始數(shù)據(jù)如圖6所示,。

　③由于雷達(dá)回波功率隨距離呈指數(shù)型衰減,，故將亮度調(diào)制得到的海雜波初始數(shù)據(jù)進(jìn)行距離衰減,，得到的距離調(diào)制后的亮度值如圖7所示。

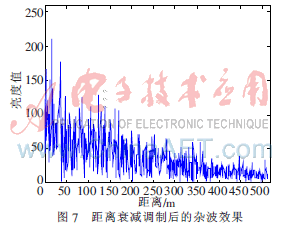
　與亮度變換后的海雜波圖比較,，距離衰減后的雜波整體上比雜波的初始數(shù)據(jù)要小,，且衰減規(guī)律呈指數(shù)型衰減，達(dá)到了距離衰減調(diào)制的效果,。
?、茉诶走_(dá)靈敏度時(shí)間控制電路調(diào)節(jié)下，海雜波在P顯上的亮度受到STC調(diào)制,，故將亮度調(diào)制得到的海雜波初始數(shù)據(jù)進(jìn)行STC調(diào)制,，得到STC調(diào)制后的亮度值如圖8所示,。

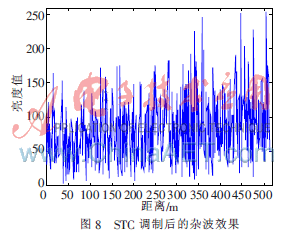
　與亮度變換后的海雜波圖比較，STC調(diào)制對(duì)近區(qū)的海雜波具有一定的抑制作用,，對(duì)遠(yuǎn)區(qū)的雜波則具有一定的增強(qiáng)作用,，調(diào)制按接收機(jī)的增益指數(shù)規(guī)律變化,。
?、菡鎸?shí)的回波是經(jīng)過(guò)距離衰減和STC調(diào)制后得到的，亮度調(diào)制得到的海雜波初始數(shù)據(jù)經(jīng)過(guò)距離和STC調(diào)制后,，即為模擬的海雜波,，如圖9所示。

　比較圖6,、圖7,，雜波在距離單元上有明顯的衰減；比較圖6,、圖8,，近區(qū)的雜波得到了進(jìn)一步的抑制，而遠(yuǎn)區(qū)的雜波,，則得到了一定程度的加強(qiáng),；在距離衰減和STC共同調(diào)制后模擬出了比較逼真的海雜波。
　對(duì)于服從韋布爾分布的雜波來(lái)說(shuō),，只需將比列參數(shù)p取2就可直接退化為瑞利分布,；如果p取1就可得到指數(shù)分布的雜波。對(duì)于不同海況的模擬,，可以調(diào)節(jié)形狀參數(shù)q,，在1.4~2之間變化，即可以通過(guò)調(diào)節(jié)形狀參數(shù)q的取值來(lái)模擬海況,。
參考文獻(xiàn)
[1] 高遠(yuǎn),，張揚(yáng)．海雜波的K-分布建模與仿真[J].電子科技， 2007,， 26(9)：52-55.
[2] 盧劍奇,，劉杰，嚴(yán)道明．雷達(dá)雜波建模與仿真方法研究[J]．微計(jì)算機(jī)信息,，2008,，24(10)：309-310．
[3] ISABELLE M． Study and simulation of sea clutter[J]． IEEE Signal Processing Workshop on Higher-Order Statistics， 1993,， 10(4)：178-181．
[4] MITCHELL R L．雷達(dá)系統(tǒng)模擬[M]．北京：科學(xué)出版社,，1982：33-45．
[5] 姜斌，和湘,，王宏強(qiáng),，等．改進(jìn)的Log-Normal分布雜波仿真方法[J]．電光與控制,，2006，37(1)：25-28．
[6] 宋新,，張長(zhǎng)隆,，周良柱．ZMNL方法實(shí)現(xiàn)海雜波建模與仿真[J]．現(xiàn)代雷達(dá)，2003,，27(3)：24-28．
[7] 趙海云,，胡學(xué)成．時(shí)空二維相關(guān)K分布雷達(dá)海雜波建模與仿真[J]．中國(guó)電子科學(xué)研究學(xué)報(bào)，2008,，3(5)：515-519．
[8] 蔡宗平,，劉山林．SIRP法學(xué)生t分布雷達(dá)雜波建模與仿真[J]．雷達(dá)科學(xué)與技術(shù)，2008,，6(3)：174-176.
[9] BARTON D K．雷達(dá)系統(tǒng)分析與建模[M]．南京電子技術(shù)研究所,，譯．北京：電子工業(yè)出版社，2007：120-123．
[10] 西北電訊工程學(xué)院《雷達(dá)系統(tǒng)》編寫組．雷達(dá)系統(tǒng)[M]．北京：國(guó)防工業(yè)出版社,，1980：453-461．