摘 要： 針對一般LDPC碼優(yōu)化方法無法有效實現(xiàn)IRA碼度分布優(yōu)化的問題,，提出了特定約束下IRA碼度分布的優(yōu)化方法。結(jié)合密度進(jìn)化的高斯近似算法優(yōu)化IRA碼度分布序列,，提取了IRA碼檢驗矩陣構(gòu)造的特定約束以改進(jìn)差分進(jìn)化算法,。仿真結(jié)果表明，所設(shè)計的度分布序列的噪聲門限高且搜索時間比改進(jìn)前減少30%,。
關(guān)鍵詞： 低密度奇偶校驗碼,； 度分布； 非規(guī)則重復(fù)累積碼,； 差分進(jìn)化
?
1962年,，Gallager在其論文中首先提出了LDPC碼(Low-Density Parity-Check Codes)[1]，但當(dāng)時并未受到重視,，直到上世紀(jì)末被Mackay重新發(fā)現(xiàn)后,，才掀起了一股研究與應(yīng)用的熱潮。LDPC碼是一類由非常稀疏的奇偶校驗矩陣及Tanner圖定義的線性分組前向糾錯碼,，它具有簡單的結(jié)構(gòu)描述與硬件復(fù)雜度,，可實現(xiàn)完全并行操作，有利于高速,、大吞吐能力譯碼,，譯碼復(fù)雜度亦比Turbo碼低，且具有更優(yōu)良的基底（Floor）殘余誤碼性能,，因此,，LDPC在現(xiàn)代通信系統(tǒng)中得到了越來越多的應(yīng)用。常用的非規(guī)則LDPC碼校驗矩陣的非系統(tǒng)比特部分為雙對角線結(jié)構(gòu),，即IRA碼(Irregular Repeat-Accumulate codes),，這種結(jié)構(gòu)的特點給度分布優(yōu)化設(shè)計增加了更多約束。本文研究的重點是分析IRA碼構(gòu)造方法,，從中提取碼構(gòu)造的特定約束,，并轉(zhuǎn)化為度分布序列中各分量的相關(guān)性描述，以便消除相關(guān)性,，利用差分進(jìn)化DE(Differential Evolution)搜索最優(yōu)化的度分布序列,，同時提出了改進(jìn)方法，在一定程度上加快了搜索速度和性能,。
1 IRA碼的構(gòu)造
1.1 度分布序列的定義
設(shè)LDPC碼的碼長為n,，信息比特長度為k，校驗比特長度為m,，則n=k+m,，碼率R=k/n,。λ(x):=Σλi xi-1代表非規(guī)則LDPC碼Tanner圖中變量節(jié)點(v-node)的度分布，ρ(x):=Σλi xi-1代表校驗節(jié)點(c-node)的度分布,。這里,，λi是度為i的變量節(jié)點連接的邊占Tanner圖中所有邊的比例，λi是度為i的校驗節(jié)點連接的邊占Tanner圖中所有邊的比例,，最大的變量節(jié)點度為dv,，最大的校驗節(jié)點度為dc。非規(guī)則LDPC碼度分布序列可表示為λ2λ3…λdv, ρ2 ρ3…ρdv),，容易驗證下列等式:
定義Nv(i)為度等于i的變量節(jié)點個數(shù),，Nc(i)為度等于i的校驗節(jié)點個數(shù)，推導(dǎo)得出:
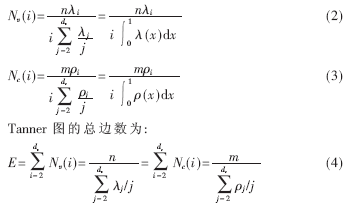
1.2 IRA碼構(gòu)造法
下面分析參數(shù)文獻(xiàn)[3]中IRA碼的構(gòu)造方法,。構(gòu)造一個(n-1,k)非規(guī)則LDPC碼,，其校驗矩陣為：
其中，H1是受度分布約束,、隨機(jī)產(chǎn)生的稀疏矩陣,，且不含重量為2的列；T包含了H中所有重量為2的列(即度為2的變量節(jié)點),。
在矩陣T最后添加度為1的列構(gòu)成H2,，產(chǎn)生一個新矩陣H，作為IRA碼的校驗矩陣,，如式(6),、(7)所示[3]:
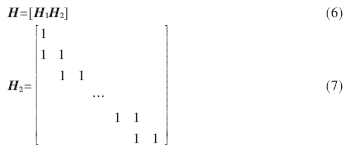
在校驗矩陣中添加度為1的列后，IRA碼度分布只有略微變化,，且該列位于校驗比特位置,，對BP(Belief-Propagation)迭代解碼后的誤碼率影響很小。從構(gòu)造方法可知,，IRA碼度分布受如下特殊約束：
約束：所有度為2的變量節(jié)點都分配給奇偶校驗比特,，且度為2的變量節(jié)點個數(shù)剛好為m(包括度為1的列)。m為IRA碼的校驗比特長度,。
通過推導(dǎo),，由(6)式得系統(tǒng)碼生成矩陣：
式中H2T為上三角矩陣，可用傳遞函數(shù)為1/1+D的差分編碼器實現(xiàn),，因此,，IRA碼很容易在硬件上實現(xiàn)快速編碼。
對于已知碼率為R的IRA碼設(shè)計,，設(shè)計約束實際上規(guī)定了度為2的變量節(jié)點個數(shù)和位置,，結(jié)合(4)式，有:
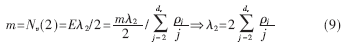
又根據(jù)(1)式，有:
從一個dv+dc-6維各分量不相關(guān)的分布矢量(λ4…λdv-1, ρ2…ρdc-1),，可依據(jù)(9)～(12)式依次計算ρdv,、λ2、λ3和λdv,從而唯一確定度分布序列,。
2 密度進(jìn)化的高斯近似和度分布優(yōu)化
??? 密度進(jìn)化理論是分析度分布序列噪聲門限值的強(qiáng)有力工具,，然而該理論涉及很多卷積運(yùn)算，運(yùn)算量大,。為了簡化計算,，Sac-Young Chung等針對加性高斯白噪聲信道AWGN(Additive White Gaussian Noise channel)提出了密度進(jìn)化的高斯近似分析方法。在消息獨立和消息密度高斯分布條件下,，該方法僅分析消息密度高斯分布均值，極大地減少了計算量,。這里列出高斯近似分析法的消息密度均值遞推公式:
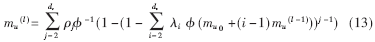
使用(13)式計算消息概率密度函數(shù),，從而得到迭代后解碼誤比特率，若誤比特率小于預(yù)設(shè)值ε(如10e-6),，則適當(dāng)增大σn2,，直到誤比特率大于ε。經(jīng)嘗試,，求得度分布(λ,ρ)在誤比特率小于ε時的最大σn2,，確定為該度分布的噪聲門限。
3 DE方法及改進(jìn)
DE是一種并行搜索方法,，能夠搜索連續(xù)空間非線性代價方程的全局極值,。該方法有能力使搜索跳出局部極值點，避免錯誤的收斂,。DE的特點在于產(chǎn)生測試參數(shù)矢量的方案,。以DE實現(xiàn)IRA碼度分布序列優(yōu)化的步驟如下，流程如圖 1所示,。
?
?
(1) 初始化：確定度分布序列中參與DE的變量個數(shù)L,，隨機(jī)產(chǎn)生Np個L維隨機(jī)矢量xi,g(0≤i≤Np-1，g為迭代次數(shù)),；
(2) 計算門限f(xi,g),，找出最大值，設(shè)門限最大的矢量為基本矢量xb,g(如圖中xb,g=xl,g),；
(3) 對于每一個矢量xi,g,，在其他矢量中隨機(jī)選擇兩個矢量xr1,g和xr2,g，定義F為權(quán)重因子,，以下式計算新矢量vi,g,，vi=xb,g+F(xr1,g-xr2,g);
(4) 新矢量ui,g的每個分量以概率CR取vi,g的對應(yīng)分量值，以概率(1-CR)取xi,g的對應(yīng)分量值；
(5) 選擇：如果 f(ui,g)> f(xi,g)則xi,g+1=ui,g否則xi,g+1= xi,g,；
(6) 停止準(zhǔn)則：如果超過了最大迭代次數(shù)或所有矢量已經(jīng)充分接近,，則迭代結(jié)束；否則跳轉(zhuǎn)到第(2)步,。
權(quán)重因子F對DE的影響很大,，增大F會加快收斂速度，但容易收斂于局部極值點,；減小F則效果相反,。這里，F(xiàn)取0.8,；測試矢量數(shù)Np取10L～30L,；交疊參數(shù)CR對DE的影響比F小，它更像一種微調(diào),，取較大的CR會加快收斂速度,，一般在[0.5,1]中取值。
使用DE搜索IRA碼的最優(yōu)度分布序列,，首先要消除度分布序列各分量的相關(guān)性,，否則搜索到的結(jié)果無法滿足IRA碼設(shè)計的特定要求。1.2節(jié)最后指出dv+dc-6維的分布矢量(λ4…λdv-1, ρ2…ρdv-1)中各分量消除了相關(guān)性,，并唯一確定度分布序列,，因此，筆者在優(yōu)化中使用該矢量,。
DE搜索IRA碼的最優(yōu)度分布序列相當(dāng)耗時,，特別是當(dāng)dv和dc較大，即測試矢量維數(shù)較大時,，差分進(jìn)化的速度很難讓人滿意,，根據(jù)一些先驗知識和測試結(jié)果，在不影響最終結(jié)果的前提下,，改進(jìn)了DE方法,，加快了優(yōu)化速度。
測試表明,，DE的大部分時間消耗于第二步的門限計算上,，因而，改進(jìn)的主要目標(biāo)是減少門限計算的時間,，為此首先要減少DE測試矢量維數(shù),。
先假定在IRA碼的度分布序列中只有(λ2λ3λ4λdv, ρdv-1 ρdv)大于零，其他都為零,，根據(jù)(9)～(12)式,，去相關(guān)性之后的矢量為(λ4,ρdv-1),，矢量維數(shù)從dv+dc-6維銳減為2維。實驗結(jié)果表明,，矢量每減少一維,，DE的收斂時間大約減少一半，改進(jìn)后DE可迅速收斂,。我們稱這種維數(shù)削減的DE過程為“DE_FIRST”,。一般來說，在dv不大時(如dv<10)結(jié)果已經(jīng)很接近最優(yōu)的度分布了,，但當(dāng)dv較大時結(jié)果距最優(yōu)的度分布仍有一定差距,，這時還要搜索更優(yōu)的度分布。適當(dāng)調(diào)整當(dāng)前的最優(yōu)矢量(λ2λ3λ4λdv, ρdv-1 ρdv),，在該矢量的一定范圍內(nèi)隨機(jī)產(chǎn)生L=dv-2個矢量,，并在此約束下隨機(jī)產(chǎn)生若干取值較小的矢量(λ5λ6…λdv,ρdv-2)組成dv-2維隨機(jī)矢量(λ4…λdv-1, ρdc-2， ρdc-1),，然后從DE的第二步開始繼續(xù)搜索,。這里并沒有擴(kuò)展(ρ2…ρdc-3)是因為將這些分量設(shè)為零幾乎不會影響優(yōu)化度分布的結(jié)果。擴(kuò)展后的隨機(jī)矢量唯一確定的度分布已經(jīng)十分接近最優(yōu)化的度分布了,，所以DE的收斂速度比一開始就隨機(jī)產(chǎn)生dv-2維隨機(jī)矢量的DE快很多。我們稱維數(shù)擴(kuò)展以后的差分進(jìn)化過程為“DE_SECOND”,。
通過分析大量優(yōu)化結(jié)果和其他文獻(xiàn)給出的優(yōu)化序列可以發(fā)現(xiàn),，λ4數(shù)值較小，大多取值在[0,0.2]內(nèi),，ρdc-1也比ρdc小,，一般取值在[0,0.4]。這樣,，“DE_FIRST”的初始隨機(jī)矢量選擇范圍可以減小,，在第一步中，矢量(λ4,ρdc-1)的兩個分量分別在上述兩個區(qū)間隨機(jī)產(chǎn)生,。實驗證明,，這樣做能夠加快搜索速度。
4 仿真結(jié)果
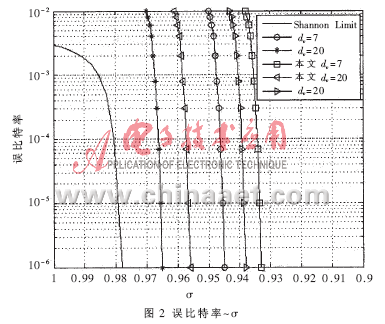
仿真參數(shù)設(shè)置如下：碼率為1/2,；差分進(jìn)化的Np=20L,，F(xiàn)=0.8，CR=0.8,。表1列出了用本文介紹的基于密度進(jìn)化高斯近似的DE搜索方法得到的最優(yōu)化度分布,，同時還列出了參考文獻(xiàn)[4]優(yōu)化得到的非規(guī)則LDPC碼度分布和參考文獻(xiàn)[5]同樣用密度進(jìn)化高斯近似優(yōu)化得到的非規(guī)則LDPC碼度分布。最后一行是度分布對應(yīng)的噪聲門限,。比較dv=20的噪聲門限可知,，本文方法得到的最優(yōu)化度分布優(yōu)于參考文獻(xiàn)[5]中的最優(yōu)化度分布，如圖2所示。由于優(yōu)化后的非規(guī)則LDPC碼的Nv(2)一般略大于(11)式規(guī)定的值,，因此在約束下搜索的IRA碼度分布中λ2比優(yōu)化的非規(guī)則LDPC碼度分布中λ2小,，如表1所示。若沒有IRA碼的設(shè)計約束,，本文介紹的方法可以搜索到更好的度分布序列,。表2是DE改進(jìn)前后收斂時間及噪聲門限?滓的對比(仿真程序運(yùn)行于1.5GHz PC機(jī))，可知,，改進(jìn)前后優(yōu)化的度分布噪聲門限很接近,，而改進(jìn)方法能夠節(jié)省大約30%的搜索時間。
?
本文通過分析IRA碼構(gòu)造方法的特定約束,，消除了度分布序列各分量之間的相關(guān)性,，從而利用DE方法搜索具有更高噪聲門限的度分布序列，并利用先驗知識改進(jìn)了DE方法,，加快了搜索速度,。這種方法也可以用來搜索其他構(gòu)造方式下優(yōu)化的度分布序列，對更廣泛的非規(guī)則LDPC碼優(yōu)化設(shè)計具有一定的借鑒意義,。
參考文獻(xiàn)
[1] ?GALLAGER R G. Low-density parity-check codes[J].IEEE Trans. Inform. Theory, August, 1962：21-28.
[2] ?JIN H, KHANDEKAR A, MCELIECE R. Irregular repeataccumulate codes[J]. in Proc. 2nd. Int. Symp. Turbo?Codes and Related Topics, Brest,France, Sept. 2000:1-8.
[3] ?YANG M, RYAN W E, LI Y. Design of efficiently?encodable moderate-length high-rate irregular LDPC
?codes[J]. IEEE Trans. Commun, 2004,52:564-571.
[4] ?RICHARDSON T, SHOKROLLAHI A, URBANKE R. Design of capacity-approaching irregular low-density paritycheck codes[J]. IEEE Trans. Inform.Theory, 2001,47(2):619-637.
[5] ?肖娟,王琳,鄧禮釗. 不規(guī)則LDPC碼的密度進(jìn)化方法及門限值確定[J]. 電子與信息學(xué)報, 2005,27(4):617-620.