摘 要: 提出了一個(gè)全新的混合算法并命名為微粒群差分算法,該算法在標(biāo)準(zhǔn)微粒群算法的基礎(chǔ)上結(jié)合了差分進(jìn)化算法用于求解約束的數(shù)值和工程優(yōu)化問(wèn)題。傳統(tǒng)的標(biāo)準(zhǔn)微粒群算法由于其種群?jiǎn)我恍匀菀紫萑刖植孔顑?yōu)值,針對(duì)這一缺點(diǎn)利用差分進(jìn)化算法中的變異、交叉、選擇3個(gè)算子來(lái)更新每次迭代每個(gè)粒子新生產(chǎn)的位置以使粒子跳出局部?jī)?yōu)值。融合了標(biāo)準(zhǔn)微粒群算法和差分進(jìn)化算法優(yōu)點(diǎn)的混合算法加速了粒子的收斂速度。為了避免懲罰因子的選擇對(duì)實(shí)驗(yàn)結(jié)果的影響,采取了可行規(guī)則法來(lái)處理約束優(yōu)化問(wèn)題。最后將微粒群差分算法用于5個(gè)基準(zhǔn)函數(shù)和兩個(gè)工程問(wèn)題,并與其他算法作了比較,試驗(yàn)結(jié)果表明,微粒群差分算法算法具有很好的精準(zhǔn)性、魯棒性和有效性。
關(guān)鍵詞: 混合算法;約束優(yōu)化問(wèn)題;微粒群算法;差分進(jìn)化;可行規(guī)則
進(jìn)化算法由于其通用性、可靠性、穩(wěn)定性、簡(jiǎn)單性、所需要的信息少等一系列的優(yōu)點(diǎn),被廣泛地用來(lái)解決并且成功地解決了很多約束優(yōu)化問(wèn)題。因此,提出了很多基于進(jìn)化算法的約束處理方法[1-3]。由Kennedy和Eberhart [4] 提出的標(biāo)準(zhǔn)微粒群算法(PSO)便是其中一種應(yīng)用廣泛的仿生算法,它模擬鳥(niǎo)類(lèi)群體覓食行為來(lái)尋求最優(yōu)解,是一種基于群體智能的隨機(jī)尋優(yōu)算法,依賴(lài)于個(gè)體之間和種群之間的信息共享交換。然而PSO算法由于其種群的單一性容易導(dǎo)致早熟現(xiàn)象,使得優(yōu)化問(wèn)題陷入局部最優(yōu)解。利用其他算法的全局搜索能力來(lái)改善PSO算法的缺點(diǎn),這一混合算法的思想受到很多人的認(rèn)同,本文正是在此基礎(chǔ)上融合了差分進(jìn)化算法(DE)的進(jìn)化策略,提出了一種新的PSO、DE混合算法。算法的前半部分同粒子群算法,只是在粒子進(jìn)行速度、位置更新后,借鑒DE算法的變異、交叉、選擇算子以增強(qiáng)粒子群的多樣性。
1 背景知識(shí)介紹
1.1 PSO算法
如上所述,PSO是受鳥(niǎo)類(lèi)覓食行為啟發(fā)而來(lái)的隨機(jī)全局優(yōu)化算法。基本PSO的速度和位置更新方程如下:

其中, 為第i個(gè)粒子在第t次迭代時(shí)的自身歷史最優(yōu)位置,gbestt是第t次迭代時(shí)的種群最優(yōu)位置。
為第i個(gè)粒子在第t次迭代時(shí)的自身歷史最優(yōu)位置,gbestt是第t次迭代時(shí)的種群最優(yōu)位置。 是慣性權(quán)重,c1,c2是常量,r1,r2是服從U(0,1)的兩個(gè)相互獨(dú)立的隨機(jī)數(shù)。然而這個(gè)基本的PSO算法,速度是受到限制的。Clerc和Kennedy[5]引入了收縮因子
是慣性權(quán)重,c1,c2是常量,r1,r2是服從U(0,1)的兩個(gè)相互獨(dú)立的隨機(jī)數(shù)。然而這個(gè)基本的PSO算法,速度是受到限制的。Clerc和Kennedy[5]引入了收縮因子 修改了標(biāo)準(zhǔn)的微粒群模型,速度更新公式變?yōu)椋?/p>
修改了標(biāo)準(zhǔn)的微粒群模型,速度更新公式變?yōu)椋?/p>
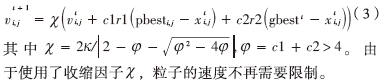
1.2 差分進(jìn)化算法(DE)
差分進(jìn)化算法是由Storn和Price[6]于1995年提出的解決全局優(yōu)化問(wèn)題的隨機(jī)進(jìn)化算法。算法通過(guò)變異、交叉、選擇3種操作來(lái)領(lǐng)導(dǎo)種群找到最優(yōu)解。DE算法的主要流程如下:
變異操作:本文中采用的是rand/1變異策略即vi=xr1+F×(xr2-xr3),{xr1, xr2, xr3}, 是在父代種群中隨機(jī)選擇的3個(gè)不同個(gè)體,并且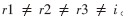 。F是一個(gè)介于[0,2]間的實(shí)型常量因子,稱(chēng)為放縮因子。
。F是一個(gè)介于[0,2]間的實(shí)型常量因子,稱(chēng)為放縮因子。
交叉操作:交叉操作的目的是通過(guò)變異個(gè)體Vi=(vi,1,vi,2,…,viD)和目標(biāo)個(gè)體Xi=(xi,1,xi,2,…,xiD)各維分量的隨機(jī)重組以提高種群個(gè)體的多樣性。算法通過(guò)下面的公式產(chǎn)生交叉向量Ui=(ui,1,ui,2,…,uiD):

其中,rand是[0,1]間的隨機(jī)數(shù);CR是范圍在[0,1]間的常數(shù)稱(chēng)為交叉變量。
選擇操作:在貪婪準(zhǔn)則的指導(dǎo)下,交叉向量Ui與目標(biāo)個(gè)體Vi競(jìng)爭(zhēng)。假設(shè)待求問(wèn)題為minf(x),則選擇操作可由下式確定:

1.3 可行規(guī)則
本文對(duì)于約束的處理采用的是可行規(guī)則法,可行規(guī)則[7]包含3個(gè)方面的內(nèi)容。
⑴任意可行解總是優(yōu)于不可行解;
⑵兩個(gè)不可行解之間,適應(yīng)值好的要優(yōu)于適應(yīng)值差的;
⑶兩個(gè)不可行解之間,約束沖突值小的要優(yōu)于約束沖突值大的。
總而言之,可行規(guī)則法就是找一個(gè)離可行域最近的解,即使這個(gè)解不在可行域內(nèi)。
2 微粒群差分算法(CPSODE)
2.1 CPSODE算法的原理
如上所述,基本PSO算法盡管操作簡(jiǎn)單但并不是完美的。在本文中,在PSO的基本框架中加入了DE進(jìn)化策略。基本PSO算法中的粒子在每次迭代中通過(guò)學(xué)習(xí)自身的歷史最優(yōu)位置和全局最優(yōu)位置來(lái)更新自己的速度和位置,從而慢慢靠近優(yōu)化問(wèn)題的最優(yōu)解。換句話說(shuō),PSO算法以全局最優(yōu)位置為中心,吸引所有其他粒子靠近,但是如果最優(yōu)位置粒子得不到更新,將出現(xiàn)早熟現(xiàn)象。這就是PSO算法陷入局部?jī)?yōu)值最本質(zhì)的原因。眾所周知,DE算法有著高效的全局搜索能力,其進(jìn)化策略不僅參數(shù)少而且收斂速度快。如果考慮在PSO的位置更新后,對(duì)位置矢量進(jìn)行DE的變異、交叉、選擇操作,在這里變異選取了rand/1策略,這樣位置矢量就得到更新,使得粒子的運(yùn)動(dòng)軌跡偏離既定的軌道,從而全局最優(yōu)位置得到更新,增強(qiáng)了種群多樣性。對(duì)DE進(jìn)化策略的采納不但加強(qiáng)了算法的搜索能力使算法能夠更快的收斂到最優(yōu)值,而且使算法跳出局部最優(yōu)值的概率很大,可以有效地避免早熟早收斂。
2.2 CPSODE算法的流程
為了處理約束,首先在搜索空間隨機(jī)初始化種群規(guī)模為M的粒子群的位置和速度,并計(jì)算每個(gè)粒子的適應(yīng)值和約束沖突值,令每個(gè)粒子的歷史最優(yōu)位置(記作pbest)為初始化位置,適應(yīng)值最優(yōu)的歷史最優(yōu)位置為種群最優(yōu)位置(記作gbest);其次根據(jù)式⑵、式⑶更新每個(gè)粒子的位置和速度,接著對(duì)更新的位置進(jìn)行DE算法的變異、交叉、選擇操作,并重新計(jì)算各個(gè)粒子的適應(yīng)值和約束沖突值;然后,在可行規(guī)則法的指導(dǎo)下,每個(gè)粒子更新pbest,并與gbest的適應(yīng)值進(jìn)行比較,若較好,則更新gbest,否則保持gbest原始位置。最后循環(huán)條件判斷,若不滿足算法會(huì)一次次迭代,直到滿足終止條件。程序的結(jié)構(gòu)流圖如圖1所示。
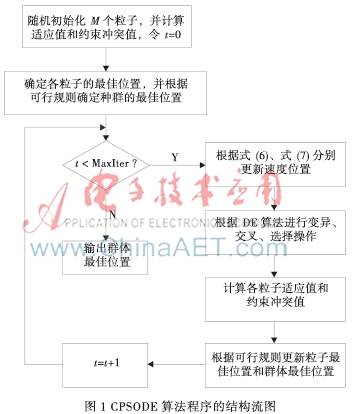
本文對(duì)于兩處位置更新也做了細(xì)節(jié)的處理。搜索在搜索范圍內(nèi)才是有效的,因此CPSODE算法為了避免對(duì)速度的限制,使用了帶收縮因子的速度更新公式即式(3),這樣就保證粒子每次迭代的速度都不會(huì)致使粒子偏離搜索范圍。其次,每次迭代新生產(chǎn)的位置若超出了邊界,則超出邊界的變量將用如下的法則處理[8]:

對(duì)每次迭代中DE交叉操作產(chǎn)生的交叉?zhèn)€體Uit,如果交叉?zhèn)€體Uit中任意一維向量Uti,j超出搜索空間,那么將會(huì)根據(jù)參考文獻(xiàn)[9]處理:
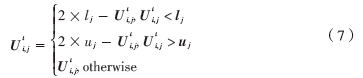
2.3 CPSODE算法時(shí)間復(fù)雜度分析
針對(duì)約束優(yōu)化問(wèn)題,設(shè)n為種群的粒子數(shù),d為目標(biāo)函數(shù)的維數(shù),T為最大迭代次數(shù)。根據(jù)圖1所示的CPSODE算法程序結(jié)構(gòu)流程來(lái)分析其復(fù)雜度。分析結(jié)果如表1所示。

由上表可以看出,CPSODE算法的復(fù)雜度是O(T×n)數(shù)量級(jí),n表示任意一個(gè)數(shù)。
3 實(shí)驗(yàn)仿真與分析
為了驗(yàn)證CPSODE算法的有效性,證明其相對(duì)于其他算法的優(yōu)點(diǎn),這一部分用了5 個(gè)典型約束測(cè)試函數(shù)和兩個(gè)實(shí)際的工程問(wèn)題來(lái)驗(yàn)證本文所提出的混合算法,這些測(cè)試函數(shù)包括非線性和二次函數(shù)。
3.1 典型約束測(cè)試函數(shù)優(yōu)化
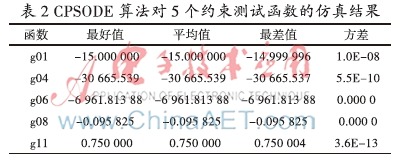
對(duì)每個(gè)測(cè)試函數(shù)獨(dú)立運(yùn)行100次,CPSODE算法參數(shù)設(shè)置如下:粒子數(shù)N=200,F(xiàn)和CR分別為0.4、0.9,g01,g04,g11最大迭代次數(shù)設(shè)置為500,g04和g08分別設(shè)置為300和250。收縮因子missing image file,對(duì)函數(shù)g11取 ε值為0.000 01。加速常量c1=c2=2.05。表2總結(jié)了在以上參數(shù)設(shè)置下約束測(cè)試函數(shù)的結(jié)果,給出了最好值,平均值,最差值和標(biāo)準(zhǔn)方差。可以看到CPSODE算法均能找到測(cè)試函數(shù)的全局最優(yōu)值,而且函數(shù)g06、g08能夠保持收斂到全局最優(yōu)值。每個(gè)測(cè)試函數(shù)獨(dú)立運(yùn)行100次的標(biāo)準(zhǔn)方差也比較小。
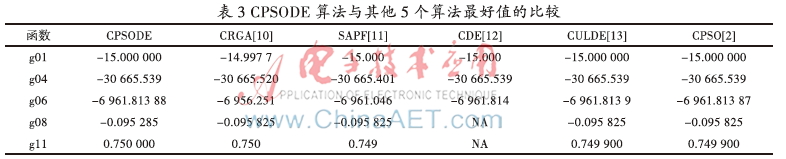


CPSODE算法同時(shí)也跟CRGA、SAPF、CDE、CLUDE和CPSO算法作了比較。結(jié)果如表3、表4、表5所示,NA表示不可求。從表格中可以看出,CPSODE算法要優(yōu)于CRGA、SAPF、CDE算法,且可與性能很好的CLUDE和ABC算法相比較。就CLUDE算法而言,本文所提出的算法對(duì)g11尋找到更好的最好值、平均值和最差值;針對(duì)g01函數(shù)的平均值和最差值,CPSODE算法結(jié)果比其結(jié)果要好;對(duì)剩下的函數(shù)CPSODE、CLUDE算法都可以找到相同的最好值,對(duì)g04、g06、g08這3個(gè)函數(shù)的平均值也相同,最差值方面兩種算法對(duì)g06、g08的最差值相同,只是對(duì)g04函數(shù)的最差值,CPSODE要略遜色一些。對(duì)于CPSO算法,CPSODE算法對(duì)g11函數(shù)求得的最好值、平均值、最差值都要優(yōu)于CPSO算法。總而言之,CPSODE算法具有較好的尋優(yōu)能力。
3.2 工程問(wèn)題優(yōu)化
為了研究CPSODE算法解決現(xiàn)實(shí)生活中工程問(wèn)題的性能,用兩個(gè)典型的實(shí)際工程問(wèn)題對(duì)算法做了測(cè)試,分別是焊接條和伸縮繩問(wèn)題。每個(gè)問(wèn)題獨(dú)立運(yùn)行100次,粒子數(shù)N=200,F(xiàn)和CR分別為0.4、0.9,最大迭代次數(shù)設(shè)置為500。

從表6可以看出,CPSODE找到的最優(yōu)解比參考文獻(xiàn)[15]、參考文獻(xiàn)[16]結(jié)果要好。而且CPSODE算法的平均值比其他算法都好,不僅如此,最差值和方差都是最優(yōu)的。甚至CPSODE的最差值也要比參考文獻(xiàn)[16]最優(yōu)值好。表明CPSODE對(duì)于實(shí)際工程問(wèn)題的求解有其明顯的優(yōu)勢(shì)。
從表7中,可以得出CPSODE算法找到的最優(yōu)值比參考文獻(xiàn)[16]、參考文獻(xiàn)[17]結(jié)果好,不僅如此,本文所提出算法對(duì)伸縮繩問(wèn)題求解的平均值和方差均優(yōu)于其他算法,最差值也同樣優(yōu)于除了參考文獻(xiàn)[18]之外的其他算法,甚至要比參考文獻(xiàn)[17]最優(yōu)值要好。
3.3 CPSODE搜索效率分析

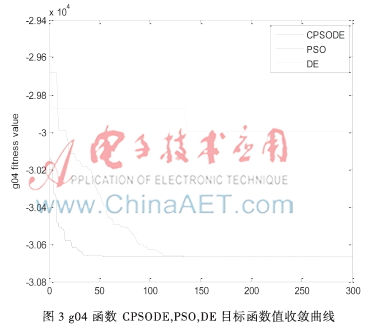
圖2和圖3 分別說(shuō)明了g01、g04這兩個(gè)函數(shù)收斂到目標(biāo)函數(shù)最優(yōu)值的迭代過(guò)程,從兩幅圖中可以看出CPSODE比PSO、DE能更快地找到最優(yōu)適應(yīng)值。由于混合了DE算法,不僅找到全局最優(yōu)值而且加快了收斂速度。因此,證實(shí)了本文所提出的算法具有良好的全局搜索能力。
本文提出了一種新的算法,并命名為CPSODE算法,該算法通過(guò)嵌入DE算法提高了單一PSO算法的性能。算法通過(guò)局部最優(yōu)值pbest和全局最優(yōu)值gbest引導(dǎo)粒子最終收斂到全局最優(yōu)位置,并在可行規(guī)則的指導(dǎo)下[7]來(lái)比較粒子更新的位置和其相對(duì)應(yīng)的歷史最優(yōu)位置,然后優(yōu)勝者更新pbest。在本文的后部分進(jìn)一步的運(yùn)用了CPSODE算法對(duì)5個(gè)典型的約束測(cè)試函數(shù)和兩個(gè)典型的約束優(yōu)化工程問(wèn)題進(jìn)行了實(shí)驗(yàn)仿真,并對(duì)其收斂性和復(fù)雜度進(jìn)行了分析。從比較的研究中可以看出CPSODE展現(xiàn)了其對(duì)約束優(yōu)化問(wèn)題良好的求解性能。新提出的算法改善了PSO算法的魯棒性。
參考文獻(xiàn)
[1] Mohamed A W, Sabry H Z. Constrained optimization based on modified differential evolution algorithm[J].Information Science,2012(194):171-208.
[2] Daneshyari, M, Yen, G.G. Constrained multiple-swarm particle swarm optimization within a cultural framenwork[J].Transactions on Systems,Man and Cybernetics,Part A: Systems and Humans,2012,42(2):475-490.
[3] Gandomi A H,Yang Xinshe, Alavi A H. Cuckoo search algorithm: a metaheuristic approach to solve structural optimization problems[J].Engineering with Computers,2013,29(1):17-35.
[4] Eberhart R, Kennedy J.A new optimizer using particle swarm theory[C].Sixth International Symposium on Micro machine and Human Science, Nagoya,1995:39-43.
[5] Clerc M . Kennedy J. The particle swarm- explosion,stability,and convergence in amultidimensional complex space[J]. IEEE Transactions on Evolutionary Computation ,2002,6(1) :58-73.
[6] Rainer S, Kenneth P.Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J].Journal of global optimization ,1997,11(4) :341-359.
[7] Kalyanmoy D.An efficient constraint handling method for genetic algorithms[J].Computer Methods in Applied Mechanics and Engineering ,2000,186(2-4): 311-338.
[8] Zielinski K, Laur R. Constrained single-objective optimization using differential evolution [C].IEEE Congress on Evolutionary Computation,Vancouver,BC:IEEE, 2006:223-230.
[9] Kukkonen S, Lampinen J. Constrained real-parameter optimization with generalized differential evolution [C].IEEE Congress on Evolutionary Computation, Vancouver, BC:IEEE,2006:207-214.
[10] Amirjanov A.The development of a changing range genetic algorithm[J]. Computer Methods in Applied Mechanics and Engineering ,2006,195(19-22):2495-2508.
[11] Tessema B,Yen G.G A self-adaptive penalty function based algorithm for constrained optimization[C]. IEEE Congress on Evolutionary Computation,Vancouver, BC:IEEE,2006:246-253.
[12] Huang Fuzhuo, Wang Ling, He Qie.An efficient co-evolutionary differential evolution for constrained optimization[J]. Applied Mathematics and Computation, 2007,186(1):340-356.
[13] Becerra R L,Carlos A. Coello Coello.Cultured differential evolution for constrained optimization[J].Computer Methods in Applied Mechanics and Engineering, 2006,195(33-36): 4303-4322.
[14] Akay B, Karaboga D.Artificial bee colony algorithm for large-scale problems and engineering design optimization[J].Journal of Intelligent Manufacturing, 2012,23(4): 1001-1014.
[15] Eskandar H,Sadollah A,Bahreininejad A,et al.Water cycle algorithm-A novel metaheuristic optimization method for solving constrained engineering optimization problems[J].Computer and Structures.,2012(110-111):151-166.
[16] He Qie, Wang Ling.An effective co-evolutionary particle swarm optimization for constrained engineering design problems[J].Engineering Applications of Artificial Intelligence,2007,20(1):89-99.
[17] Coello C C, Becerra RL. Efficient evolutionary optimization through the use of a culture algorithm[J]. Engineering Optimizaiton,2004,36(2): 219-236.

