0 引言

　　數(shù)學模型是整流器控制算法仿真的基礎(chǔ),，根據(jù)不同的控制需要可以建立不同的數(shù)學模型,。本文除了研究整流器數(shù)學模型之外，還介紹了基于不同坐標系數(shù)學模型的坐標變換,、單位功率因數(shù)的定義、PWM 整流器四象限運行原理等與整流器控制算法仿真相關(guān)的一般性的問題,。

1 三相電壓型整流器數(shù)學模型

　　1.1 三相電壓型整流器一般數(shù)學模型

　　所謂三相電壓型整流器一般數(shù)學模型就是根據(jù)三相電壓型整流器拓撲結(jié)構(gòu),，在三相靜止坐標系（a，b,，c）中,，利用電路基本定律（基爾霍夫電壓、電流定律）對三相電壓型整流器所建立的一般數(shù)學描述,。三相電壓型整流器拓撲結(jié)構(gòu)如圖1所示,。

　　該數(shù)學模型在以下假設條件下建立：

　　1）電網(wǎng)電動勢為三相平穩(wěn)的純正弦波電動勢（ea，eb,，ec）,；

　　2）網(wǎng)側(cè)濾波電感L 是線性的，且不考慮其飽和狀況,；

　　3）功率開關(guān)管損耗以電阻Rs表示,，即實際的功率開關(guān)管可以用理想開關(guān)與損耗電阻Rs 串聯(lián)等效來表示,；

　　4）為描述整流器能量的雙向傳輸，整流器直流側(cè)負載由電阻RL和直流電動勢eL串聯(lián)表示,。

　　根據(jù)三相電壓型整流器特性分析需要,，其一般數(shù)學模型的建立可采用以下兩種形式：

　　1）采用開關(guān)函數(shù)描述的一般數(shù)學模型；

　　2）采用占空比描述的一般數(shù)學模型,。

　　采用開關(guān)函數(shù)描述的一般數(shù)學模型是對整流器開關(guān)過程的精確描述,，較適合于整流器的波形仿真，因此本文所述的整流器系統(tǒng)仿真是采用開關(guān)函數(shù)描述的數(shù)學模型,。下面以三相整流器拓撲結(jié)構(gòu)為例,，建立采用開關(guān)函數(shù)描述的一般數(shù)學模型。

　　為分析方便,，首先定義單極性二值邏輯開關(guān)函數(shù)sk為

　　將整流器的功率開關(guān)管損耗等效電阻Rs 同交流濾波電感等效電阻RI合并,，且令R=Rs+RI，采用基爾霍夫電壓定律建立三相整流器的a相回路方程為

　　1.2 三相電壓型整流器d-q 模型

　　三相靜止對稱坐標系下的一般數(shù)學模型具有物理意義清晰,、直觀等特點,。但是這種數(shù)學模型中，整流器交流側(cè)均為時變交流量,，因而不利于控制系統(tǒng)的設計,。為此，可以通過坐標變換將三相對稱靜止坐標系（a,，b,，c）轉(zhuǎn)換成以電網(wǎng)基波頻率同步旋轉(zhuǎn)的（d，q）坐標系,。這樣,，經(jīng)坐標旋轉(zhuǎn)變換后，三相對稱靜止坐標系中的基波正弦交流變量將轉(zhuǎn)化成同步旋轉(zhuǎn)坐標系中的直流變量,，從而簡化了對控制系統(tǒng)的設計,。

　　三相整流器一般數(shù)學模型經(jīng)同步旋轉(zhuǎn)坐標變換后，即轉(zhuǎn)換成三相整流器d-q 模型,。

　　要實現(xiàn)從三相靜止坐標系（a,，b，c）到兩相同步旋轉(zhuǎn)坐標系（d,，q）的變換,，必須首先確定坐標系（d，q）的空間位置,。如圖2 所示,，在三相靜止坐標系（a，b，c）中,，E,、I 分別表示三相電網(wǎng)電動勢矢量和電流矢量，并且E,、I 以電網(wǎng)基波角頻率棕逆時針旋轉(zhuǎn),。根據(jù)瞬時無功功率理論,，在描述三相電量時,，為簡化分析,，將兩相旋轉(zhuǎn)坐標系（d,，q）中q 軸與電網(wǎng)電動勢矢量E同軸,。即q 軸按矢量E定向,，矢量E（q 軸）方向的電流分量iq定義為有功電流,，而比矢量E 滯后90毅相角的軸（d軸）方向電流分量id定義為無功電流,。另外,，初始條件下,，令q 軸與a軸重合。

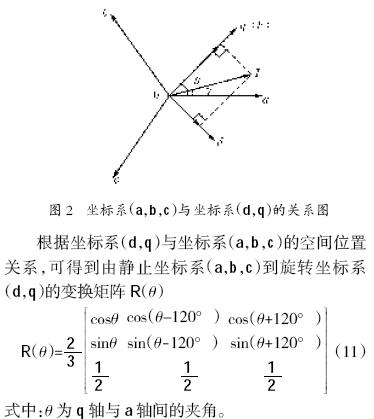
　　1.3 坐標變換在Matlab/Simulink中的實現(xiàn)

　　從三相靜止坐標系（a,，b,，c）到兩相同步旋轉(zhuǎn)坐標系（d，q）的變換是算法仿真中重要的模塊之一,?；Ｗ兘Y(jié)構(gòu)電流控制算法本身就是基于兩相同步旋轉(zhuǎn)

　　坐標系的；滯環(huán)SVPWM 算法雖然是基于三相靜止坐標系的,，但是在對電流控制效果的分析中也用到了坐標變換模塊,。在此將該模塊功能的實現(xiàn)方法做簡單介紹。

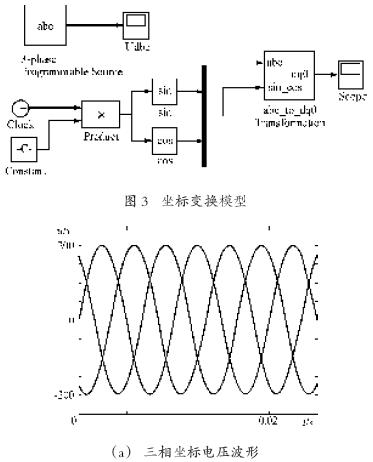
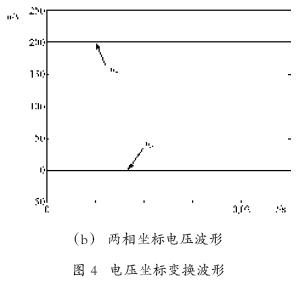
　　三相靜止坐標系到兩相任意旋轉(zhuǎn)坐標系的變換及其反變換已經(jīng)建立在Smulink 的power system 模型庫中,，提取路徑為power system blockset / extra library / measurements / abc_to_dq0 transformation（dq0_abc transformation）,。應用該模塊實現(xiàn)坐標變換的例子如圖3所示。仿真結(jié)果如圖4所示,，其中圖4（a）為變換前的三相電壓,，圖4（b）為經(jīng)坐標變換后旋轉(zhuǎn)兩相坐標系上的電壓波形，由于所選角頻率棕與電源角頻率同步,，所以在兩相同步旋轉(zhuǎn)坐標系上的電壓已經(jīng)是直流。

2 網(wǎng)側(cè)功率因數(shù)

　　功率因數(shù)是對電能進行安全有效利用的衡量標準之一,。目前,，功率因數(shù)校正技術(shù)走過了從無功功率補償?shù)綗o源、有源濾波,，再到有源功率因數(shù)校正和單位功率因數(shù)變換技術(shù)的發(fā)展歷程,。實現(xiàn)單位功率因數(shù)變換是應用各種控制算法對整流器進行控制的目的所在。

　　對電力電子變流裝置的網(wǎng)側(cè)功率因數(shù)的具體定義如下。

　　以單相電源為例,，設網(wǎng)壓無諧波且可表示為

3 PWM整流器四象限運行原理

　　圖5為PWM整流器模型電路,。從圖5中可以看出：PWM 整流器模型電路由交流回路、功率開關(guān)管橋路以及直流回路組成,。其中交流回路包括交流電動勢E以及網(wǎng)側(cè)電感L 等,；直流回路包括負載電阻RL及負載電動勢eL等。

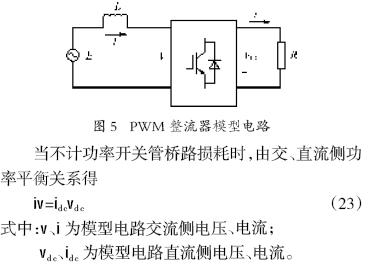
　　由式（23）知：通過對模型電路交流側(cè)的控制,，就可以控制其直流側(cè),，反之亦然。

　　穩(wěn)態(tài)條件下,，PWM 整流器交流側(cè)矢量關(guān)系如圖6所示,。當以電網(wǎng)電動勢矢量為參考時，通過控制交流電壓矢量V 即可實現(xiàn)PWM 整流器的四象限運行,。假設| I |不變,，因此| VL |=棕L| I |也固定不變；隨著交流電流矢量I 方向的變化,，PWM 整流器交流電壓矢量V 端點運動軌跡構(gòu)成了一個以|VL| 為半徑的圓,。進一步分析，可得PWM整流器四象限運行規(guī)律如下：

　　1）電壓矢量V 端點在圓軌跡A蓻B 上運動時,，PWM整流器運行于整流狀態(tài),。此時，PWM整流器需從電網(wǎng)吸收有功及感性無功功率,，電能將通過PWM 整流器由電網(wǎng)傳輸至直流負載,。當PWM整流器運行在B點時，則實現(xiàn)單位功率因數(shù)整流控制,。

　　2）當電壓矢量V端點在圓軌跡B蓻C上運動時,，PWM整流器運行于整流狀態(tài)。此時,，PWM 整流器需從電網(wǎng)吸收有功及容性無功功率,，電能將通過PWM 整流器由電網(wǎng)傳輸至直流負載。

　　3）當電壓矢量V 端點在圓軌跡C蓻D上運動時,，PWM整流器運行于有源逆變狀態(tài),。此時PWM整流器向電網(wǎng)傳輸有功及容性無功功率，電能將從PWM整流器直流側(cè)傳輸至電網(wǎng),。

　　4）當電壓矢量V 端點在圓軌跡D蓻A上運動時,，PWM整流器運行于有源逆變狀態(tài)。此時,，PWM整流器向電網(wǎng)傳輸有功及感性無功功率,，電能將從PWM整流器直流側(cè)傳輸至電網(wǎng)。

　　顯然，要實現(xiàn)PWM整流器的四象限運行,，關(guān)鍵在于網(wǎng)側(cè)電流的控制,。一方面，可以通過控制PWM整流器交流側(cè)電壓,，間接控制其網(wǎng)側(cè)電流,；另一方面，也可通過網(wǎng)側(cè)電流的閉環(huán)控制,，直接控制PWM整流器的網(wǎng)側(cè)電流,。本文所述控制算法均屬于后者。