摘  要： 為了提高極點提取的精度,，提出了一種利用小波包變換的軟閾值法去噪的改進(jìn)算法,，同時，利用矩陣束法提取極點。實驗結(jié)果表明,，在信噪比為6 dB的條件下,，仍然可以精確地提取極點并重構(gòu)瞬態(tài)信號，為無芯RFID標(biāo)簽的研究提供了重要參考,。
關(guān)鍵詞： 小波包分析,；矩陣束法；極點

　無芯RFID標(biāo)簽指的是一種不含有硅芯片的射頻卡,，與現(xiàn)有的有芯片RFID標(biāo)簽相比,，無芯標(biāo)簽更有可能降低其成本，主要潛在優(yōu)勢在于花費(fèi)0.1美分即可將其直接印在產(chǎn)品上,，有利于其占領(lǐng)市場份額,。依據(jù)目標(biāo)結(jié)構(gòu)的自然諧振特性，將它對超寬帶電磁脈沖的散射場通過奇點展開法映射成極點和留數(shù),，探討無芯標(biāo)簽結(jié)構(gòu)和極點與留數(shù)的關(guān)系,，已經(jīng)成為無芯RFID技術(shù)的研究熱點[1]。
　奇點展開法SEM(Singularity Expansion Method)[2]指出目標(biāo)的后時瞬態(tài)響應(yīng)可由一系列衰減的復(fù)指數(shù)信號之和來逼近,，啟發(fā)人們運(yùn)用極點的概念來表征目標(biāo)的特征,。極點作為目標(biāo)的固有屬性，只與目標(biāo)本身結(jié)構(gòu)有關(guān),，與外界因素?zé)o關(guān),，改變其結(jié)構(gòu)即可操作極點的大小和數(shù)目。對于RFID標(biāo)簽類的有限尺寸散射體,，極點提供了嵌入在標(biāo)簽中的對象數(shù)據(jù),，該數(shù)據(jù)可由對散射場進(jìn)行分析獲取，最終實現(xiàn)對目標(biāo)的識別,。
　長期以來,，人們對極點提取的研究從未間斷，相繼提出了Prony法,、KT法,、矩陣預(yù)測法、矩陣束法MPM(Matrix Pencil Method)[3]等,，其中以矩陣束法的應(yīng)用最為廣泛,。為了進(jìn)一步改善低信噪比條件下MPM方法極點提取的精度，本文對現(xiàn)有的矩陣束法進(jìn)行了改進(jìn),。首先,，利用快速小波包變換對含有噪聲的瞬態(tài)響應(yīng)數(shù)據(jù)進(jìn)行去噪處理；然后,，將得到的數(shù)據(jù)用矩陣束法提取極點,，對現(xiàn)有的矩陣束算法進(jìn)行了改進(jìn),；最后，通過仿真分析以及波形的重構(gòu),，驗證改進(jìn)算法的有效性,。
1 改進(jìn)的算法
　近年來，由于小波理論的不斷發(fā)展,，在實際工程問題中,，小波的應(yīng)用也越來越廣泛。小波包分析是小波變換的推廣,，它能對小波變換沒有細(xì)分的高頻部分進(jìn)行進(jìn)一步分解,，具有更為精確的局部分析能力，從而提高了時頻分辨率,。將小波包分析應(yīng)用于圖像以及瞬態(tài)信號去噪處理是當(dāng)前的研究熱門,。下面從數(shù)字濾波器的角度出發(fā)，闡述小波包變換的概念,。
1.1 小波包變換的原理
　小波包分析是從小波分析延伸出來的一種對信號進(jìn)行更加細(xì)致的分析和重構(gòu)的方法,。在多分辨率分析中，按照不同的尺度因子j把Hilbert空間L2(R)分解為

　對于小波包變換以及去噪原理,，參考文獻(xiàn)[4-5]有詳細(xì)的闡述,?？焖傩〔ò儞Q是著名的Mallat算法的延伸和推廣,，可以減少計算量，提高計算精度,。對信號分解時,，小波包不但對高頻細(xì)節(jié)進(jìn)行分解，而且也對低頻逼近也進(jìn)行分解,，因此,，小波包分解的樹形結(jié)構(gòu)圖是完整的。同樣,，信號的重構(gòu)的樹形結(jié)構(gòu)圖也是對應(yīng)的,。當(dāng)然，在工程應(yīng)用中,，完整的小波包分解是不必要的,，依照具體情況分解和重構(gòu)。這樣,，小波包分析在應(yīng)用中就有很大的靈活性,。
1.2 算法的描述
　在小波包分析領(lǐng)域，隨著分辨率尺度j的增加,，噪聲系數(shù)的幅值快速衰減,，而真實信號的特征越來越明顯,，系數(shù)基本不變，而噪聲相對越弱,。根據(jù)這一特征,，可先將信號進(jìn)行小波包分解，再設(shè)計一個門限閾值,，將低于該門限的小波包系數(shù)進(jìn)行相關(guān)處理,，然后將處理后的小波包系數(shù)重構(gòu)回原始數(shù)據(jù)，從而使信號中的隨機(jī)噪聲得到有效抑制,。
　本文針對瞬態(tài)信號的提取,，首先利用小波包分析對瞬態(tài)信號去噪處理，然后將得到的數(shù)據(jù)構(gòu)造漢克爾矩陣,，運(yùn)用矩陣束法提取極點,。為了進(jìn)一步提高極點的有效性和精確度，本文采取對小波包去噪后的數(shù)據(jù)進(jìn)行5次重復(fù)極點提取,，將5次結(jié)果的平均值作為最終極點,。圖1即為極點提取的改進(jìn)算法流程圖。
在小波包去噪方法的研究中,，本文將采取軟門限法,，其關(guān)鍵在于估計閾值和最優(yōu)小波基的選取。根據(jù)本文研究的對象是瞬態(tài)信號,，本文以Birge-massart準(zhǔn)則作為閾值估計準(zhǔn)則,，采用軟閾值法進(jìn)行量化處理，選取db4為最優(yōu)小波基,。   
2 改進(jìn)算法的仿真與分析
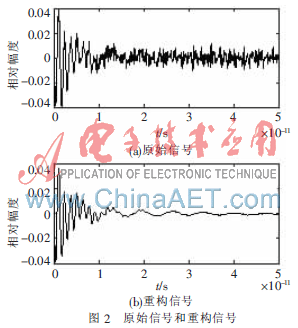
　為了驗證新算法的優(yōu)越性,，以參考文獻(xiàn)[6]中細(xì)直導(dǎo)體為對象，對其進(jìn)行極點提取仿真實驗,。由于極點和留數(shù)一般都是以共軛形式存在的,，因此取參考文獻(xiàn)[6]中前6個極點為理論值，如表1所示,。表1中的極點都是歸一化數(shù)據(jù)sL/c(L為導(dǎo)體長度1 m,，c代表光速)，然后在計算機(jī)中模擬信噪比為6 dB的目標(biāo)回波的后時瞬態(tài)響應(yīng),，如圖2所示,。其中，假設(shè)噪聲為高斯白噪聲,。在算法仿真中,，信號時域采樣間隔為?駐t=10-13s，時域信號長度為5×10-11s,，故采樣點為500,。

　為了更加直觀地體現(xiàn)改進(jìn)算法的先進(jìn)性,，本文同時將MTLS-MPM法[3]對同一目標(biāo)進(jìn)行極點提取。表1清晰地列出了兩算法得到的極點數(shù)據(jù),。
　從表1可知,，改進(jìn)算法的極點估計值比MTLS-MPM法的極點估計值更接近理論值。經(jīng)過相關(guān)計算,，前者的極點相對于理論值均方誤差為0.081 3,，后者為0.161 0。而圖2中的原始信號和重構(gòu)信號則更直觀地展現(xiàn)了改進(jìn)算法提取極點的精度,。

　在本算法驗證的過程中,，目標(biāo)回波后瞬態(tài)信號是由已知的理論極點值模擬仿真得到，因此故極點數(shù)目是確定的,。然而,，在實際的應(yīng)用中，極點的數(shù)目是無法預(yù)先得知的,，只可能事先根據(jù)經(jīng)驗推測得到,。如果極點數(shù)目取值過大或取值過小都會引起誤差。另外,，實際信號中的噪聲是未知的,，所以本文提出的算法要想實際應(yīng)用，還需解決這些問題,。
　因此,，結(jié)構(gòu)不同的無芯RFID標(biāo)簽所對應(yīng)的極點和留數(shù)也是異樣的，這相當(dāng)于有芯RFID標(biāo)簽的唯一標(biāo)識符,，具有異同性,。如果將有用數(shù)據(jù)嵌入其中,，使調(diào)制的散射回波具有規(guī)律性,，從而得到預(yù)期的散射場，利用本文極點提取的算法,，可獲得準(zhǔn)確的極點,，最終讀寫器成功識別標(biāo)簽。現(xiàn)在的關(guān)鍵點是研究輕級量高效的極點提取算法和無芯標(biāo)簽結(jié)構(gòu)的設(shè)計,。這含有巨大潛在的商機(jī),，值得進(jìn)一步研究。
　本文提出了基于小波包變換理論和矩陣束法理論的目標(biāo)極點提取算法,，該算法的有效性在計算機(jī)仿真結(jié)果中得到驗證,。雖然小波包分析可以有效地去噪，運(yùn)用現(xiàn)有的極點數(shù)目判別準(zhǔn)則確定M有一定的幫助,，但在實際應(yīng)用過程中,，極點數(shù)目確定環(huán)節(jié)還有待于進(jìn)一步改進(jìn),，這也是接下來的研究重點。從重構(gòu)信號波形圖,、極點估計值與理論值的趨近度比較角度看,，該算法均優(yōu)于傳統(tǒng)的TLS-MPM算法。另外,，在信噪比為6 dB的情況下,，本文提出的算法依然能精確地估計出信號的極點值并進(jìn)行波形重構(gòu)，并對隨機(jī)高斯噪聲具有很好的抑制作用,，這對于無芯RFID技術(shù)的研究有一定的參考價值,。
參考文獻(xiàn)
[1] BALBIN I， KARMAKAR C N. Phase-encoded chipless RFID tansponder for large-scale low-cost applications[J]. IEEE Microwave and Wireless Components Letters,， 2009,，19(8)：509-511.
[2] MUKHERJEE S. Chipless radio frequency identification by remote measurement of complex impedance[C]. European Microwave Conference Munich， 2007,，1007-1010.
[3] 伍光新.諧振區(qū)雷達(dá)目標(biāo)特征提取與目標(biāo)識別研究[D].哈爾濱：哈爾濱工業(yè)大學(xué),，2008：47-50.
[4] 唐曉初.小波分析及其應(yīng)用[M].重慶：重慶大學(xué)出版社，2006.
[5] Chen Xiaojing,， Wu Di. An effective signal algorithm combining optimal wavelet packet basic and translation-invariant algorithm[J]. IEEE Congress on Image and Signal Processing,， 2008，4(13)： 275-279.
[6] MOONEY J E,， RIGGS L S. Robust target identification in white Gaussian noise for ultra wide-band radar systems[C]. IEEE Transactions on Antennas and Propagation,， 1998， 46(12)：1823-1827.