摘 要: 針對(duì)資源受限項(xiàng)目調(diào)度問題,提出了一種基于人工蜂群算法的優(yōu)化方法。人工蜂群算法中每個(gè)食物源的位置代表一種項(xiàng)目任務(wù)的優(yōu)先權(quán)序列,每個(gè)食物源的位置通過擴(kuò)展串行調(diào)度機(jī)制轉(zhuǎn)換成可行的調(diào)度方案,迭代中由三種人工蜂執(zhí)行不同的操作來(lái)實(shí)現(xiàn)全局最優(yōu)解的更新。實(shí)驗(yàn)結(jié)果表明,人工蜂群算法是求解資源受限項(xiàng)目調(diào)度問題的有效方法,同時(shí)擴(kuò)展調(diào)度機(jī)制的引入可以加速迭代收斂的進(jìn)程。
關(guān)鍵詞: 資源受限項(xiàng)目調(diào)度;人工蜂群算法;擴(kuò)展串行調(diào)度
現(xiàn)代項(xiàng)目管理的理念和方法已經(jīng)被越來(lái)越多的組織所接受,成為組織模式中不可或缺的一部分,而項(xiàng)目調(diào)度是項(xiàng)目管理中最具挑戰(zhàn)行性的工作。由于項(xiàng)目的可用資源稀缺及項(xiàng)目任務(wù)間的必須滿足的工序關(guān)系,使得項(xiàng)目調(diào)度成為一個(gè)十分復(fù)雜的問題。資源受限的項(xiàng)目調(diào)度RCPSP(Resource-Constrained Project Scheduling)問題是一類典型的組合優(yōu)化問題,在理論上Blazewicz[1]已經(jīng)證明它屬于強(qiáng)NP-hard問題,對(duì)于大規(guī)模的項(xiàng)目調(diào)度采用精確解法求解就變得十分困難,而啟發(fā)式算法在求解速度上則表現(xiàn)出明顯的優(yōu)越性。近年來(lái)國(guó)內(nèi)外學(xué)者對(duì)基于優(yōu)先規(guī)則的啟發(fā)式算法做了大量的研究,先進(jìn)進(jìn)化和智能算法不斷出現(xiàn)(如模擬退火算法、禁忌搜索算法、遺傳算法,及蟻群算法、粒子群算法等),并被逐步應(yīng)用到RCPSP問題求解中。
受到蜜蜂群體采蜜行為的啟發(fā),2005年Karaboga[2]提出了一種基于蜂群智能的新的人工蜂群算法ABC(Artificial Bee Colony)。Karaboga等[3-4]已經(jīng)驗(yàn)證與遺傳算法、差分進(jìn)化算法及粒子群算法相比,ABC算法在連續(xù)型多峰函數(shù)尋優(yōu)問題中能得到更好的結(jié)果。ABC算法是連續(xù)性問題優(yōu)化提出的,在離散性問題,如組合優(yōu)化等問題中的應(yīng)用還比較少。
本文根據(jù)資源受限項(xiàng)目調(diào)度問題的解的特點(diǎn),提出了一種基于優(yōu)先權(quán)的求解RCPSP的人工蜂群算法,并通過實(shí)例仿真驗(yàn)證了算法的有效性。
1 問題描述
典型的資源受限項(xiàng)目調(diào)度問題基于下述假設(shè):(1)組成項(xiàng)目的各任務(wù)是確定的,且工期已知;(2)每項(xiàng)任務(wù)必須在其所有的緊前任務(wù)完成后方能開始;(3)項(xiàng)目的可用資源為多種可更新資源,已知資源可用量的最大限額且在項(xiàng)目整個(gè)過程中保持不變;(4)任務(wù)不可拆分,即任務(wù)一旦開始不得中斷;(5)調(diào)度的優(yōu)化目標(biāo)是項(xiàng)目工期最短。因此,RCPSP可描述為:設(shè)項(xiàng)目的任務(wù)集為J={0,1,2,…,n,n+1},其中任務(wù)0和n+1為虛任務(wù),工期為0,分別代表開始任務(wù)和結(jié)束任務(wù)。sj=fj-dj,C={(i,j)|i必須在j開始前完成}為項(xiàng)目的緊前任務(wù)集,其中sj、fj、dj分別表示第j項(xiàng)任務(wù)的開始時(shí)間、結(jié)束時(shí)間和總耗時(shí)。設(shè)項(xiàng)目共有K種可更新資源,第k種資源的總量為Rk,第j項(xiàng)任務(wù)對(duì)第k種資源的需求量為rjk。則資源受限的項(xiàng)目調(diào)度的數(shù)學(xué)模型為:

2 人工蜂群算法求解RCPSP
2.1 人工蜂群算法簡(jiǎn)介
人工蜂群算法是一種基于群智能的元啟發(fā)算法,因其原理簡(jiǎn)單易于實(shí)現(xiàn)的特點(diǎn)受到了越來(lái)越多的關(guān)注。人工蜂群算法中有兩個(gè)重要組成:人工蜜蜂和食物源。人工蜜蜂分為三類:工作蜂、跟隨蜂和偵查蜂,每一種人工蜂扮演不同的角色。工作蜂在蜜源采蜜,并將蜜源信息帶回與跟隨蜂分享;跟隨蜂等候在蜂巢從回來(lái)的工作蜂那里得到食物源的信息;偵查蜂負(fù)責(zé)尋找新蜜源。工作蜂通過在蜂巢跳舞場(chǎng)以“擺尾舞”的方式分享信息,其舞蹈形態(tài)和采蜜蜜源的蜂蜜量成正比。跟隨蜂觀察舞蹈,然后依據(jù)分享蜜源的蜂蜜量選擇適當(dāng)?shù)氖澄镌矗妹墼磳?huì)吸引更多的跟隨蜂。當(dāng)一個(gè)蜜源被多次采蜜后,就會(huì)被拋棄,然后偵查蜂就會(huì)勘探另一個(gè)新蜜源。因此,偵查蜂的作用可以看做是開發(fā)食物源,而工作蜂和跟隨蜂的作用是開采食物源。蜂群按數(shù)量等分成兩組,前一半是工作蜂,后一半是跟隨蜂。每一個(gè)工作蜂對(duì)應(yīng)一個(gè)食物源,即工作蜂的數(shù)目和蜂巢周圍的食物源的數(shù)目相等。在ABC算法中食物源即蜜源,每個(gè)食物源的位置代表優(yōu)化問題的一個(gè)可行解,食物源的蜂蜜量稱為適應(yīng)值,代表相關(guān)解的質(zhì)量。
2.2 人工蜂群算法求解RCPSP
本文ABC算法的基礎(chǔ)采用基于優(yōu)先權(quán)編碼的人工蜂群算法對(duì)RCPSP進(jìn)行求解。
2.2.1 基于優(yōu)先權(quán)的食物源位置編碼
在ABC算法中,每個(gè)食物源的位置代表一個(gè)可行解。在用ABC算法求解資源受限項(xiàng)目調(diào)度問題時(shí),每個(gè)食物源的位置xi是一個(gè)n維向量,取xi=(xi1,xi2,…,xid,…,xin),向量的維數(shù)n即是項(xiàng)目的非虛擬任務(wù)數(shù)。食物源xi代表一種項(xiàng)目任務(wù)的優(yōu)先權(quán)序列。其中,xid是第i個(gè)食物源的第d個(gè)位置的值,它對(duì)應(yīng)了第d項(xiàng)任務(wù)的優(yōu)先權(quán)為xid。ABC算法得到的xi是連續(xù)數(shù)構(gòu)成的向量,通過把xi向量元素按從小到大排序,轉(zhuǎn)換成1~n的整數(shù)排列。這種整數(shù)優(yōu)先權(quán)序列再通過調(diào)度生成機(jī)制轉(zhuǎn)換為一個(gè)可行的調(diào)度方案。
2.2.2 適應(yīng)值函數(shù)
ABC算法中食物源的好壞用蜂蜜量的多少來(lái)衡量,蜂蜜量是指食物源對(duì)應(yīng)的可行解的適應(yīng)值函數(shù)。在RCPSP中食物源對(duì)應(yīng)了項(xiàng)目任務(wù)的優(yōu)先權(quán)序列,優(yōu)先權(quán)序列可以通過調(diào)度生成機(jī)制轉(zhuǎn)換成可行調(diào)度方案,每一調(diào)度方案對(duì)應(yīng)了項(xiàng)目工期。RCPSP優(yōu)化目標(biāo)是使項(xiàng)目工期最短,并意味著解的質(zhì)量越好,因此ABC算法中食物源xi的適應(yīng)值fiti。可由式(4)轉(zhuǎn)換得到。

2.2.3 擴(kuò)展串行調(diào)度生成機(jī)制
一個(gè)食物源的位置編碼對(duì)應(yīng)了項(xiàng)目的一種任務(wù)優(yōu)先權(quán)序列,需要通過適當(dāng)?shù)恼{(diào)度生成機(jī)制把任務(wù)的優(yōu)先權(quán)轉(zhuǎn)化為可行的調(diào)度方案,本文采用擴(kuò)展的串行調(diào)度生成機(jī)制[5]來(lái)生成可行調(diào)度方案。串行調(diào)度有兩種對(duì)齊調(diào)度方式,一種是左齊計(jì)劃,一種是右齊計(jì)劃。所謂擴(kuò)展的串行調(diào)度機(jī)制就是采用雙齊計(jì)劃進(jìn)行調(diào)度,實(shí)現(xiàn)過程分為:(1)采用串行調(diào)度方法生成一個(gè)左齊計(jì)劃;(2)在左齊計(jì)劃的基礎(chǔ)上,以左齊計(jì)劃的結(jié)束任務(wù)完工時(shí)間為基準(zhǔn),再生成右齊計(jì)劃;(3)若右齊計(jì)劃開始任務(wù)開始時(shí)間大于零,則整個(gè)右齊計(jì)劃同步左移至開始任務(wù)最早開始時(shí)間為零,即再進(jìn)行一個(gè)左齊計(jì)劃。通過這一調(diào)度機(jī)制就可以實(shí)現(xiàn)將食物源的解轉(zhuǎn)換為可行的調(diào)度方案。
2.2.4 算法的實(shí)現(xiàn)步驟
ABC算法求解RCPSP的實(shí)現(xiàn)步驟如下:
(1)初始化。ABC算法首先產(chǎn)生初始種群,種群數(shù)量為SN,也代表SN個(gè)解(食物源)。每一個(gè)解xi(i=1,2,…,SN)對(duì)應(yīng)了一組任務(wù)優(yōu)先權(quán)序列,通過擴(kuò)展的串行調(diào)度生成機(jī)制得到可行的調(diào)度方案,計(jì)算出每個(gè)xi的適應(yīng)值fiti。
(2)迭代過程。在初始化之后,進(jìn)入迭代(C=1,2,…,Cmax)過程,Cmax為最大迭代次數(shù)。在每次迭代中,三種類型的人工蜂執(zhí)行不同的操作,種群的全局最優(yōu)解就隨著人工蜂群每次迭代中所尋找的食物源適應(yīng)值的情況不斷更新。
①工作蜂有SN個(gè),對(duì)應(yīng)SN個(gè)食物源,工作蜂i的食物源為xi,工作蜂i在種群中隨機(jī)選擇一個(gè)工作蜂k做它的鄰居,并在工作蜂k的食物源xk的n維向量中隨機(jī)選擇一位d(d=1,2,…,n)。vi為工作蜂i的候選食物源,vi與xi除了第j位vid外,其余各位和xi一致。vid的計(jì)算方法為:

其中,fiti為工作蜂i的食物源的適應(yīng)值。跟隨蜂j通過輪盤賭的形式從工作蜂的食物源中選擇食物源,假設(shè)工作蜂i的食物源xi被選中,跟隨蜂j采用和①相同的方法來(lái)生產(chǎn)侯選食物源vi,同時(shí)采用和①相同貪婪策略在vi和xi之間進(jìn)行取舍,traili的設(shè)置方法亦同上。
③當(dāng)某一食物源xi的traili等于最大重復(fù)使用次數(shù)的限定值時(shí),偵查蜂就會(huì)隨機(jī)生成一個(gè)新的食物源取代xi,原來(lái)的食物源被舍棄不用。
(3)結(jié)束。當(dāng)步驟(2)完成Cmax次迭代后,ABC算法結(jié)束,輸出最優(yōu)調(diào)度方案及項(xiàng)目最短工期。
3 仿真實(shí)驗(yàn)
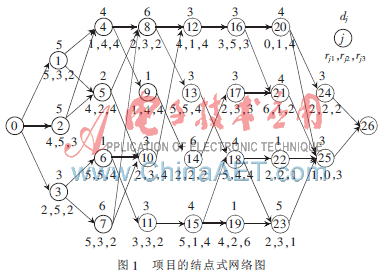
為了驗(yàn)證ABC算法求解RCPSP的有效性,本文選取的算例為項(xiàng)目的結(jié)點(diǎn)式網(wǎng)絡(luò)圖[6],如圖1所示,項(xiàng)目的任務(wù)集為J={0,1,2,…,25,26},任務(wù)0和26為虛任務(wù)。項(xiàng)目的可更新資源種類為三種,每種資源在單位時(shí)間內(nèi)大最大使用限額為6。圖1中,結(jié)點(diǎn)圓圈內(nèi)數(shù)字為任務(wù)編號(hào),結(jié)點(diǎn)上方數(shù)字為任務(wù)工期,結(jié)點(diǎn)下方數(shù)字分別為該任務(wù)對(duì)三種資源的使用量。
ABC仿真實(shí)驗(yàn)選取蜂群數(shù)量NP=20,即食物源SN=10,最大迭代次數(shù)Cmax=50,工作蜂生成候選食物源應(yīng)用式(5)時(shí),取參數(shù)ω1=0.7;跟隨蜂尋找候選食物源應(yīng)用(5)式時(shí),取參數(shù)ω2=1。圖2給出了ABC算法在迭代中得到的項(xiàng)目工期的收斂過程,項(xiàng)目的工期的最優(yōu)解為64天,所得的最優(yōu)結(jié)果與參考文獻(xiàn)[5]一致,同時(shí)與參考文獻(xiàn)[5]比較來(lái)看,由于采用了擴(kuò)展的串行調(diào)度生成機(jī)制,初始解離最優(yōu)解距離更近。

圖3給出了應(yīng)用ABC算法得到的本算例最優(yōu)調(diào)度時(shí)的甘特圖。圖4給出了此時(shí)項(xiàng)目可用資源的利用情況圖,由圖可見,在最短項(xiàng)目工期為64天的情況下,各任務(wù)在執(zhí)行過程中滿足三種資源的限制。

本文針對(duì)資源受限的項(xiàng)目調(diào)度優(yōu)化問題的數(shù)學(xué)模型,提出了一種基于優(yōu)先權(quán)編碼的人工蜂群算法,通過擴(kuò)展的串行調(diào)度生成機(jī)制將優(yōu)先權(quán)編碼轉(zhuǎn)換為可行的調(diào)度方案。實(shí)際算例仿真結(jié)果表明,人工蜂群算法能夠有效地求解資源受限的項(xiàng)目調(diào)度問題,算法的收斂速度較快,精度較高。既提高了算法的優(yōu)化效率,又提高了算法的優(yōu)化精度,同時(shí)擴(kuò)展調(diào)度機(jī)制與串行調(diào)度生成機(jī)制相比具有明顯的優(yōu)點(diǎn)。
參考文獻(xiàn)
[1] BLAZEWICZ J, LENSTRA J K, RINNOOY K A H G. Scheduling subject to resource constraints: classifcation and complexity[J]. Discrete Applied Mathematics. 1983,5 (1):11-24.
[2] KARABOGA D. An idea based on honey bee swarm for numerical optimization[R]. Technical Report-TRO6, 2005.
[3] KARABOGA D, BASTURK B. A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm[J]. Journal of Global Optimization, 2007,39(3): 459-471.
[4] KARABOGA D, BASTURK, B. On the performance of artificial bee colony(ABC) algorithm[J]. Applied Soft Computing. 2008,8(1):687-697.
[5] Deng Linyi, Lin Yan, Chen Ming. Hybrid ant colony optimization for the resource-constrained project scheduling problem[J]. Journal of Systems Engineering and Electronics 2010,21(1):67-71.
[6] Zhang Hong, Li Heng, TAM C M. Particle swarm optimization for resource-constrained project scheduling[J]. International Journal of Project Management 2006,24:83-92.

