摘  要： 介紹了基于遞推最小二乘法進行系統(tǒng)辨識的基本原理,，對給定的實際輸入輸出數(shù)據(jù)運用MATLAB的M語言編寫遞推最小二乘算法，最后給出相應的仿真結果和分析,，并對得到的模型進行驗證,。
關鍵詞： 系統(tǒng)辨識；遞推最小二乘,；MATLAB,；仿真

    對于一個系統(tǒng),，在輸入輸出數(shù)據(jù)的基礎上，從一組給定模型類中,，確定一個與所測系統(tǒng)等價的模型,，這種方法叫做辨識。辨識是在實際應用中獲取系統(tǒng)模型的最為重要的手段之一,，也是數(shù)學模型和實際應用聯(lián)系的紐帶,。而最小二乘類辨識則是在給定的結構框架下，利用模型輸出與實際輸出間的誤差不斷糾正模型參數(shù),，最終得到最優(yōu)模型的過程[1],。在使用最小二乘法進行參數(shù)估計時，為了實現(xiàn)實時控制,，必須優(yōu)化成遞推算法RLS（Recursive Least Square）,，主要用于在線辨識。MATLAB是一種面對科學計算,、可視化以及交互式程序設計的高科技計算環(huán)境,。它將數(shù)值分析、矩陣計算,、科學數(shù)據(jù)可視化以及非線性動態(tài)系統(tǒng)的建模和仿真等諸多強大功能集成在一個易于使用的視窗環(huán)境中,，為科學研究、工程設計以及必須進行有效數(shù)值計算的眾多科學領域提供了一種全面的解決方案,，并在很大程度上擺脫了傳統(tǒng)非交互式程序設計語言（如C,、Fortran）的編輯模式，代表了當今國際科學計算軟件的先進水平[2],。
    本文使用MATLAB2009a的M語言對遞推最小二乘算法進行編程,，最后使用MATLAB自帶的辨識工具箱SIT(System Identification Toolbox)對得到的仿真結果進行了驗證。
1 線性系統(tǒng)辨識[3]
1.1 問題描述

其對應的辨識問題的表達形式如圖2所示,。
    圖2中,，h(k)和z(k)是模型的輸入輸出變量，在離散點上必須是可觀測的,；v(k)為模型噪聲,；?茲是未知模型參數(shù)。

2 仿真實例[4]
2.1 選擇輸入信號
    為了準確辨識系統(tǒng)參數(shù),，對輸入信號有如下要求：在辨識時間內，過程的動態(tài)必須被輸入信號持續(xù)激勵,。從譜分析角度看,，這就意味著信號頻帶能覆蓋系統(tǒng)的頻帶寬度。除此之外還要求信號有可重復性,，不能是不可重復的隨機噪聲,，因此本文選擇滿足上述要求的M序列作為輸入信號,。
2.2 先驗知識
    在對給定的過程進行辨識之前，掌握如下先驗知識：純遲延d=0,；模型如式(7)所示,，且數(shù)據(jù)長度L=1 000，na=nb=4,。

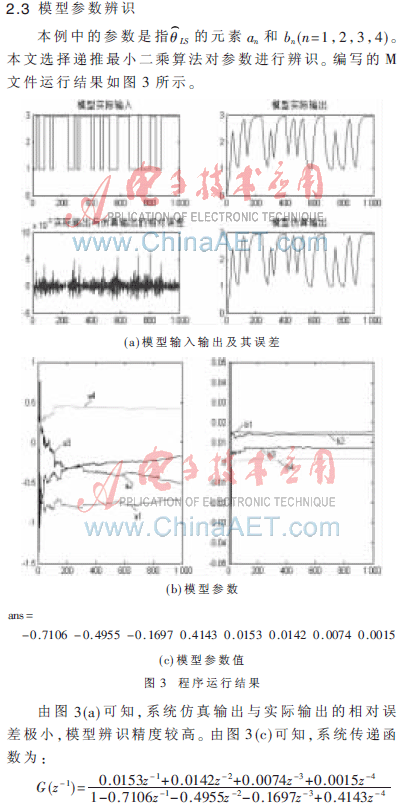
2.4 模型驗證
    本文使用MATLAB自帶的辨識工具箱SIT(System Identification Toolbox)對得到的仿真結果進行驗證,。在MATLAB2009a的Command Window中輸入ident命令，SIT被打開,。需將給定的輸入輸出數(shù)據(jù)設置為該模塊的輸入輸出方可進行驗證,。結果如圖4所示。

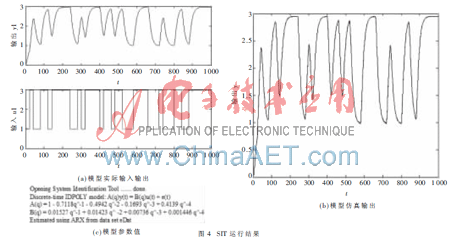
    由圖3(c)和圖4(c)中所得的模型參數(shù)可以看出,，本文編寫的遞推最小二乘算法可以快速準確地估計出系統(tǒng)參數(shù),，獲得較好的辨識結果。
    本文介紹了基于遞推最小二乘法進行系統(tǒng)辨識的基本原理,，對給定的實際輸入輸出數(shù)據(jù)運用MATLAB的M語言編寫遞推最小二乘算法,，最后給出相應的仿真結果和分析，并對得到的模型進行了驗證,。遞推最小二乘法的算法簡單,，能減少計算量，減少數(shù)據(jù)在計算機中占用的內存,，并實時辨識出系統(tǒng)動態(tài)特性以供實時控制和預報,。
參考文獻
[1] 倪博溢，蕭德云.MATLAB 環(huán)境下的系統(tǒng)辨識仿真工具箱[J].系統(tǒng)仿真學報,，2006,，18(6)：1493-1496.
[2] 石賢良，吳成富.基于MATLAB的最小二乘法參數(shù)辨識與仿真[J].微處理機,，2005,，26(6)：44-46.
[3] 方崇智，蕭德云.過程辨識[M].北京：清華大學出版社,，1988.
[4] 張志涌.精通MATLAB6.5版[M].北京：北京航空航天大學出版社,，2003.