可靠性和有效性是通信系統(tǒng)必須考慮的兩個(gè)主要因素,，無線通信還需要考慮頻譜效率和功率效率,，對(duì)于對(duì)抗性無線通信，還希望獲得更好的抗干擾性和低截獲性,。截獲最基本的前提是信號(hào)強(qiáng)度足夠,，也就是說,到達(dá)截獲系統(tǒng)天線處的信號(hào)必須要達(dá)到一定的功率密度，降低通信所需的發(fā)射功率能夠在同等條件下獲得更好的低截獲性,，同時(shí),，采用更低的發(fā)射功率完成通信對(duì)無線設(shè)備的能量損耗也具有重要意義。信道編碼能夠提高通信的可靠性,，在同樣的信噪比情況下,，獲得更低的誤碼率，也就是說,，在同樣條件下,，能夠采用更小的發(fā)射功率實(shí)現(xiàn)同樣的誤碼率，因此能夠具有更好的功率效率和低截獲性能,，但同時(shí)又因?yàn)樵黾恿诵畔⒌娜哂辔欢鵂奚艘欢ǖ念l譜利用率,。因此，需要在功率利用率和頻譜利用率之間尋找一個(gè)平衡,，先進(jìn)的編碼技術(shù)與高效的調(diào)制技術(shù)相結(jié)合能夠有效解決這一難題,。對(duì)于實(shí)際應(yīng)用而言，可實(shí)現(xiàn)性是一個(gè)更為重要的因素,，因此,，如何降低系統(tǒng)中所采用技術(shù)的算法復(fù)雜度來提高可實(shí)現(xiàn)性也是系統(tǒng)設(shè)計(jì)所要考慮的一個(gè)重要問題。本文從串行級(jí)聯(lián)編碼理論入手，綜合考慮系統(tǒng)的功率效率,、頻譜效率和可實(shí)現(xiàn)性,，在對(duì)LDPC和CPM編譯碼算法進(jìn)行簡(jiǎn)化的基礎(chǔ)上，提出了一種新的串行級(jí)聯(lián)編碼調(diào)制系統(tǒng)的設(shè)計(jì)方案,，并對(duì)該系統(tǒng)的性能進(jìn)行了仿真和對(duì)比分析,，最后，給出了具體實(shí)現(xiàn)時(shí)硬件資源的使用情況,。
1 CPM與LDPC簡(jiǎn)介
    連續(xù)相位調(diào)制(Continuous Phase Modulation)是一種包絡(luò)恒定,、相位連續(xù)的調(diào)制方式，具有較高的頻譜利用率和功率利用率,。這種調(diào)制最大的特點(diǎn)就是它的相位連續(xù),，從而降低了信號(hào)的頻譜旁瓣，使能量主要集中在主瓣中,，同時(shí)由于其相位具有記憶性,，使得該調(diào)制方式具有一定的編碼增益。恒包絡(luò)特性使得該調(diào)制方式對(duì)功放的非線性不敏感,，尤其適用于需要使用非線性功率放大器的無線通信系統(tǒng),，在遠(yuǎn)距離通信中有很大優(yōu)勢(shì)?；谠撜{(diào)制的無線通信系統(tǒng)早在20世紀(jì)90年代就已應(yīng)用于美國(guó)的軍方系統(tǒng),。
    低密度奇偶校驗(yàn)碼（Low Density Parity Check Code）是一種分組碼，它是一種性能優(yōu)良的信道編碼,，在中長(zhǎng)碼時(shí)有著優(yōu)于Turbo碼的性能,，能夠獲得距離香農(nóng)限零點(diǎn)幾分貝的良好性能，該碼的校驗(yàn)矩陣很稀疏,，因此譯碼復(fù)雜度比Turbo碼更低,，并且可以實(shí)現(xiàn)并行譯碼，減小譯碼時(shí)延,。目前已被廣泛應(yīng)用在通信,、廣播,、HDD硬盤等領(lǐng)域,。
    1966年FORNEY G D提出了一種串行級(jí)聯(lián)編碼方案[1]，級(jí)聯(lián)編碼是指可以對(duì)信息序列先進(jìn)行一種編碼(外碼),，然后再對(duì)外碼編碼所得序列進(jìn)行另一種編碼(內(nèi)碼),。Forney的研究表明級(jí)聯(lián)編碼能夠獲得較大性能改善，使譯碼錯(cuò)誤概率隨著碼長(zhǎng)呈指數(shù)減少,，而譯碼復(fù)雜度只是以代數(shù)形式增加,。
2 基于LDPC的CPM調(diào)制系統(tǒng)模型
　    根據(jù)Rimoldi的研究[2]，CPM可以分解為連續(xù)相位編碼器（Linear Continuous Phase Encoder）和無記憶調(diào)制器（Memoryless Modulator）兩部分,，其中CPE可以看做碼率為1的卷積碼,，因此可以作為內(nèi)碼與其他信道編碼的級(jí)聯(lián),。通常，在級(jí)聯(lián)編碼系統(tǒng)的外碼和內(nèi)碼之間加入一個(gè)交織器,，可以大大提高性能,。但是，由于LDPC本身的內(nèi)在交織性使得經(jīng)過編碼的LDPC碼已經(jīng)具有類似于交織器的打亂順序的特點(diǎn),，所以在LDPC與CPM級(jí)聯(lián)的系統(tǒng)中交織器不是必須的,。因此，本文提出了如圖1所示的基于LDPC編碼的CPM調(diào)制系統(tǒng)模型,。
    在發(fā)射端,，需要發(fā)送的信息字經(jīng)LDPC編碼后進(jìn)行符號(hào)映射，然后輸入到M進(jìn)制的CPM中,，CPE部分對(duì)輸入信息進(jìn)行連續(xù)相位編碼,，編碼后獲得的相位經(jīng)過MM調(diào)制器調(diào)制后發(fā)射出去。
　在接收端,，采用基于SISO算法的CPM譯碼器進(jìn)行硬判決并輸出符號(hào)的軟信息,。CPM軟譯碼器對(duì)每個(gè)時(shí)刻可能碼字符號(hào)的概率進(jìn)行比較判決，并將這個(gè)符號(hào)的概率作為似然概率輸出,，對(duì)LDPC譯碼器進(jìn)行初始化,。經(jīng)LDPC譯碼模塊進(jìn)行迭代譯碼后作硬判決輸出。
3 系統(tǒng)的工作過程
3.1 系統(tǒng)的編碼調(diào)制過程
　    鑒于LDPC碼編譯碼算法的復(fù)雜度較高,，直接使用將帶來較高的編譯碼時(shí)延,，會(huì)給工程實(shí)現(xiàn)增加難度。因此,在系統(tǒng)設(shè)計(jì)時(shí),采用了準(zhǔn)循環(huán)LDPC（Quasi Cyclic LDPC）碼[3],，該碼的準(zhǔn)循環(huán)特性使得該碼在編譯碼上具有規(guī)律性,，可采用簡(jiǎn)單的移位寄存器實(shí)現(xiàn)，能夠有效降低譯碼復(fù)雜度,。
　    QC-LDPC的編碼采用了RICHARDSON等人提出的“貪婪算法”[4],，該算法通過對(duì)行滿秩的校驗(yàn)矩陣H進(jìn)行行列置換，變換成近似下三角形式,，同時(shí)將H劃分為幾個(gè)小塊的稀疏矩陣,，然后再進(jìn)行編碼，對(duì)矩陣的行列置換保持了矩陣的稀疏性,，降低了編碼的復(fù)雜度,，實(shí)現(xiàn)了近似線性編碼，在實(shí)際工程中得到了較為廣泛的應(yīng)用,。

3.2 系統(tǒng)的解調(diào)譯碼過程
　參考文獻(xiàn)[6]設(shè)計(jì)的LDPC+CPM串行級(jí)聯(lián)系統(tǒng)采用了兩譯碼器之間信息互相傳遞并進(jìn)行迭代,，直到LDPC碼譯碼器譯碼成功或者達(dá)到最大迭代次數(shù)后判決輸出。這種設(shè)計(jì)基于LDPC與CPM兩種譯碼算法之間相互迭代和傳遞消息，雖然較本文的系統(tǒng)結(jié)構(gòu)會(huì)有一定的性能優(yōu)勢(shì),，但卻極大地增加了譯碼復(fù)雜度,，帶來了惡劣的處理延時(shí)和存儲(chǔ)空間問題，實(shí)際應(yīng)用中硬件實(shí)現(xiàn)困難,。因此經(jīng)仿真分析并權(quán)衡性能和可實(shí)現(xiàn)性后提出了圖1所示的系統(tǒng)結(jié)構(gòu),，這樣的結(jié)構(gòu)不需要在LDPC和CPM兩者之間進(jìn)行迭代譯碼，使得系統(tǒng)能夠獲得更快的譯碼速度和更少的數(shù)據(jù)存儲(chǔ),。
　 如圖1所示,，CPM調(diào)制后的信號(hào)經(jīng)過信道后，在接收端同本地存儲(chǔ)的所有發(fā)射基帶波形進(jìn)行匹配相關(guān),并將相關(guān)值作為似然信息送入CPM的SISO譯碼器進(jìn)行一次迭代更新,。CPM譯碼迭代采用的是基于BCJR算法的SISO譯碼方法[7],，輸出更新后的模板匹配最大值。通過此最大值,，可以確定其所對(duì)應(yīng)的C,，而所存模板中每一個(gè)C對(duì)應(yīng)的“當(dāng)前時(shí)刻”的輸入信息符號(hào)un是確定的。由此,，經(jīng)匹配相關(guān)可確定un,。再將un分解為原信息比特，并通過相關(guān)峰值獲取每一信息比特的初始消息,，傳遞給QC-LDPC譯碼器進(jìn)行譯碼迭代,。

　由于置信傳播（Belief-propagation）算法在橫向迭代過程中需要大量的乘法運(yùn)算，復(fù)雜度較高,。因此,，系統(tǒng)中的QC-LDPC譯碼采用了歸一化的最小和譯碼算法（Normalized Min-Sum Decoding Algorithm）[8]，該算法在橫向迭代過程中,，采用近似算法,，將橫向迭代簡(jiǎn)化為數(shù)值比較過程，即將非線性關(guān)系變換為線性關(guān)系,，從而減小了譯碼復(fù)雜度,，同時(shí)通過調(diào)整比例系數(shù)，在非線性關(guān)系變換為線性關(guān)系的過程中增加BP算法和MSA兩種算法間的運(yùn)算擬合度,，從而降低誤差,。經(jīng)LDPC譯碼后判決并輸出譯碼后的信息。
4 性能仿真與分析
    為檢驗(yàn)所設(shè)計(jì)系統(tǒng)的性能,，對(duì)不同級(jí)聯(lián)方式系統(tǒng)的誤碼性能進(jìn)行了Matlab仿真,。仿真中采用加性高斯白噪聲(AWGN) 信道模型,。各方案的具體參數(shù)見表1,。

    其中，LDPC碼選用CCSDS提供的碼率R=2/3，信息位k=1 024的QC-LDPC碼,，SCCPM系統(tǒng)中CC(3,[5,7])編碼交織長(zhǎng)度為1 024,，單個(gè)符號(hào)采樣點(diǎn)相同fs=11。仿真結(jié)果如圖2和圖3所示,。

    由圖2可以看出,，在同樣CPM調(diào)制參數(shù)下，本文設(shè)計(jì)的LDPC+CPM系統(tǒng)誤碼性能要優(yōu)于SCCPM系統(tǒng),。SCCPM的錯(cuò)誤平層現(xiàn)象[9]在圖2中有所體現(xiàn),，因?yàn)镾CCPM譯碼器采用類似于Turbo碼的迭代譯碼從而獲得非常好的誤碼性能，但是又由于其外碼為自由距離非常小的卷積碼,，使得大約在10e-6時(shí)誤比特率隨著信噪比增加開始緩降,。而LDPC具有瀑布區(qū)，在EbN0=1.5~2.5 dB之間誤碼性能隨信噪比增加急劇提升,。
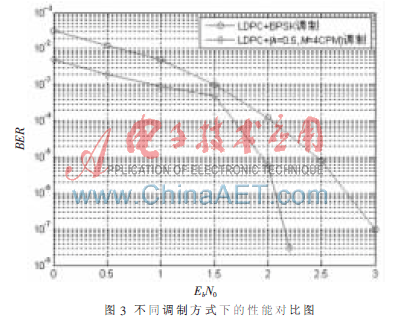
   由圖3可以看出,，在同樣的編碼下，LDPC+CPM系統(tǒng)的性能要優(yōu)于LDPC+BPSK系統(tǒng),。LDPC+BPSK系統(tǒng)中,，首先經(jīng)過BPSK解調(diào)將其作為L(zhǎng)DPC譯碼的初始似然信息，然后LDPC譯碼器進(jìn)行迭代譯碼,。LDPC+CPM系統(tǒng)中,，首先進(jìn)行CPM的解調(diào)譯碼，這相當(dāng)于G.D.Forney模型中的內(nèi)碼譯碼,，然后將譯碼軟信息傳遞到LDPC譯碼器中進(jìn)行第二級(jí)譯碼,，顯然級(jí)聯(lián)碼系統(tǒng)具有更好的性能。如圖所示,，LDPC+CPM較LDPC+BPSK方式在10e-6的誤碼層面上需要的信噪比大約減少0.7 dB,，相當(dāng)于CPM調(diào)制提供了約0.7 dB的編碼增益，這一結(jié)果與FORNEY G D的研究理論也是相符合的,。

5 硬件實(shí)現(xiàn)情況
　系統(tǒng)的實(shí)現(xiàn)采用了DSP+FPGA架構(gòu),，其中DSP主要負(fù)責(zé)完成系統(tǒng)數(shù)據(jù)流的控制，F(xiàn)PGA負(fù)責(zé)完成QC-LPDC碼的編譯碼算法及CPM調(diào)制的調(diào)制解調(diào),模板匹配所用模板的存儲(chǔ)等[10],。
    FPGA芯片選用的XILINX公司VIRTEX-5系列的XC5VSX95T,。經(jīng)ISE軟件編程仿真通過后，得到的FPGA芯片資源使用報(bào)告如圖4所示,。

    可以看到,，乘法器資源占用率只有23%，這表明文中對(duì)系統(tǒng)結(jié)構(gòu)的優(yōu)化設(shè)計(jì)及主要算法的近似簡(jiǎn)化能夠有效減少編譯碼時(shí)的運(yùn)算量,，降低了對(duì)硬件資源的需求,。
　CPM是一種具有很多優(yōu)點(diǎn)的先進(jìn)調(diào)制技術(shù),，其優(yōu)秀的功率譜性能以及恒包絡(luò)特點(diǎn)使得該調(diào)制技術(shù)非常適用于遠(yuǎn)距離無線通信，相對(duì)于其他級(jí)聯(lián)方式的系統(tǒng)設(shè)計(jì),，基于LDPC的CPM調(diào)制系統(tǒng)能夠采用更小的發(fā)射功率來完成同等距離上的無線通信,，這對(duì)于對(duì)抗性無線通信的低截獲性需求具有非常重大的意義。從可實(shí)現(xiàn)性角度出發(fā),對(duì)編碼和調(diào)制的編譯碼算法進(jìn)行簡(jiǎn)化,，減少乘法運(yùn)算,將非線性運(yùn)算通過合理近似轉(zhuǎn)換為線性運(yùn)算,，從而降低各算法的實(shí)現(xiàn)復(fù)雜度。通過分析比較,，優(yōu)化系統(tǒng)結(jié)構(gòu),取消LDPC編碼和CPM調(diào)制之間的迭代運(yùn)算,，以犧牲較小的性能為代價(jià)，換得更小的譯碼延時(shí)和更少的資源需求,，降低系統(tǒng)的實(shí)現(xiàn)復(fù)雜度,，使得整個(gè)系統(tǒng)能夠在一片F(xiàn)PGA中得以實(shí)現(xiàn)，這對(duì)于現(xiàn)實(shí)應(yīng)用具有重要的參考價(jià)值和指導(dǎo)意義,。
參考文獻(xiàn)
[1] FORNEY G D, Jr. Concatenated Codes[M]. M.I.T.Press, Cambridge, MA, USA, 1966.
[2] RIMOLDI B E, A decomposition approach to CPM[J].IEEE Trans. Inf. Theory, 1988,34(2):260-270.
[3] FOSSORIER M P. Quasi-cyclic low-density parity-check codes from circulant permutation matrices [J]. IEEE Transactions on Informatron Theory, 2004(50):1788-1793.
[4] RICHARDSON T J, URBANKE R. L. Efficient encoding of  low-density parity-check codes[J]. IEEE Transactions on  IT, 2001,47(2):638-656.
[5] AULIN T, SUNDBERG C E W. Continuous phase modulation Part I[J]．IEEE Trans. Comm, 1981(29):196-225.
[6] 薛睿,趙旦峰,肖春麗.基于Turbo迭代算法的LDPCC-CPM系統(tǒng)接收機(jī)設(shè)計(jì)[J].深圳大學(xué)學(xué)報(bào)（理工版）, 2010,27(3):301-305.
[7] PAPAHARALABOS S, SYBIS M, TYCZKA et al. Modified Log-Map algorithms for simplified decoding of turbo and turbo TCM codes[J]. VETECS., 2009,69(3):1-5.
[8] Chen Jinghu, DHOLAKIA A, Hu Xiaoyu, et al. Reduced complexity decoding of ldpc codes [J]. IEEE Trans. on Commun., 2005,53(8):1288-1298.
[9] 張敏,黃俊偉,孟杰.CMMB中LDPC碼的編譯碼研究及仿真性能分析[J].電子技術(shù)應(yīng)用,2009,35(9):112-115.
[10] 賈哲,鄭翔.一種四進(jìn)制CPM調(diào)制器的設(shè)計(jì)與FPGA實(shí)現(xiàn)[J].電訊技術(shù),2006,46(5)：153-155.