《電子技術(shù)應(yīng)用》
您所在的位置：首頁 > 通信與網(wǎng)絡(luò) > 設(shè)計應(yīng)用 > LDPC碼節(jié)點剩余度置信傳播譯碼改進
LDPC碼節(jié)點剩余度置信傳播譯碼改進
2017年電子技術(shù)應(yīng)用第11期
周 華1,，2，3,，翁少輝1,，3，馮 姣1,，3
1.南京信息工程大學(xué),，江蘇 南京210044；2.江蘇省大氣環(huán)境與裝備技術(shù)協(xié)同創(chuàng)新中心,，江蘇 南京210044,； 3.江蘇省氣象探測與信息處理重點實驗室，江蘇 南京210044
摘要： 低密度奇偶校驗（LDPC）碼的剩余度置信傳播（RBP）和基于校驗節(jié)點的剩余度置信傳播（NWRBP）譯碼算法是根據(jù)剩余度值的有序度量,，動態(tài)選擇最大剩余度值所在的邊或校驗節(jié)點,，對其依次進行更新。對比依次同步更新所有校驗節(jié)點和變量節(jié)點的flooding算法,，NWRBP算法的收斂速度和譯碼性能有了很大的提高,。基于NWRBP算法,，提出一種改進型NWRBP（ENWRBP）算法,，即統(tǒng)計NWRBP譯碼過程中各變量節(jié)點的更新次數(shù)。如果NWRBP迭代譯碼失敗,，則將更新次數(shù)最少的變量節(jié)點的初始化值設(shè)置為0,，重新譯碼,。仿真結(jié)果表明，與NWRBP相比,，ENWRBP譯碼算法降低了誤碼率和誤幀率,。
中圖分類號： TN92
文獻標(biāo)識碼： A
DOI：10.16157/j.issn.0258-7998.170678
中文引用格式： 周華，翁少輝,，馮姣. LDPC碼節(jié)點剩余度置信傳播譯碼改進[J].電子技術(shù)應(yīng)用,，2017，43(11)：107-111.
英文引用格式： Zhou Hua,，Weng Shaohui,，F(xiàn)eng Jiao. Enhanced node-wise residual belief propagation for LDPC codes[J].Applica-
tion of Electronic Technique，2017,，43(11)：107-111.
Enhanced node-wise residual belief propagation for LDPC codes
Zhou Hua1,，2，3,，Weng Shaohui1,，3，F(xiàn)eng Jiao1,，3
1.Nanjing University of Information Science and Technology,，Nanjing 210044，China,； 2.Jiangsu Collaborative Innovation Center on Atmospheric Environment and Equipment Technology,，Nanjing 210044，China,； 3.Jiangsu Key Laboratory of Meteorological Observation and Information Processing,，Nanjing 210044，China
Abstract： Residual belief-propagation(RBP) and Node-wise residual belief-propagation(NWRBP) decoding algorithm based on low-density parity-check(LDPC) codes dynamically select the edge or check node where the maximum residual value is located to update, according to the order of the residual metric. Compared with the flooding algorithm of which simultaneously update all the check nodes and variable nodes in turn, the convergence speed and decoding performance of NWRBP algorithm have been greatly improved. Based on NWRBP algorithm, this paper presents an enhanced NWRBP（ENWRBP）algorithm, which counts the number of updates for each variable node during the NWRBP decoding process. If the decoding fails, it will set the initialized LLR value of the variable node with the least number of updates to zero and restart the decoding. Simulation results show that compared with NWRBP, ENWRBP improves the decoding performance with lower the bit error rate and frame error rate.
Key words : low density parity check code,；belief-propagation,；residual degree；iterative decoding

0 引言

    碼率為R=(N-M)/N的低密度奇偶校驗(Low-Density Parity-Check,，LDPC)碼是一種線性分組碼[1-2],。LDPC碼因其優(yōu)異的譯碼性能，已經(jīng)受到了越來越多的關(guān)注,，并且日前在深空通信,、光纖通信、衛(wèi)星數(shù)字視頻,、音頻廣播等領(lǐng)域已經(jīng)得到了廣泛的應(yīng)用[3],。

    LDPC碼的傳統(tǒng)迭代譯碼算法flooding[4-6]，又稱為兩相的消息傳遞,，是最簡單的譯碼方式,。flooding算法這種在一次迭代中順序更新所有節(jié)點的方式，導(dǎo)致其譯碼的收斂速度較慢,，并且需要大量的迭代次數(shù)才能達到想要的譯碼效果,。為了減少迭代的次數(shù)和收斂速度, 時序置信傳播譯碼算法[7-8]（Belief-Propagation，BP）被提出,。在時序譯碼算法中,，假設(shè)校驗節(jié)點被分成p個子集，在一次迭代過程中,，第一個子集中從變量節(jié)點到校驗節(jié)點的信息被更新,，然后從校驗節(jié)點到相鄰的變量節(jié)點的信息要被更新并傳播，同樣其他p-1個校驗節(jié)點的子集也同時相應(yīng)地被更新,。很明顯,，一次迭代過程也涉及到所有變量節(jié)點以及所有的校驗節(jié)點的子集，因此,，每次譯碼迭代,，時序譯碼算法的計算復(fù)雜度和傳統(tǒng)flooding相同，但是其收斂速度對比flooding算法,，要快過兩倍,。盡管置信傳播算法有很好的譯碼性能，但為了進一步提高譯碼性能,，其不是最好的選擇,，最終，Casado等人將剩余度概念運用到了置信傳播[9-10],，并提出了兩種時序算法：基于剩余度置信(Residual Belief Propagation,，RBP)傳播譯碼算法、基于校驗節(jié)點的剩余度置信傳播(Node-Wise RBP,，NWRBP)譯碼算法[11-12],。

    RBP算法和NWRBP算法這種迭代機制會導(dǎo)致有的變量節(jié)點很少有機會去將它們本身的消息傳播到整個譯碼過程中，所以,，其譯碼算法不會達到最好的譯碼效果,。為了減少這種情況帶來的誤差，本文提出了一種改進型NWRBP(Enhanced NWRBP,，ENWRBP)算法,，在迭代譯碼過程中，如果NWRBP算法譯碼沒有成功,，則依次將更新最少次數(shù)的變量節(jié)點的初始化對比似然數(shù)值(Log-Likelihood Radio,，LLR)設(shè)置為0，并重新譯碼,，直到譯碼正確或達到最大測試次數(shù),。本算法最多測試T個變量節(jié)點,。該算法改變了校驗節(jié)點的更新順序，均衡了變量節(jié)點的更新次數(shù),，從而提高了LDPC碼的譯碼性能,。

1 LDPC碼的RBP和NWRBP譯碼算法

    對于規(guī)則(N，J,，K)LDPC碼,，N表示碼長，J和K分別表示校驗矩陣H行和列的重量,。LDPC碼可以用Tanner圖表示,。Tanner圖由變量節(jié)點、校驗節(jié)點以及連接變量節(jié)點和校驗節(jié)點的邊組成,。變量節(jié)點ci對應(yīng)矩陣H中的第i列,，校驗節(jié)點vj對應(yīng)矩陣H中的第j行。如果hij=1,，表明Tanner圖中節(jié)點vj和ci由一條邊相連,，否則不相連。圖1所示為規(guī)則(6,，2,，3)LDPC碼的Tanner圖，校驗節(jié)點和變量節(jié)點分別用方框和圓表示,。每個節(jié)點連接的邊的個數(shù)稱之為該節(jié)點的度,，圖1所示LDPC碼的校驗節(jié)點和變量節(jié)點的度分別為3和2[13]。

tx6-t1.gif

tx6-gs1.gif

其中,，ni是服從均值為0,、方差為δ2的高斯白噪聲(表示為ni～N(0，δ2)),，且它們之間相互獨立,。Eb/No表示信噪比(Signal-to-Noise Ratio，SNR),，Eb表示發(fā)送前每個信息比特的能量,，No表示發(fā)送前噪聲功率譜密度以及δ2=No/2。在開始進行譯碼前,，對于通過一個BPSK AWGN信道的碼字,，最終接收序列的每個碼字的先驗概率的對數(shù)似然比(LLR)初始化為：

tx6-gs2-4.gif

    式(3)和式(4)描述了譯碼過程中LDPC碼變量節(jié)點和校驗節(jié)點之間的消息更新和傳遞規(guī)律。RBP和NWRBP算法是將剩余度值作為度量去調(diào)整更新順序的兩種主要算法機制,。剩余度是消息更新之前和之后差值的絕對值,。在LDPC譯碼中，剩余度值的定義值為：  

tx6-gs5.gif

    作為RBP的擴展和延伸,，RBP算法和NWRBP算法兩者的區(qū)別是：RBP動態(tài)選擇最大剩余度所在的邊進行更新,，而NWRBP動態(tài)選擇最大剩余度所在的校驗節(jié)點進行更新,。NWRBP詳細(xì)步驟見算法1。

    算法1：LDPC碼的NWRBP算法譯碼流程

tx6-sf1.gif

2 ENWRBP算法機制描述

    由于RBP譯碼算法和NWRBP譯碼算法每次通過一條邊或是一個校驗節(jié)點去更新傳播消息,，這樣會形成一個個相對獨立彼此沒有影響的子集合,，經(jīng)過數(shù)次迭代后,，可能就會導(dǎo)致忽略掉已經(jīng)被正確修改的錯誤比特節(jié)點,，再一次出現(xiàn)錯誤，所以,，RBP算法和NWRBP算法都具有一定的貪婪性,。而NWRBP譯碼算法根據(jù)節(jié)點更新消息，每個子集合范圍較大,，其貪婪性相對較弱,。因此，經(jīng)過大量的迭代譯碼后,，NWRBP算法的譯碼性能會優(yōu)于RBP算法譯碼性能,。然而，這兩種算法的性能受限于陷井集(trapping sets)的影響,，導(dǎo)致一些錯誤的變量節(jié)點(即誤碼)在迭代多次后很難被發(fā)現(xiàn),。經(jīng)研究發(fā)現(xiàn)，NWRBP在譯碼過程中,，節(jié)點更新的次數(shù)并不均衡,，存在某些節(jié)點更新次數(shù)少的現(xiàn)象，而相對于更新次數(shù)較多的變量節(jié)點,，更新次數(shù)較少的變量節(jié)點不能為相鄰節(jié)點提供足夠的有用信息,，亦或該節(jié)點無法從相鄰節(jié)點獲得有用信息，導(dǎo)致相鄰節(jié)點或其本身發(fā)生錯誤的概率更大,。本文正是利用此思想來減少帶來的誤差,，在NWRBP譯碼算法的基礎(chǔ)上提出一種改進算法Enhanced NWRBP(ENWRBP)。在NWRBP譯碼算法的一次譯碼過程中,，如果達到最大的迭代次數(shù)仍然不滿足譯碼成功條件,，那么就尋找到在迭代過程中更新最少次數(shù)的變量節(jié)點vmin，并且將最初經(jīng)高斯白噪聲信道接收到的序列對應(yīng)的初始對數(shù)似然數(shù)rmin設(shè)置為0,。隨后,，重新用NWRBP進行譯碼，直到譯碼成功或連續(xù)重復(fù)T上述過程,，即更新T次最少的變量節(jié)點,。ENWRBP算法過程描述如圖2，詳細(xì)步驟見算法2,。

tx6-t2.gif

    算法2：LDPC碼的ENWRBP算法譯碼流程

tx6-sf2.gif

tx6-sf2-x1.gif

3 仿真結(jié)果與討論

    本文中所有的仿真都是在二進制輸入加性高斯白噪聲(BI-AWGN)信道進行的,。譯碼方式采用基于剩余度置信傳播(RBP)算法,、基于校驗節(jié)點的剩余度置信傳播(NWRBP)算法,以及本文提出的基于校驗節(jié)點的改進剩余度置信傳播(ENERBP)算法，最大迭代次數(shù)設(shè)為100,，調(diào)制方式為BPSK,，具體的仿真結(jié)果如圖3~圖6所示。

tx6-t3.gif

tx6-t4.gif

tx6-t5.gif

tx6-t6.gif

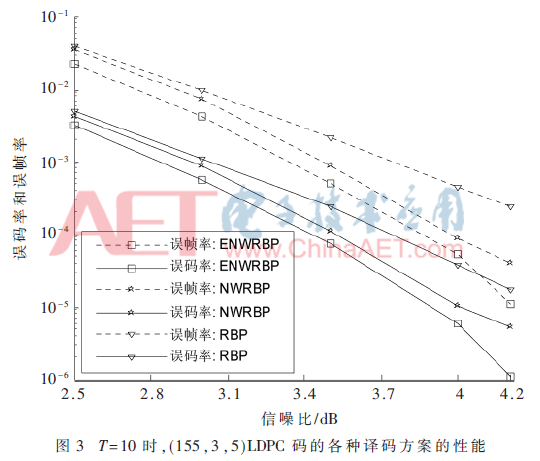
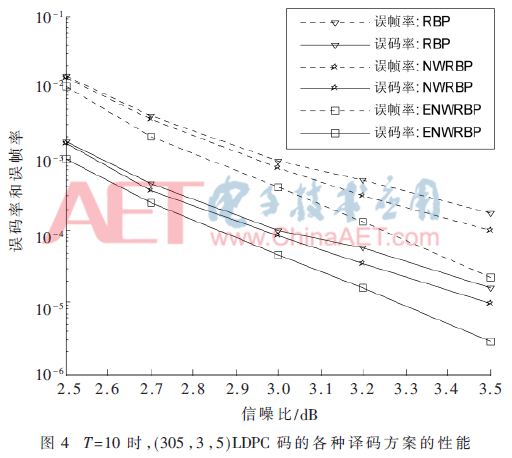
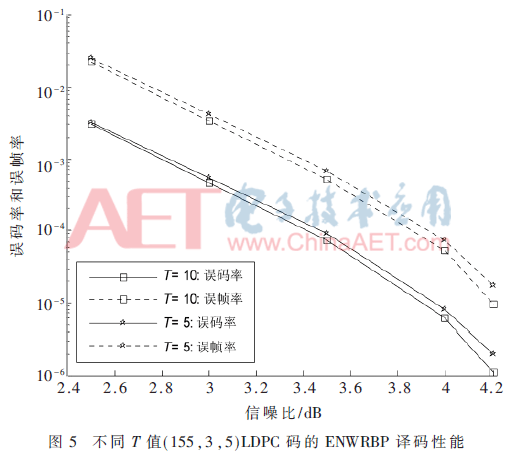
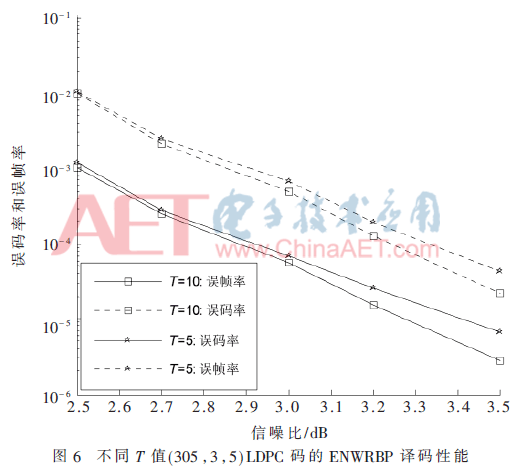
    圖3和圖4中T=10時,，可以觀察到ENWRBP算法的譯碼性能要好于NWRBP和RBP算法,。在SNR值較低時，圖3中SNR值為2.5～3 dB,，圖4中為2.5～2.7 dB,，誤碼率BER和誤幀率FER的曲線三者大致相同。隨著SNR值的增加,，ENWRBP算法和NWRBP算法的譯碼曲線逐漸優(yōu)于RBP算法,，圖3中NWRBP算法和ENWRBP算法依然大致相同，直到SNR值為4.0 dB時,，ENWRBP算法開始優(yōu)于NWRBP算法,，圖4中ENWRBP算法在所示SNR范圍內(nèi)始終優(yōu)于RBP算法和NWRBP算法，并且這種優(yōu)勢隨著SNR值增大而逐漸擴大,。例如：如圖4所示,，在FER=2×10-4時，相比RBP和NWRBP,，ENWRBP的FER分別得到0.3 dB和0.18 dB的譯碼增益,；同樣，在BER=2×10-5時,，相比RBP和NWRBP,，ENWRBP的BER分別得到0.28 dB和0.16 dB的譯碼增益。

    通過圖5和圖6 ENWRBP譯碼性能的比較,，可以觀察到,，T=10時的曲線要低于T=5時的曲線，并且這種趨勢隨著SNR值的增大而增大,。例如：如圖6所示,，在FER=1×10-4時，相比T=5,，T=10得到0.8 dB的譯碼增益,；同樣，在BER=1×10-5時,，相比T=5,，T=10得到1.2 dB的譯碼增益。由此可見，通過增大變量節(jié)點初始LLR值置0嘗試次數(shù),，可進一步提高ENWRBP譯碼性能,。

4 結(jié)論

    本文在NWRBP算法的基礎(chǔ)上介紹了一種增強譯碼算法ENWRBP(Enhanced NWRBP)。相比較NWRBP算法,，該算法的譯碼性能優(yōu)于NWRBP,，特別是SNR值稍大時尤為明顯。仿真表明,，NWRBP在每次迭代過程中,，更新次數(shù)少的變量節(jié)點，其本身或相鄰節(jié)點發(fā)生誤碼的概率高于其他的變量節(jié)點,。ENWRBP譯碼算法針對這一點,，多次找到更新次數(shù)最少的變量節(jié)點，然后對該節(jié)點的初始化值置0,，并重新譯碼，從而提高了NWRBP算法譯碼性能,。另外,，本文提出的基于節(jié)點更新次數(shù)最小、置零初始化值的思路也可以運用于其他LDPC譯碼算法中,。

參考文獻

[1] Li Hua,，Zheng Linhua.Efficient puncturing scheme for irregular LDPC codes based on serial schedules[J].IEEE Communications Letters，2015,，19(9)：1508-1511.

[2] 白寶明,，孫成，陳佩瑤,，等.信道編碼技術(shù)新進展[J].無線電通信技術(shù),，2016，42(6)：1-8.

[3] MACKAY D J C,，NEAL R.Near Shannon limit performance of low density parity check codes[J].IEEE Electronics Letters,，1998，33(6)：457-458.

[4] 鄭偉,，馬曉越,，趙成晨.一種改進的LDPC碼BP譯碼算法[J].河北大學(xué)學(xué)報(自然科學(xué)版)，2016,，36(5)：547-553.

[5] 張福星,，許生旺.一種改進的多元LDPC碼譯碼算法[J].無線通訊技術(shù)，2016,，42(6)：56-81.

[6] GOLOV O,，AMRANI O.Edge-based scheduled BP in LDPC codes[C].IEEE International Symposium on Information Theory，2007：2376-2380.

[7] SAEJOON K，KARAM K.Two-staged informed dynamic scheduling for sequential belief propagation decoding of LDPC codes[J].IEEE Communication Letters,，2009,，13(3)：193-195.

[8] LEE H C，UENG Y L,，YEH S M,，et al.Two informed dynamic scheduling strategies for iterative LDPC decoders[J].IEEE Transactions on Communications，2013,，61(3)：886-896.

[9] CASADO A I V,，GRIOT M，WESEL R D.LDPC decoders with informed dynamic scheduling[J].IEEE Transactions on Communications,，2010,，58(12)：3470-3479.

[10] Song Lingyan，Hou Shujuan.Improved decoding of LDPC codes by variable-to-check residual belief propagation[C].International Conference on Communications & Networking in China,，2015：163-166.

[11] Liu Xingcheng,，Zhang Yuanbin，Cui Ru.Variable-node-based dynamic scheduling strategy for belief-propagation decoding of LDPC codes[J].IEEE Communications Letters,，2015,，19(2)：147-150.

[12] Han Guojun，Liu Xingcheng.An efficient dynamic schedule for layered belief-propagation decoding of LDPC codes[J].IEEE Communications Letters,，2009,，13(13)：193-195.

[13] KSCHISCHANG F R，F(xiàn)REY B J,，LOELIGER H A.Factor graphs and the sum-product algorithm[J].IEEE Transactions on Information Theory,，2001，47(2)：498-519.



作者信息：

周  華1,，2,，3，翁少輝1,，3,，馮  姣1，3

(1.南京信息工程大學(xué),，江蘇 南京210044,；2.江蘇省大氣環(huán)境與裝備技術(shù)協(xié)同創(chuàng)新中心，江蘇 南京210044,；

3.江蘇省氣象探測與信息處理重點實驗室,，江蘇 南京210044)

此內(nèi)容為AET網(wǎng)站原創(chuàng)，未經(jīng)授權(quán)禁止轉(zhuǎn)載,。