《電子技術(shù)應(yīng)用》
您所在的位置：首頁(yè) > EDA與制造 > 設(shè)計(jì)應(yīng)用 > 大型直線稀疏陣列的迭代FFT算法優(yōu)化
大型直線稀疏陣列的迭代FFT算法優(yōu)化
來(lái)源：電子技術(shù)應(yīng)用2012年第1期
黃 偉1,， 吳宏剛2,， 陳客松1
1. 電子科技大學(xué) 電子工程學(xué)院,， 四川 成都 610054; 2. 中國(guó)民用航空局第二研究所 科研開發(fā)中心,， 四川 成都 610041
摘要： 提出了一種基于迭代FFT算法的大型直線稀疏陣列（可放置陣元的柵格數(shù)為1 000）的旁瓣電平優(yōu)化方法，并給出了詳細(xì)的優(yōu)化步驟,。在給定的旁瓣約束條件下,，利用陣列因子與陣元激勵(lì)之間存在的傅里葉變換關(guān)系，對(duì)不同的初始隨機(jī)陣元激勵(lì)分別進(jìn)行迭代循環(huán)來(lái)降低稀疏陣列的旁瓣電平,。在迭代過程中,，根據(jù)稀疏率將陣元激勵(lì)按幅度大小置1置0來(lái)完成陣列稀疏。仿真實(shí)驗(yàn)證明了該方法的高效性和穩(wěn)健性,。
中圖分類號(hào): TN 820.1+5
文獻(xiàn)標(biāo)識(shí)碼: A
文章編號(hào)： 0258-7998(2012)01-0100-03
Large linear arrays thinning using iterative FFT algorithm
Huang Wei1, Wu Honggang2, Chen Kesong1
1. School of Electronic Engineering, UESTC, Chengdu 610054，China; 2. Research and Development Center, The 2nd Research Institute, Civil Aviation Administration, Chengdu 610041, China
Abstract： A method based on iterative FFT algorithm for large thinned linear arrays (1 000 element positions) featuring an optimal peak side-lobe level is presented and the detailed steps of the method are discussed. The side-lobe level can be reduced when each iteration loop meeting the given peak side-lobe requirement starts with a different random initialization of element excitations by using the Fourier transform relationship exists between the array factor and the element excitations. Array thinning is accomplished by setting the amplitudes of the largest element excitations to unity and the others to zero during each iteration cycle. Finally,，the simulated results confirming the great efficiency and the robustness of the new method are shown in this paper.
Key words : array antennas; large arrays; fast Fourier transform (FFT); iteration; side-control

    在許多實(shí)際工程應(yīng)用中,，只要求天線陣列有窄的掃描波束，而不要求有相應(yīng)的增益。如高頻地面雷達(dá)天線,、抗環(huán)境干擾的衛(wèi)星接收天線和射電天文中的干涉陣列等,。采用稀疏陣列（即從規(guī)則的柵格中抽去天線單元或接匹配負(fù)載）的方法可以構(gòu)造出一個(gè)降低了增益的高方向性天線陣列，以較少天線單元數(shù)達(dá)到掃描波束變窄的技術(shù)指標(biāo),，從而大大降低生產(chǎn)成本[1],。陣列的周期性變稀會(huì)使陣列方向圖出現(xiàn)非常高的旁瓣，稀疏陣列優(yōu)化設(shè)計(jì)的主要目的就是實(shí)現(xiàn)旁瓣性能最優(yōu)化,，即盡可能地降低峰值旁瓣電平（PSL）,。

    近年來(lái)，隨著計(jì)算機(jī)技術(shù)的飛速發(fā)展,，高效的稀疏陣列優(yōu)化方法已成為研究熱點(diǎn),。用于稀疏陣列優(yōu)化的算法主要有遺傳算法、模擬退火算法,、分區(qū)動(dòng)態(tài)規(guī)劃法,、粒子群算法以及最近出現(xiàn)的蟻群算法等。這些算法從本質(zhì)上來(lái)說(shuō)都是基于隨機(jī)性的自然算法,，在陣列大?。纯煞胖藐囋臇鸥駭?shù)）超過200的稀疏陣列的優(yōu)化設(shè)計(jì)當(dāng)中一般并不適用 [2]，而關(guān)于大型直線稀疏陣列（陣列大小大于500）的優(yōu)化問題,，國(guó)內(nèi)外鮮有研究,。
    本文介紹的基于迭代FFT算法的大型直線稀疏陣列的優(yōu)化方法是一種全新高效的優(yōu)化方法，只需要很少的計(jì)算時(shí)間就能得到顯著的優(yōu)化效果,。

2 迭代FFT算法
    運(yùn)用迭代FFT算法來(lái)實(shí)現(xiàn)大型直線稀疏陣列優(yōu)化的詳細(xì)步驟為[4]：
    (1) 參數(shù)初始化,，給定迭代循環(huán)總次數(shù)Num，陣列大小M,，稀疏率f,，旁瓣約束條件等參數(shù)。
    (2) 隨機(jī)產(chǎn)生一個(gè)初始陣元激勵(lì)數(shù)組Am,。數(shù)組大小為M,，有陣元的位置設(shè)置為1，無(wú)陣元的位置設(shè)置為0,。陣元數(shù)目T=f×M,。
    (3) 對(duì)Am作K（K>M）點(diǎn)的逆FFT變換，得到陣列因子AF,。
    (4) 找出AF中的旁瓣區(qū)域,，將旁瓣區(qū)域中不滿足給定的旁瓣約束的采樣值進(jìn)行處理，變成旁瓣約束允許的最大旁瓣電平值,。
    (5) 對(duì)處理后的AF作K點(diǎn)的FFT變換,，得到新的陣元激勵(lì)A(yù)m,。
    (6) 對(duì)Am作截?cái)嗵幚恚槐Ａ羟癕個(gè)數(shù)值,。
    (7) 對(duì)陣元激勵(lì)A(yù)m進(jìn)行歸一化,，其中T個(gè)幅度較大的采樣值置為1，其余置為0,，來(lái)完成陣列的稀疏,。1表示該位置有陣元，0表示該位置無(wú)陣元,。
    (8) 將歸一化的陣元激勵(lì)A(yù)m與迭代前的陣元激勵(lì)進(jìn)行比較,。如果不相同，則執(zhí)行步驟9,；如果相同,，則本次迭代循環(huán)結(jié)束。
    (9) 重復(fù)步驟(3)~步驟(8),，直到PSL達(dá)到給定的旁瓣約束條件,，或迭代次數(shù)達(dá)到給定的一次循環(huán)迭代允許的最大迭代次數(shù)。
    (10) 步驟(2)~步驟(9)為一次迭代循環(huán)步驟,。根據(jù)給定的迭代循環(huán)總次數(shù),，進(jìn)行Num次迭代循環(huán)，就完成了整個(gè)優(yōu)化流程,。
    實(shí)驗(yàn)表明,，一次迭代循環(huán)往往經(jīng)過8~10次迭代便會(huì)結(jié)束，每一次迭代循環(huán)得到的最優(yōu)PSL(局部最優(yōu)PSL)未必能達(dá)到給定的旁瓣約束條件,，但是制定合理的旁瓣約束條件,，就能使局部最優(yōu)PSL接近給定的旁瓣約束。因此只要進(jìn)行足夠多次迭代循環(huán),，每次迭代循環(huán)都以一個(gè)隨機(jī)的初始陣元激勵(lì)數(shù)組開始,，各個(gè)迭代循環(huán)相互獨(dú)立，就有很大的概率得到一個(gè)最優(yōu)或近似最優(yōu)的陣元分布,，取局部最優(yōu)PSL中的最小值作為最后的優(yōu)化結(jié)果,。因?yàn)檫\(yùn)用FFT快速算法計(jì)算方向圖函數(shù)，并且每次迭代循環(huán)的迭代次數(shù)很少,，所以整個(gè)優(yōu)化過程很快就能完成,。
3 計(jì)算機(jī)仿真結(jié)果
　  接下來(lái)分別給出了陣列大小為1 000的大型直線稀疏陣列在不同稀疏率、不同旁瓣約束情況下的優(yōu)化結(jié)果,。仿真參數(shù)為：陣元關(guān)于陣列中心對(duì)稱分布,，陣元均為理想的全向性天線單元，柵格間距d=0.5 λ,，逆FFT與FFT運(yùn)算點(diǎn)數(shù)K=16 384,，迭代循環(huán)總次數(shù)Num=1 000次,。
3.1 仿真結(jié)果
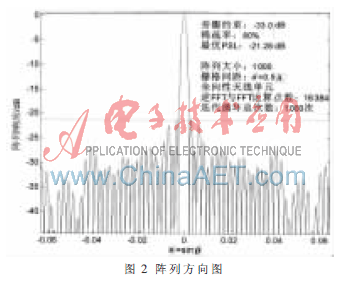
　 (1) 陣列大小為1 000，稀疏率為80%,，旁瓣約束為 －33.0 dB的大型直線稀疏陣列優(yōu)化結(jié)果如圖2所示，得到的最優(yōu)PSL為－21.28 dB,。

 

 

    (2) 陣列大小為1 000,，稀疏率為77%， 旁瓣約束為－32.4 dB的大型直線稀疏陣列優(yōu)化后,得到的最優(yōu)PSL為－23.21 dB,。
　 (3) 陣列大小為1 000,， 稀疏率為66%, 旁瓣約束為－31.4 dB的大型直線稀疏陣列優(yōu)化結(jié)果如圖3所示，得到的最優(yōu)PSL為－27.39 dB,。

　通過對(duì)上述仿真結(jié)果的觀察和比較可以發(fā)現(xiàn),，得到的大型直線稀疏陣列優(yōu)化結(jié)果是符合陣列優(yōu)化規(guī)律的，即在優(yōu)化陣列中,，陣元的稀疏總是發(fā)生在陣列邊緣,，而陣列中心的陣元一般不會(huì)被稀疏掉，并且在一定范圍內(nèi),，稀疏率越小,，所得到的最優(yōu)PSL就越低[5]。
3.2 優(yōu)化方法的性能分析
　 以上所有仿真均在MATLAB7.1中完成,，計(jì)算機(jī)配置為：AMD Phenom(tm)9650 Quad-Core處理器,，主頻為2.3 GHz，每次仿真所花費(fèi)的時(shí)間僅為1 min左右,。圖4為仿真實(shí)驗(yàn)（3）中,，優(yōu)化效果最好、優(yōu)化效果最差,、迭代次數(shù)最少和迭代次數(shù)最多的迭代循環(huán)中的PSL變化情況,。從圖中可以看出，稀疏陣列經(jīng)過較少次迭代后,，其旁瓣性能就能得到很好的改善,。這說(shuō)明了該優(yōu)化方法具有高效性。

    表1給出了陣列大小為1 000,、稀疏率為66%,，旁瓣約束為－31.4 dB的大型直線稀疏陣列20次相對(duì)獨(dú)立的優(yōu)化結(jié)果，其中最好的結(jié)果為－27.39 dB,，最差的結(jié)果為－26.91 dB,，最優(yōu)PSL的平均值為－27.15 dB，方差為0.146 7,。結(jié)果表明每次優(yōu)化得到的最優(yōu)PSL總是在一個(gè)很小的范圍內(nèi)變化,。這說(shuō)明了該優(yōu)化方法具有穩(wěn)健性,。

    迭代FFT算法在解決大型稀疏陣列的優(yōu)化問題上，有其獨(dú)特的優(yōu)勢(shì),。本文使用迭代FFT算法快速地實(shí)現(xiàn)了大型直線稀疏陣列的優(yōu)化設(shè)計(jì),，為同類研究提供了有價(jià)值的參考。仿真結(jié)果證明了該方法的高效性和穩(wěn)健性,。此外,，該優(yōu)化方法還可拓展成2維FFT后應(yīng)用到平面稀疏陣列的優(yōu)化設(shè)計(jì)當(dāng)中。
參考文獻(xiàn)
[1] 王玲玲,方大綱.運(yùn)用遺傳算法綜合稀疏陣列[J].電子學(xué)報(bào),2003,31(12A):2135-2138.
[2] KEIZER W P M N.Large planar array thinning using iterative FFT techniques[J]. IEEE Trans. Antennas Propagation,2009, 57(10):3359-3362.
[3] 徐振華. 相位錐化低旁瓣和差波束方向圖合成新方法[J]. 兵工學(xué)報(bào),2011,32(3):286-291.
[4] KEIZER W P M N. Linear array thinning using iterative FFT techniques[J]. IEEE Trans.Antennas Propagation,2008, 56(8):2757-2760.
[5] 陳客松,何子述,唐海紅.對(duì)稱線陣的優(yōu)化稀疏研究[J].電子與信息學(xué)報(bào),2009,31(6):1490-1492.
[6] Chen Kesong, He Zishu, Han Chunlin. A modified real GA for the sparse linear array synthesis with multiple constraints[J]. IEEE Trans. Antennas Propagation, 2006,54(7):2169-2173.

此內(nèi)容為AET網(wǎng)站原創(chuàng),，未經(jīng)授權(quán)禁止轉(zhuǎn)載,。