醫(yī)學(xué)超聲液性病變圖像多見(jiàn)數(shù)個(gè)無(wú)回聲區(qū)，呈“蜂窩狀”,，邊界不清晰,，為了清晰地提取醫(yī)學(xué)超聲液性病變圖像的邊緣，進(jìn)一步為臨床診斷提供可靠依據(jù),，在此將幾種不同的邊緣檢測(cè)算法應(yīng)用于醫(yī)學(xué)超聲液態(tài)病變圖像中,，經(jīng)實(shí)驗(yàn)結(jié)果得出，經(jīng)典的邊緣檢測(cè)算法不能很好地提取圖像的邊緣,，而基于Snake模型的邊緣檢測(cè)算法,，人為設(shè)定邊緣控制點(diǎn)，智能動(dòng)態(tài)調(diào)整曲線，獲得了很好的邊緣提取效果,，具有很高的臨床應(yīng)用價(jià)值,。
0 引言
鑒于醫(yī)學(xué)圖像可以看到人體組織的局部器官病變，所以醫(yī)學(xué)成像成為疾病檢查的重要手段,，但由于設(shè)備,、技術(shù)等原因，得到的醫(yī)學(xué)圖片邊緣往往模糊不清,，因此醫(yī)學(xué)圖像邊緣檢測(cè)是醫(yī)學(xué)圖像處理和分析的一個(gè)非常重要的分支,。目前醫(yī)學(xué)成像方法主要有：X光成像、核磁共振成像,、超聲成像以及正電子發(fā)射斷層成像,，其中，超聲成像從成像成本,、成像時(shí)間以及對(duì)病人的傷害等方面都顯示出了它的優(yōu)勢(shì),，本文就以醫(yī)學(xué)超聲圖像為例，對(duì)超聲診斷中常見(jiàn)的液性病變圖像進(jìn)行邊緣提取算法分析,。
經(jīng)典的邊緣檢測(cè)算子利用邊緣處一階或二階導(dǎo)數(shù)來(lái)檢測(cè)梯度變化情況,，基本的微分檢測(cè)算子有Roberts算子、Sobel算子,、拉普拉斯算子和Canny算子等,。近年來(lái)，隨著數(shù)學(xué)理論和人工智能的發(fā)展,，又出現(xiàn)了許多新的邊緣檢測(cè)方法,，比如基于分?jǐn)?shù)階微分法、小波變換法,、Snake模型法,、模糊檢測(cè)法、數(shù)學(xué)形態(tài)學(xué)法,、神經(jīng)網(wǎng)絡(luò)法等,。這些邊緣檢測(cè)方法最終目的都是檢測(cè)出圖像的邊緣信息，但在解決特定特征圖像時(shí)也顯現(xiàn)出各自的優(yōu)勢(shì)和不足之處,。所以,，如何采用合適的技術(shù)對(duì)醫(yī)學(xué)圖像進(jìn)行邊緣提取，為臨床醫(yī)生提供更準(zhǔn)確的病人數(shù)據(jù)是目前研究的一個(gè)熱點(diǎn),。
本文首先對(duì)幾種邊緣檢測(cè)方法進(jìn)行分析,，然后將其應(yīng)用于超聲液性病變圖像的邊緣提取中，得出不同的提取效果,，與采用改進(jìn)的Snake模型邊緣提取算法進(jìn)行比較,，實(shí)驗(yàn)表明,，基于Snake模型的邊緣提取算法邊緣提取效果較好。
1 邊緣檢測(cè)算法
邊緣檢測(cè)目的是要檢測(cè)出圖像中灰度變化的不連續(xù)區(qū)域,，確定它們?cè)趫D像中的精確位置,，為后期的圖像分析和處理提供信息，圖像的邊緣包含了物體形狀的重要信息,，主要存在于目標(biāo)與目標(biāo),、目標(biāo)與背景、區(qū)域與區(qū)域(包括不同色彩)之間,，是圖像分割,、紋理特征和形狀特征等圖像分析的重要基礎(chǔ)。圖像邊緣檢測(cè)的實(shí)質(zhì)是采用某種算法來(lái)提取出圖像中對(duì)象與背景間的交界線,。
1．1 基于一階微分的邊緣檢測(cè)算法
圖像中的邊緣通常與圖像強(qiáng)度或圖像強(qiáng)度的一階導(dǎo)數(shù)的不連續(xù)性有關(guān),。圖像強(qiáng)度的不連續(xù)可分為：
(1)階躍不連續(xù)，即圖像強(qiáng)度在不連續(xù)處的兩邊的像素灰度值有著顯著的差異,；
(2)線條不連續(xù),，即圖像強(qiáng)度突然從一個(gè)值變化到另一個(gè)值，保持一個(gè)較小的行程后又返回到原來(lái)的值,。
在一維情況下，階躍邊緣同圖像的一階導(dǎo)數(shù)局部峰值有關(guān),。梯度是函數(shù)變化的一種度量,，而一幅圖像可以看作是圖像強(qiáng)度連續(xù)函數(shù)的取樣點(diǎn)陣列。因此,，圖像灰度值的顯著變化可用梯度的離散逼近函數(shù)來(lái)檢測(cè),。
梯度是一階導(dǎo)數(shù)的二維等效式，定義為向量：
有2個(gè)重要的性質(zhì)與梯度有關(guān)：
(1)向量G(x,，y)的方向就是函數(shù)f(x,，y)增大時(shí)的最大變化率方向；
(2)梯度的幅值由下式給出：
數(shù)字圖像中,，求導(dǎo)數(shù)是利用差分近似微分來(lái)完成的,。根據(jù)模板的大小以及權(quán)值的不同，人們提出了很多梯度算子,，比如Roberts算子,、Sobel算子、Prewitt算子都是基于一階微分的梯度經(jīng)典算子,。
1．1．1 Roberts算子
根據(jù)計(jì)算梯度原理,，采用對(duì)角線方向相鄰2像素之差得到的就是Reberts算子。Roberts算子是22模板的一階微分算子,，是一種斜向偏差分的梯度計(jì)算方法,，梯度的大小代表邊緣的強(qiáng)度，梯度的方向與邊緣走向垂直，因此,，Roberts梯度算子檢測(cè)水平和垂直邊緣的效果好,，定位精度高，但容易丟失部分邊緣,。因?yàn)镽oberts沒(méi)進(jìn)行平滑處理,，對(duì)噪聲較敏感，經(jīng)常會(huì)出現(xiàn)孤立點(diǎn),。用該算子處理邊緣陡峭度高且噪聲小的圖像效果較佳,。
1．1．2 Sobel算子
Sobel算子是使用3 x 3模板的一階微分算子，采用帶權(quán)值的方法計(jì)算差分,，是在Roberts算子的基礎(chǔ)上將方向差分運(yùn)算與局部平均結(jié)合起來(lái)的一種方法,。Sobel算子以f(x，y)為中心的33的鄰域上計(jì)算x和y方向上的偏導(dǎo)數(shù)Gx,，Gy,。利用像素上、下,、左,、右相鄰點(diǎn)的灰度加權(quán)算法，根據(jù)在邊緣點(diǎn)處達(dá)到極值進(jìn)行邊緣檢測(cè),。Sobel算子很容易在空間上實(shí)現(xiàn),，對(duì)噪聲具有較好的平滑作用，能提供比較準(zhǔn)確的邊緣方向信息,，但定位精度不高,，容易產(chǎn)生偽邊緣，其測(cè)得邊緣寬度一般至少為2個(gè)像素,。但由于實(shí)際中很多情形下對(duì)定位精度的要求都不是很高,，因此它是一種較為常用的邊緣檢測(cè)算子。
1．1．3 Prewitt算子
Prewitt和Sobel算子都是使用3×3模板的一階微分算子,，它們是在研究曲面擬合的基礎(chǔ)上提出的,。擬合是指已知某連續(xù)函數(shù)的一系列離散函數(shù)值，通過(guò)最小二乘法等準(zhǔn)則來(lái)確定該函數(shù)中的待定系數(shù),。Prewitt和Sobel算子的2個(gè)差分模板的系數(shù)之間的區(qū)別僅在于求平均的方法不同,。隨后出現(xiàn)的Kirseh算子用不等權(quán)的8個(gè)3×3循環(huán)平均梯度算子分別與圖像進(jìn)行卷積，取其中的最大值輸出,，它可以檢測(cè)各個(gè)方向上的邊緣,，減少了由于平均而造成的細(xì)節(jié)丟失，但同時(shí)增加了計(jì)算量,。
1．2 基于二階微分的邊緣檢測(cè)算法
前面討論了基于一階微分的邊緣檢測(cè),，如果所求的一階微分高于某一閾值,，則確定該點(diǎn)為邊緣點(diǎn)。一階微分組成的梯度是一種矢量,，不但有大小還有方向,，和標(biāo)量比較，數(shù)據(jù)存儲(chǔ)量比較大,。一種更好的方法就是求梯度局部最大值對(duì)應(yīng)的點(diǎn),，并認(rèn)定它們是邊緣點(diǎn)，通過(guò)去除一階微分中的非局部最大值,，可以檢測(cè)出更精確的邊緣,。一階微分的局部最大值對(duì)應(yīng)著二階微分的零交叉點(diǎn)，這意味著在邊緣點(diǎn)處有一階微分的峰值,，同樣地,，有二階微分的零交叉點(diǎn)。這樣,，通過(guò)找圖像強(qiáng)度的二階微分的零交叉點(diǎn)就能找到邊緣點(diǎn),。
在二維空間，對(duì)應(yīng)二階微分有兩種算子：Laplace算子和Marr算子,。Laplace算子也稱拉氏算子,，它的特點(diǎn)是具有旋轉(zhuǎn)對(duì)稱性而不具備方向性，只需要一個(gè)3×3模板,。Laplaee算子是對(duì)二維函數(shù)進(jìn)行運(yùn)算的二階導(dǎo)數(shù)算子,，與方向無(wú)關(guān)，對(duì)取向不敏感,，因而計(jì)算量要小。根據(jù)邊緣的特性,，Laplace算子可以作為邊緣提取算子,，計(jì)算數(shù)字圖像的Laplaee值可以借助模板實(shí)現(xiàn)，但是它對(duì)噪聲相當(dāng)敏感,，它相當(dāng)于高通濾波,，常會(huì)出現(xiàn)一些虛假邊緣。由于Laplace算子存在著諸多缺陷,，它一般并不直接應(yīng)用于邊緣檢測(cè),，而是結(jié)合其它方法以提高邊緣的定位精度。而Marr算子就是在Laplace算子基礎(chǔ)上改進(jìn),，由于它使用的是高斯型的Laplace模板,，因此又被稱作LOG算子，先對(duì)圖像用Gauss函數(shù)進(jìn)行平滑,，然后利用Laplace算子對(duì)平滑的圖像求二階導(dǎo)數(shù)后得到的零交叉點(diǎn)作為待選邊緣,。LOG算子就是對(duì)圖像進(jìn)行濾波和微分的過(guò)程,，是利用旋轉(zhuǎn)對(duì)稱的LOG模板與圖像做卷積，確定濾波器輸出的零交叉位置,。
1．3 Canny算子
Canny算子是最常用的邊緣檢測(cè)方法之一,，是一個(gè)具有濾波、增強(qiáng)和檢測(cè)的多階段的優(yōu)化算子,。
該算法的基本過(guò)程如圖1所示,。
Canny算子檢測(cè)邊緣的實(shí)質(zhì)是求信號(hào)函數(shù)的極大值問(wèn)題來(lái)判定圖像邊緣像素點(diǎn)?；静襟E為：
(1)用高斯濾波器平滑圖像,；
(2)用一階偏導(dǎo)的有限差分來(lái)計(jì)算梯度的幅值和方向；
(3)對(duì)梯度幅值進(jìn)行非極大值抑制,；
(4)用雙閾值算法檢測(cè)和連接邊緣,。Canny算子能夠得到連續(xù)完整的圖像，但需要注意的問(wèn)題是：Gauss濾波的尺度,，以及雙閾值的選擇,。
1．4 基于Snake模型的邊緣檢測(cè)算法
Snake模型是1987年由Kass提出的，它的基本思想是以構(gòu)成一定形狀的控制曲線為模板(或者稱為輪廓線),，通過(guò)模板自身的彈性形變與圖像局部特征相匹配達(dá)到調(diào)和,，即某種能量函數(shù)極小化，完成對(duì)圖像邊緣的提取,，通過(guò)對(duì)模板的進(jìn)一步分析而實(shí)現(xiàn)圖像的理解和識(shí)別,。能量最小化模型已經(jīng)有了很長(zhǎng)的發(fā)展歷史，Kass對(duì)其進(jìn)行了改進(jìn),，采用動(dòng)態(tài)調(diào)整的方法來(lái)實(shí)現(xiàn)它,，對(duì)圖像的高層信息進(jìn)行分析和提取而不至于受到太多低層信息的影響。通過(guò)在原始的最小化函數(shù)中加入外力因子,，可以引導(dǎo)初始化的輪廓線朝著特定的方向前進(jìn),，最后達(dá)到提取目標(biāo)邊界的目的。
1．4．1 基本Snake模型
Kass等提出的基本Snake模型由一組控制點(diǎn)組成,，即v(s)=(x(s),，y(s))，s∈[0,，1],，其中x(s)和y(s)分別表示每個(gè)控制點(diǎn)在圖像中的坐標(biāo)位置，s是以傅立葉變換形式描述邊界的自變量,。其對(duì)應(yīng)的能量函數(shù)定義為：
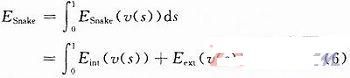
式中：Eint為曲線的內(nèi)部能量,；Eext為外部能量。
內(nèi)部能量定義為：
式中|vs(s)|為彈性能量,，是曲線相對(duì)于弧長(zhǎng)的一階導(dǎo)數(shù)的模,，受彈性系數(shù)的調(diào)節(jié),，控制著曲線的張力。|vss(s)|是彎曲能量,，是曲線相對(duì)于弧長(zhǎng)的二階導(dǎo)數(shù)的模,，受剛性系數(shù)的調(diào)節(jié)，控制曲線的變形程度,。
對(duì)于普通的灰度圖像I(x,，y)，典型的外部能量(外部力)表達(dá)有如下2種定義：
式中▽為梯度算子,，是方差為σ的二維高斯函數(shù),。在圖像邊緣區(qū)域，圖像灰度值的梯度往往較大,，取反后計(jì)算以滿足能量最小的要求,。
每一次迭代，曲線的變形是為了使如下的能量函數(shù)達(dá)到最小化：
彈性能量和彎曲能量合稱內(nèi)部力,，內(nèi)部力用于控制輪廓線的彈性形變,，選取適當(dāng)?shù)膮?shù)α(s)和β(s)將能量函數(shù)ESnake極小化，所對(duì)應(yīng)的v(s)就是對(duì)物體的分割,。在能量函數(shù)極小化過(guò)程中,，彈性能量迅速把輪廓線壓縮成一個(gè)光滑的圓，彎曲能量驅(qū)使輪廓線成為光滑曲線或直線,，而外部力則使輪廓線向圖像的高梯度位置靠攏,，基本Snake模型就是在這3個(gè)力的聯(lián)合作用下工作的。
1．4．2 改進(jìn)的Snake模型
基本Snake模型在應(yīng)用的時(shí)候存在一些缺陷：
(1)要求初始的輪廓線必須與目標(biāo)邊緣非常的接近,，這是因?yàn)槟芰亢瘮?shù)往往會(huì)收斂到一個(gè)非期望的局部最小值,，如果初始的輪廓線離目標(biāo)較遠(yuǎn)，就會(huì)使曲線變形到一個(gè)無(wú)法預(yù)計(jì)的形狀,；
(2)基本Snake模型對(duì)無(wú)法捕獲凹陷邊界,。這樣就限制了Snake模型應(yīng)用到一些存在凹陷區(qū)域的圖像上。
近年來(lái),，針對(duì)以上缺陷，許多研究不僅對(duì)Snake模型本身的能量函數(shù)構(gòu)造和求解算法作了很大改進(jìn),，更在其基礎(chǔ)上衍生出了許多新輪廓線模型,，它們有些在形式上已經(jīng)與基本Snake相去甚遠(yuǎn)，而且也要復(fù)雜得多,，但其指導(dǎo)思想?yún)s是一脈相承的,。比如，Cohen提出了一種氣球力理論,，通過(guò)使用不同尺度的外力場(chǎng),，增加外力場(chǎng)的捕捉范圍,，來(lái)驅(qū)動(dòng)輪廓線向目標(biāo)邊緣逼近。XuChenyang提出的GVF Snake將梯度矢量場(chǎng)(GVF)代替?zhèn)鹘y(tǒng)外力場(chǎng),，讓曲線隨著圖像凹陷的部分而發(fā)生變形,，圈出凹陷的邊緣，由于GVF對(duì)輪廓線的初始位置不是非常的敏感,，尤其對(duì)于二值圖像,，所以它可以很快的收斂到目標(biāo)邊緣，很好地解決了這些問(wèn)題,。
GVF Snake將基本Snake的外部力用擴(kuò)散方程進(jìn)行處理,，得到整個(gè)圖像域的梯度向量場(chǎng)作為外部力，經(jīng)過(guò)擴(kuò)散方程處理后的GVF更加有序,，更能體現(xiàn)物體邊界的宏觀走勢(shì),。由于GVF不是一個(gè)表達(dá)式，無(wú)法用能量函數(shù)的形式求解,，因此GVF Snake是利用力的平衡條件進(jìn)行優(yōu)化,，GVF Snake具有更大的搜索范圍，對(duì)輪廓線初始位置不敏感,，可以分割凹陷的邊界,，對(duì)梯度絕對(duì)值的大小乃至噪聲具有更好的魯棒性，而且它還不必預(yù)先知道輪廓線是要膨脹還是收縮,。
本文將改進(jìn)的GVF Snake模型應(yīng)用于醫(yī)學(xué)超聲液性病變圖像中,，并與其他的邊緣檢測(cè)方法進(jìn)行比較分析。
2 實(shí)驗(yàn)結(jié)果分析
醫(yī)學(xué)超聲診斷出的液性病變多以囊腫為主,，常見(jiàn)的囊腫有甲狀腺囊腫,、卵巢囊腫、肝囊腫等,，這些超聲液性病變圖像灰度變化梯度不大,，多見(jiàn)數(shù)個(gè)無(wú)回聲區(qū)，呈“蜂窩狀”,，邊界不清晰,。
本文選取兩幅具有代表性的肝囊腫、甲狀腺囊腫超聲液態(tài)病變圖像,，用不同的邊緣檢測(cè)算法對(duì)其進(jìn)行處理,，實(shí)驗(yàn)結(jié)果如圖2，圖3所示,。
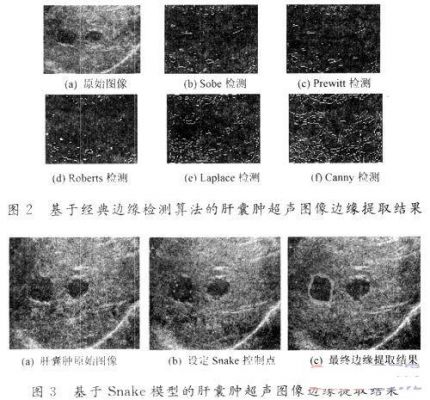
通過(guò)以上兩組實(shí)驗(yàn)可以看出,，由于超聲液態(tài)病變圖像固有特征，經(jīng)典的邊緣檢測(cè)算法并不能清晰的勾畫(huà)出液性病灶的邊緣來(lái),，對(duì)包含病灶區(qū)域的擴(kuò)大區(qū)域?qū)嵤┻吘墮z測(cè)算法,，將得到更多冗余的邊緣信息,，不能得到感興趣病灶區(qū)域的輪廓。而Snake模型卻可以較好地選取特定的區(qū)域,，利用算法特有的曲線變化方式,，最終收攏到雙側(cè)灰度梯度變換平衡點(diǎn)位置，達(dá)到邊緣提取的良好效果,，主要原因在于：
(1)Snake模型可以人為的設(shè)定待提取邊緣的主要控制點(diǎn),，縮小了曲線變化的范圍，更加具有針對(duì)性的對(duì)特定區(qū)域進(jìn)行邊緣提??；
(2)Snake模型對(duì)圖像灰度變化較敏感，在曲線內(nèi)力和外力達(dá)到平衡的情況下,，曲線可以很好的穩(wěn)定在一個(gè)位置,，形成平滑的連續(xù)的曲線。
3 結(jié)語(yǔ)
本文應(yīng)用幾種不同的邊緣檢測(cè)算法提取醫(yī)學(xué)超聲液態(tài)病變圖像的邊緣,，實(shí)驗(yàn)結(jié)果表明,，經(jīng)典邊緣檢測(cè)算法的提取效果不明顯，而基于Snake模型的邊緣提取算法由于采用動(dòng)態(tài)的調(diào)整方法,，提取的圖像邊緣完整,、平滑、清晰,，方便于后續(xù)的診斷性測(cè)量,，具有一定的臨床應(yīng)用價(jià)值，因此,，在臨床使用的醫(yī)學(xué)超聲儀器中,，使用類(lèi)似算法提取液性病變圖像邊緣，將是一個(gè)應(yīng)用趨勢(shì),。
