門限簽名是現(xiàn)代電子商務(wù)中一種重要的數(shù)字簽名,。自門限簽名的思想提出以來,，出現(xiàn)了各種各樣的門限簽名方案。然而,，如何構(gòu)造既高效又抗攻擊的簽名仍然沒有一個(gè)固定的模式,，大多數(shù)方案仍然不能抵御各種內(nèi)部或外部攻擊。如參考文獻(xiàn)[1]提出了一種具有可追查性的抗合謀攻擊門限簽名方案,，參考文獻(xiàn)[2]指出該方案難以抵抗合謀攻擊,；參考文獻(xiàn)[3]提出了一種不可追蹤的抗合謀攻擊方案，參考文獻(xiàn)[4]指出該方案仍存在合謀攻擊問題,。

　    為了進(jìn)一步提高簽名的效率,，參考文獻(xiàn)[5]提出了基于雙線性對(duì)的短簽名。雙線性對(duì)成了構(gòu)造簽名的重要工具,?；陔p線性的簽名方案具有簽字短、安全、高效等特點(diǎn),，它的提出受到了廣泛的關(guān)注,。參考文獻(xiàn)[6]引進(jìn)了PKG的概念，即可信中心,，作用是產(chǎn)生用戶的私鑰,，理論上它必須是完全可信的。大多數(shù)文獻(xiàn)方案的提出也是建立在可信中心的基礎(chǔ)之上,。然而在有些環(huán)境中(如Ad Hoc網(wǎng)絡(luò)),，可信中心并不存在。岳勝等人提出了一種無可信中心門限簽名方案[7](以下簡(jiǎn)稱YUE的方案),。此方案雖有一定的理論價(jià)值,，然而該方案仍存在很大的安全漏洞。同時(shí),，在實(shí)用性方面,，當(dāng)一個(gè)方案受到偽造攻擊時(shí)，良好的可追查性使得簽名能夠有效地檢查成員內(nèi)部的簽名情況,。為此,，本文提出了一種新的具有可追查性的無可信中心(t,n)門限簽名方案。
1 YUE方案的安全性分析
1.1 對(duì)YUE方案的偽造攻擊
　    偽造方案與原簽名方案相似,區(qū)別僅在于在偽造方案中,，辦事員充當(dāng)?shù)氖莻卧旃粽叩纳矸?。在門限簽名生成階段，由于每個(gè)成員本質(zhì)上只起到提供一個(gè)隨機(jī)數(shù)的作用,，辦事員的角色與有可信中心方案中的PKG所起的角色沒有區(qū)別,，而辦事員是在成員內(nèi)部隨機(jī)指定的，因此不可能完全可靠,。下面是辦事員偽造簽名者Pj的部分簽名,，進(jìn)而偽造最終的門限簽名。這里假設(shè)成員Pk是所指定的辦事員,，具體偽造步驟如下:
  
  

                   
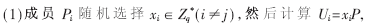
3.2 新方案的安全性
    (1) 簽名不可偽造性
　    任何第三方不能偽造群體對(duì)消息m′進(jìn)行合法的簽名,。由門限簽名合成式(3)可知，即使知道了k′,、H1(m′),，由于不知道∑SIDi，因此仍不能構(gòu)成滿足式(4)的合法門限簽名,。另外,，任何第三方也不能偽造合法成員Pi而進(jìn)行部分簽名。由于在部分簽名生成的過程中,，要用到成員Pi的ki、SIDi，而它們是任何第三方都不能獲知的,，因此無法提交合法的部分簽名
    (2) 方案強(qiáng)壯性
　    本方案在簽名的生成過程中,，用到了只有合法簽名者自己知道的隨機(jī)數(shù)ki，也就無法求得SIDi,。因此,，即使惡意攻擊者賄賂了某些成員，使其在簽名協(xié)議中不按照規(guī)定執(zhí)行,，最后也無法得到正確的簽名,。
3.3 性能分析
    一個(gè)好的門限簽名方案，必須要有很好的強(qiáng)壯性及不可偽造性,，并且在受到攻擊的時(shí)候還要有好的可追蹤性,。同時(shí)計(jì)算量的多少是方案效率高低的重要指標(biāo)，很大程度上影響著方案的可行性,。本方案與原方案的性質(zhì)比較如表1所示,。令Pl、Mu,、Ha,、Pa、Ex分別表示群上的乘法和加法運(yùn)算,、哈希函數(shù)運(yùn)算以及配對(duì)運(yùn)算和指數(shù)運(yùn)算,。本方案與原方案計(jì)算量的比較如表2所示。

    從表1可以看出,，原簽名方案的強(qiáng)壯性和不可偽造性都低于本方案,，同時(shí)，本方案有很好的追蹤性,，而原方案沒有,。從表2可以看出，在部分簽名生成算法中,，YUE方案比本文方案多了一次乘法運(yùn)算,，少t次加法運(yùn)算及2t-1次哈希運(yùn)算。在部分簽名驗(yàn)證算法中,，YUE方案比本文方案多用了2t次乘法運(yùn)算以及2t次指數(shù)運(yùn)算,，少使用t次配對(duì)運(yùn)算及2t次哈希運(yùn)算。在門限簽名驗(yàn)證算法中,，YUE方案比本文方案多使用一次配對(duì)運(yùn)算,，少使用一次指數(shù)運(yùn)算。YUE方案無身份追查,，而本文的身份追查只需t次哈希運(yùn)算,。由以上可以看出,，本文方案總的運(yùn)算量為(4t+1)Mu+(3t-1)Pl+2Ex+(3t+2)Pa+5tHa，岳勝等人的方案總的運(yùn)算量為(6t+2)Mu+(2t-1)Pl+(2t+1)Ex+(2t+3)Pa+Ha,。由此,，本方案總運(yùn)算次數(shù)與YUE方案差不多，但卻非常有效地防治了各種內(nèi)部或外部攻擊,，安全性遠(yuǎn)遠(yuǎn)高于YUE方案,，而且本方案可以簡(jiǎn)易地進(jìn)行身份追蹤，實(shí)用性更強(qiáng),。
3.4 新方案的易追蹤性

    當(dāng)發(fā)生糾紛時(shí),，群中任何成員都只需查看部分簽名中的IDi就可以追查出參加簽名的t個(gè)成員身份。
4 構(gòu)造簽名的思想
    已有大量文獻(xiàn)雖然對(duì)如何構(gòu)造簽名做出了研究,，但至今仍沒有一個(gè)被廣泛認(rèn)可的構(gòu)造簽名方案或策略,。在此，分析幾類容易出現(xiàn)安全問題的簽名構(gòu)造[4],。
    (1)在門限簽名中,，簽名合成者(DC)負(fù)責(zé)部分簽名的合成，同時(shí)負(fù)責(zé)最終簽名的生成,，在有可信中心的簽名方案中還具有派發(fā)密鑰的權(quán)力,。如果簽名合成者和偽造者進(jìn)行合謀，則他們很容易偽造簽名,。因此,，任何門限簽名方案都應(yīng)該考慮對(duì)簽名合成者加以限制。參考文獻(xiàn)[7]提出的門限簽名方案將門限簽名的密鑰發(fā)放權(quán),、簽名合成權(quán)集結(jié)于辦事員,，這樣的權(quán)力分配給簽名方案帶來了安全隱患。
    (2)在構(gòu)造成員的部分簽名或最終簽名時(shí),，應(yīng)盡量使所構(gòu)造簽名的前后參數(shù)具有相關(guān)性,，最好通過不同的函數(shù)運(yùn)算（如哈希函數(shù)、指數(shù)運(yùn)算）來保證簽名參數(shù)的前后關(guān)聯(lián)性,。這樣可以有效地防止各種內(nèi)部或外部攻擊,。
    (3)參考文獻(xiàn)[4]指出為了有效防止中斷協(xié)議攻擊，可以在每次的簽名中附加時(shí)間戳,。同時(shí),，適當(dāng)使用“添加隨機(jī)數(shù)、消息源可識(shí)別數(shù)字簽名”等方法,，可以增加合謀偽造攻擊的難度,。
    本文對(duì)原有的門限簽名進(jìn)行了安全性分析，指出其在構(gòu)造最終的簽名時(shí)前后的參數(shù)沒有關(guān)聯(lián),，導(dǎo)致最終的方案存在安全隱患,。本文提出的新方案構(gòu)造的簽名有效地利用了前后參數(shù)之間的聯(lián)系,，不僅解決了原有方案的缺陷,同時(shí)很好地抵御了各種外部攻擊和內(nèi)部合謀攻擊。
參考文獻(xiàn)
[1] 張文芳,何大可,王宏霞,，等.具有可追查性的抗合謀攻擊門限簽名方案[J].西南交通大學(xué)報(bào),2007,42(4):461-467.
[2] 徐光寶,姜東煥.具有特權(quán)者的門限簽名方案[J].計(jì)算機(jī)工程與應(yīng)用, 2011,47(9):83-85.
[3] Gan Yuanju. Verifiable threshold signature against conspiracy  attack[J].Journal of Zhejiang University Science,2004,5(1): 50-54.
[4] 侯整風(fēng),趙香,楊曦.抗合謀攻擊的門限簽名方案[J].計(jì)算機(jī)工程, 2008,34(17):147-148.
[5] BONEH D, LYNN B, SHACHAM H. Short signatures from  the weil pairing[C].Boyd C. LNCS 2248:Advances in Cryptology Asiacrypt’ 2001. Berlin:Springer,2001:514-532.
[6] SHAMIR A. Identity-based cryptosystems and signature schemes[C]. LNCS 196:Advances in Cryptology-CRYPTO 1984.Berlin:Springer, 1984:47-53.
[7] 岳勝,辛小龍.一種無可信中心門限簽名方案[J].計(jì)算機(jī)工程與應(yīng)用,2011,47(3):87-89.
[8] 達(dá)青峰. 一種標(biāo)準(zhǔn)模型下基于身份的高效門限簽名方案[J].計(jì)算機(jī)工程與應(yīng)用,2010,46(21):76-79.
[9] 呂鑫,王志堅(jiān), 許峰. 基于雙線性對(duì)的新型門限簽名方案[J].計(jì)算機(jī)科學(xué),2011,38(4):111-114.
[10] Liu Danni,Wang Xingwei, Guo Lei, et al. A dynamic  threshold signature scheme with provable security[C]. 2010 2nd International Conference on Future Computer and Communication, 2010:322-324.
[11] 楊長(zhǎng)海.基于身份的門限多代理多盲簽名方案[J].計(jì)算機(jī)工程與應(yīng)用,2010,46(18):121-124.
[12] 王斌,李建華.無可信中心的門限簽名方案[J].計(jì)算機(jī)學(xué)報(bào), 2003,26(11):1581-1584.
[13] 楊勝良.Lagrange插值公式的幾種構(gòu)造性證明[J]. 大學(xué)數(shù)學(xué),2004,20(3):47-50.