摘 要: 研究討論了用于麥克風(fēng)陣列的高信噪比定向采音算法,設(shè)計(jì)實(shí)現(xiàn)了麥克風(fēng)陣列語音采集系統(tǒng)。通過對(duì)采集到的空間中不同方向音頻進(jìn)行數(shù)字信號(hào)處理,使陣列形成的波束主瓣指向目標(biāo)語音,零陷指向干擾源,提高采音信噪比,實(shí)現(xiàn)對(duì)聲源的定向采音等。測(cè)試結(jié)果表明,本系統(tǒng)采音效果良好,采集到的聲音信號(hào)主瓣很窄,能夠?qū)崿F(xiàn)高信噪比定向采音。
關(guān)鍵詞: 麥克風(fēng)陣列;語音處理;SMI算法;定向采音
目前,在語音采集場(chǎng)合中(如舞臺(tái)、大型會(huì)議室、電視會(huì)議等)通常使用孤立麥克風(fēng)作為語音拾取工具。但是孤立麥克風(fēng)會(huì)采集環(huán)境噪音,在多音源場(chǎng)合中相互干擾難以避免,這些缺陷嚴(yán)重影響了語音采集質(zhì)量。隨著陣列信號(hào)處理技術(shù)[1]的發(fā)展,利用麥克風(fēng)陣列拾取語音信號(hào)為提高采音質(zhì)量提供了可能[2]。通過陣列信號(hào)處理的方法能夠?qū)崿F(xiàn)智能的語音信號(hào)優(yōu)化效果,實(shí)現(xiàn)語音定向采集,提高信噪比。
目前,麥克風(fēng)陣列語音信號(hào)處理技術(shù)是語音采集技術(shù)領(lǐng)域的一個(gè)研究熱點(diǎn)。CHANG A C和HUNG J C等[3]研究了MUSIC語音信號(hào)陣列處理算法,在理論上證明了能夠提高采音精度,具備信號(hào)選擇和提取等性能。GANNOT S和COHEN I等[4]研究了基于廣義旁瓣抵消器結(jié)構(gòu)的語音增強(qiáng)的算法,認(rèn)為GSC算法能夠很好地提高采音信噪比。邵懷宗等[5]設(shè)計(jì)了一種12陣元麥克風(fēng)陣列,提高了采音精度。楊祥清等[6]提出的三維聲源定位系統(tǒng)減少了陣元數(shù)量,同時(shí)保持了一定的采音精度。但國(guó)內(nèi)尚無具有自主知識(shí)產(chǎn)權(quán)的產(chǎn)品,所以研究麥克風(fēng)陣列語音采集系統(tǒng)具有較高的市場(chǎng)價(jià)值。
本文從上述應(yīng)用背景出發(fā),分析了基于麥克風(fēng)陣列的高信噪比定向采音系統(tǒng)所涉及的相關(guān)算法,重點(diǎn)討論了軟硬件系統(tǒng)的工程實(shí)現(xiàn)。麥克風(fēng)陣列定向采音算法主要有自適應(yīng)波束形成技術(shù)中的最小均方(LMS)算法和采樣自相關(guān)矩陣求逆(SMI)算法[7]等。自適應(yīng)陣列的性能與算法的收斂速度密切相關(guān)。為了加快收斂速度并解決收斂速度依賴于特征值分布的問題,常采用基于信號(hào)環(huán)境的采樣自相關(guān)矩陣求逆(SMI)算法。本文采用SMI算法,應(yīng)用易于生產(chǎn)、精度高于二維定位、實(shí)用性更強(qiáng)的4陣元麥克風(fēng)陣列,并使用DSP進(jìn)行陣列信號(hào)處理,以滿足對(duì)聲源信息定向采集的需求。
1 算法模型
自適應(yīng)波束形成算法應(yīng)用于麥克風(fēng)陣列語音采集系統(tǒng)時(shí),能夠隨信號(hào)源的變化自動(dòng)調(diào)節(jié)有關(guān)參數(shù),從而達(dá)到調(diào)節(jié)方向圖主瓣方向的目的。該算法主要是對(duì)采集到的麥克風(fēng)陣列信號(hào)運(yùn)行內(nèi)部反饋控制,并根據(jù)一定的準(zhǔn)則形成權(quán)向量,通過對(duì)接收到的信號(hào)進(jìn)行加權(quán)疊加,使陣列方向圖的波束主瓣指向有用信號(hào),零陷或較低的旁瓣指向干擾信號(hào)方向[8],從而將不同的信號(hào)從空間上實(shí)現(xiàn)分隔,實(shí)現(xiàn)定向采音。
1.1 陣列模型
本系統(tǒng)采用等距線性麥克風(fēng)陣列[9]。對(duì)于實(shí)際使用的陣列結(jié)構(gòu)要求方向向量a(θ)與入射角θ一一對(duì)應(yīng),不能出現(xiàn)模糊現(xiàn)象。因此,陣元間距d不能任意選擇,有時(shí)甚至需要非常精確地校準(zhǔn)。假設(shè)d很大,則相鄰陣元的相位延遲會(huì)超過2π,此時(shí),陣列方向向量無法在數(shù)值上分辨出具體的相位延遲,就會(huì)出現(xiàn)相位模糊[10]。對(duì)于等距線性陣列來說,其陣元間距不能大于半波長(zhǎng)λ/2。
語音的主要頻率范圍為340 Hz~4 000 Hz ,空氣中聲速約為 C=340 m/s,可得波長(zhǎng)的范圍為0.085 m~1 m,因此d的范圍為4.25 cm~50 cm。而對(duì)于低旁瓣或零深陷的復(fù)雜波束,要求r=10L2/λ(r為聲源到基陣的距離,L為等距線性陣列長(zhǎng)度)或更大距離[11],考慮應(yīng)用環(huán)境,取r范圍為2 m~10 m。經(jīng)測(cè)試發(fā)現(xiàn),一般人說話的聲音頻率在1 000 Hz左右,即λ在0.34 m左右。由此可以推算出L為0.26 m~0.58 m。因此取L=45 cm。
建立等距線性陣列模型,該信號(hào)在發(fā)射端表示為s(t),信道復(fù)增益(包括幅度和相位影響)為h(t),入射角為θ,以圖1表示M陣元直線型麥克風(fēng)陣列。


1.3 算法仿真
使用MATLAB軟件對(duì)SMI算法進(jìn)行仿真。圖2所示為信號(hào)源方向?yàn)?°,主要干擾信號(hào)方向?yàn)?5°的8陣元(圖2(a))與4陣元(圖2(b))麥克風(fēng)陣列仿真結(jié)果。

由圖2可以看出,該算法在45°方向形成了零陷,有效地抑制了主干擾信號(hào)。而在0°方向形成了具有一定寬度的主瓣,由于主瓣的增益大于所有旁瓣的增益,因此該算法能有效地采集到期望信號(hào),抑制其他信號(hào)。
雖然,8陣元的仿真結(jié)果比4陣元的要好,主瓣較窄,零陷明顯,但是算法復(fù)雜度較高,硬件實(shí)現(xiàn)較為困難。綜合仿真結(jié)果和硬件電路復(fù)雜度,認(rèn)為采集信號(hào)的麥克風(fēng)的個(gè)數(shù)為4個(gè),每個(gè)麥克風(fēng)的間距為15 cm時(shí),該算法的性能較好,且硬件電路較容易實(shí)現(xiàn)。
2 硬件實(shí)現(xiàn)
2.1 系統(tǒng)整體方案
圖3為系統(tǒng)硬件結(jié)構(gòu)圖,包括4陣元直線型麥克風(fēng)陣列、4路音頻放大濾波電路、DSP處理器以及音頻編解碼器。
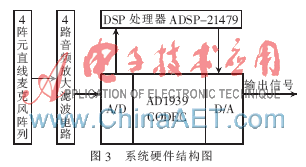
麥克風(fēng)陣列采用4個(gè)駐極體式麥克風(fēng)構(gòu)成陣列;放大濾波電路對(duì)麥克風(fēng)陣列采集到的信號(hào)進(jìn)行預(yù)處理,通過RCA端子將預(yù)處理后的信號(hào)送往音頻編解碼器;處理器采用ADSP-21479,用SMI算法對(duì)量化編碼后的4路音頻信號(hào)進(jìn)行處理,得到期望信號(hào);音頻編解碼器AD1939對(duì)經(jīng)過放大濾波后的4路音頻信號(hào)進(jìn)行量化編碼,隨后將DSP的處理結(jié)果經(jīng)D/A轉(zhuǎn)換后輸出。
2.2 關(guān)鍵模塊設(shè)計(jì)
2.2.1 DSP處理器與系統(tǒng)程序
數(shù)字波束形成[12]的過程是一系列矩陣相乘的過程,其運(yùn)算的數(shù)據(jù)量大,而信道環(huán)境是不斷變化的,導(dǎo)致最優(yōu)權(quán)值也處于不斷的變化中,因此實(shí)際權(quán)值必須進(jìn)行不斷的調(diào)整,因而要求瞬時(shí)處理速度要快。
DSP處理技術(shù)[13]可以運(yùn)用在對(duì)瞬時(shí)處理能力要求更加苛刻的環(huán)境,DSP處理器和通用處理器最大的不同在于數(shù)據(jù)處理能力的增強(qiáng),其核心是對(duì)連續(xù)存儲(chǔ)的數(shù)據(jù)依次作重復(fù)的乘加運(yùn)算[14]。
另外,由于浮點(diǎn)型DSP處理器具有運(yùn)算精度高等特點(diǎn),因此本系統(tǒng)選擇ADI公司的高性能浮點(diǎn)DSP處理器ADSP-21479芯片作為整個(gè)系統(tǒng)的核心。ADSP-21479是高性能32/40 bit浮點(diǎn)處理器,具有高性能音頻處理的功能;工作頻率高達(dá)300 MHz,滿足實(shí)時(shí)性的要求;另外,還具有精簡(jiǎn)的指令集,編程較容易。
由于陣列信號(hào)處理是在信號(hào)的復(fù)基帶進(jìn)行的,需要進(jìn)行大量的復(fù)數(shù)運(yùn)算,因此如果沒有簡(jiǎn)潔、優(yōu)化的執(zhí)行程序,算法的運(yùn)算時(shí)間就會(huì)比較長(zhǎng)。在本設(shè)計(jì)中,考慮到矩陣運(yùn)算的復(fù)雜性,采用C語言進(jìn)行編程。采用這種方式,可縮短軟件開發(fā)的時(shí)間,提高程序的可讀性和可移植性,但是在滿足系統(tǒng)實(shí)時(shí)運(yùn)算的要求上會(huì)有所缺陷。
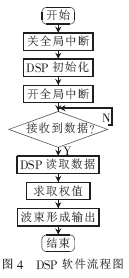
基于上述討論,DSP采用圖4所示的流程圖實(shí)現(xiàn)自適應(yīng)波束形成。
2.2.2 前置放大濾波電路
由于駐極體麥克風(fēng)采集到的信號(hào)存在嚴(yán)重噪音,為了獲得高質(zhì)量的音頻信號(hào),在DSP板載RCA輸入端子前加了前置放大濾波電路對(duì)語音信號(hào)進(jìn)行預(yù)處理。經(jīng)測(cè)試,放大濾波電路通頻帶為0~1 300 Hz,放大倍數(shù)為0~54 dB可調(diào),典型值約為46 dB,該電路可以有效降低噪聲的干擾,從而提高音質(zhì)。
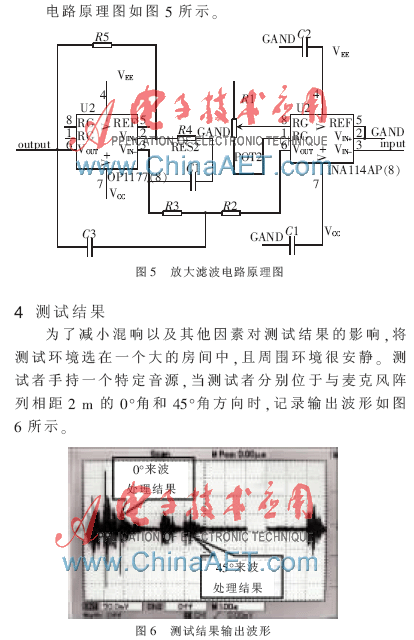
從圖6可以看出,對(duì)于同樣距離的同一聲源,在主瓣(即0°方向)可以實(shí)現(xiàn)最大輸出,而在形成零陷的45°方向?qū)?shí)現(xiàn)抑制。這個(gè)測(cè)試結(jié)果與圖2所示的仿真結(jié)果相吻合。這樣就實(shí)現(xiàn)了波束的形成,進(jìn)而實(shí)現(xiàn)定向采音。
基于麥克風(fēng)陣列的定向采音技術(shù)是一個(gè)新興的領(lǐng)域,具有深刻的技術(shù)背景和廣闊的應(yīng)用前景。本文從算法模型到硬件實(shí)現(xiàn)詳細(xì)介紹了基于麥克風(fēng)陣列的高信噪比定向采音系統(tǒng)。本系統(tǒng)可以給出較好的采音效果,硬件實(shí)現(xiàn)也不復(fù)雜。在基于麥克風(fēng)陣列的定向采音技術(shù)上,本系統(tǒng)還可以進(jìn)行一些改進(jìn)。在理論上,可以進(jìn)一步提高定向采音精度,更快速地跟蹤及更有效地去噪;在實(shí)現(xiàn)上,因?yàn)樯婕岸嗤ǖ勒Z音處理和更為復(fù)雜的核心算法,需要實(shí)現(xiàn)更加苛刻的實(shí)時(shí)信號(hào)處理要求。
參考文獻(xiàn)
[1] KRIM H, VIBERG M. Two decades of array signal processing research: the parametric approach[J]. Signal Processing Magazine, IEEE, 1996,13(4):67-94.
[2] KANEDA Y, OHGA J. Adaptive microphone-array system for noise reduction[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1986,34(6):1391-1400.
[3] CHANG A C, HUNG J C. DOA estimation using iterative MUSIC algorithm for CDMA signals[J]. IEICE Transactions on communications, 2009, 92(10): 3267-3269.
[4] GANNOT S, COHEN I. Speech enhancement based on the general transfer function GSC and postfiltering[J]. IEEE Transactions on Speech and Audio Processing, 2004,12(6):561-571.
[5] 邵懷宗,林靜然,彭啟琮,等.基于麥克風(fēng)陣列的聲源定位研究[J].云南民族大學(xué)學(xué)報(bào)(自然科學(xué)版),2004,13(4):256-258.
[6] 楊祥清,汪增福.基于麥克風(fēng)陣列的三維聲源定位算法及其實(shí)現(xiàn)[J].聲學(xué)技術(shù),2008,27(2):260-265.
[7] 桑懷勝,李崢嶸.智能天線的原理、自適應(yīng)波束形成算法的研究進(jìn)展與應(yīng)用[J].國(guó)防科技大學(xué)學(xué)報(bào),2001,23(6):83-89.
[8] GRIFFITHS L, JIM C. An alternative approach to linearly constrained adaptive beamforming[J]. IEEE Transactions on Antennas and Propagation, 1982,30(1): 27-34.
[9] 王冬霞,趙光,鄭家超.麥克風(fēng)陣列拓?fù)浣Y(jié)構(gòu)對(duì)語音增強(qiáng)系統(tǒng)性能影響的理論分析[J].遼寧工業(yè)大學(xué)學(xué)報(bào)(自然科學(xué)版),2010,30(1):1-4.
[10] BALLAL T, BLEAKLEY C. Phase-difference ambiguity resolution for a single-frequency signal in the near-field using a receiver triplet[J]. IEEE Transactions on Signal Processing, 2010,58(11):5920-5926.
[11] KENNEDY R A, ABHAYAPALA T D, WARD D B.Broadband nearfield beamforming using a radial beampattern transformation[J]. IEEE Transactions on Signal Processing, 1998,46(8): 2147-2156.
[12] TURCOTTE R L, MA S C H, AGUIRRE S. Method and intelligent digital beam forming system with improved signal quality communications[P]. Google Patents,5856804: 1999-01-05.
[13] RABINER L R, GOLD B. Theory and application of digital signal processing[M]. Englewood Cliffs, NJ, Prentice-Hall, Inc., 1975.
[14] 劉書明,蘇濤,羅軍輝.TigerSHARC DSP應(yīng)用系統(tǒng)設(shè)計(jì)[M].北京:電子工業(yè)出版社,2004.

