《電子技術(shù)應(yīng)用》
您所在的位置：首頁 > 嵌入式技術(shù) > 設(shè)計應(yīng)用 > 基于圖像處理的跳頻信號參數(shù)估計
基于圖像處理的跳頻信號參數(shù)估計
來源：電子技術(shù)應(yīng)用2013年第1期
殷 婕1, 龔曉峰1, 武瑞娟2, 馮 霞3
1. 四川大學(xué) 電氣信息學(xué)院，四川 成都 610065； 2. 成都華日通訊技術(shù)有限公司,， 四川 成都610065； 3. 長虹技術(shù)中心,， 四川 綿陽 621000
摘要： 針對復(fù)雜的電磁環(huán)境對跳頻信號檢測所產(chǎn)生的影響，提出了一種新的基于圖像處理的跳頻信號參數(shù)估計方法,。首先將短時傅里葉變換（STFT）后的時頻圖處理為二維圖像,，然后根據(jù)電磁環(huán)境中噪聲在時頻圖中的表現(xiàn)形式，對時頻圖進行濾波處理,，最后根據(jù)對時頻圖的分析得出跳頻信號參數(shù)估計,。使用真實數(shù)據(jù)所進行的實驗結(jié)果表明，所提出的方法能有效地濾除實際跳頻信號中的霧態(tài)噪聲,、定頻和突發(fā)信號,，且不需要知道信號的跳速或駐留時間等前提條件，運算原理清晰,，時間成本低且具有較高的準確度,。目前該方法已應(yīng)用于某數(shù)字接收機產(chǎn)品中，能很好地滿足實際需求及測量精度要求,。
中圖分類號： TN914.41
文獻標(biāo)識碼： A
文章編號： 0258-7998(2013)01-0083-03
A parameter estimation for frequency-hopping signals based on image processing
Yin Jie1, Gong Xiaofeng1, Wu Ruijuan2,， Feng Xia3
1.School of Electrical Engineering and Information, Sichuan University, Chengdu 610065, China; 2.Chengdu Huari Communication Technology Co.,Ltd.， Chengdu 610065, China; 3. Changhong Technology Center, Mianyang 621000, China
Abstract： In order to reduce the impact of the complicated electromagnetic environment on the frequency hopping (FH) signal detection, a new FH signals based on image processing parameter estimation method is proposed. The short time Fourier transform (STFT) time-frequency diagram is treated as a two-dimensional image. Then make filter processing on the image according to the form that the noise in the electromagnetic environment express in the frequency diagram. Finally, the parameters of the FH signal is given according to the diagram of time-frequency signal. Experiment which using the real signal indicates that the proposed method can filter out the actual FH signals in fog mode noise, constant frequency and burst signal. It doesn’t need to know some preconditions such as hop-rate, dwell-time at all.This method enjoys the advantages of low computational complexity, simple implementation and high accuracy. This method has the practical application of a digital receiver products, well positioned to meet the actual demand and the measurement accuracy.
Key words : frequency-hopping detection; image processing; STFT; time-frequency analysis

    跳頻通信具有良好的抗多徑,、抗衰落、抗干擾,、低截獲率和易于組網(wǎng)等特點,，因此其在軍事和民用通信方面得到了極大的應(yīng)用和發(fā)展。

    由于多頻率分量信號處理中被廣泛使用的魏格納威爾分布WVD(Wigner-Ville Distribution)會產(chǎn)生交叉項問題,，嚴重影響信號檢測結(jié)果,，因此許多研究采用改進的WVD方法[1-3]，這些改進算法雖然能降低交叉項的影響 ,，但運算量過大,，且有的算法會導(dǎo)致時間分辨率及頻率分辨率受到嚴重影響。參考文獻[4]提出了一種基于自回歸自適應(yīng)譜估計模型的跳頻信號檢測方法;參考文獻[5]提出利用信號STFT的結(jié)果得到其峰值序列來進行跳頻信號的跳周期估計,；參考文獻[6]采用了時頻分析與圖像處理相結(jié)合的算法,，有效地通過圖像分割等技術(shù)提取出了跳頻信號，但由于未考慮到實際環(huán)境中所存在的噪聲干擾等問題對跳頻信號檢測的影響,，使其實用性受到局限,。
    本文提出用短時傅里葉變換(STFT)對跳頻信號進行分析,，利用現(xiàn)在較為完善的圖像處理技術(shù)與時頻分析相結(jié)合，濾除雜散噪聲及定頻,、突發(fā)號,，再根據(jù)時頻圖中信號在時間軸和頻率軸上的投影求出頻率集，利用跳時刻差分的均值來估計跳周期并通過實驗給出了估計性能,。并且目前大多數(shù)文章所提出的方法都只是建立在仿真分析的基礎(chǔ)上,，缺乏實際應(yīng)用驗證。而本文提出的方法已應(yīng)用于實際產(chǎn)品中,，其穩(wěn)定性和精度均能滿足需求,，具有較高的實際意義。
1 跳頻信號的檢測及分析
1.1 短時傅里葉變換
    跳頻信號是一種非平穩(wěn)信號,，傳統(tǒng)的傅里葉變換對它的處理具有信號的時域與頻域信息不能同時局部化等局限性,。而時頻分析[7]作為分析時變非平穩(wěn)信號的有力工具，近年來受到越來越多的重視,，已成為跳頻通信研究中常用的分析手段,。其中STFT計算量小、時頻聚集性較好,，從時頻圖中可以較為明確地分析信號特征,，應(yīng)用最為廣泛。

    根據(jù)W.Heisenberg不確定性原理,，短時傅里葉變換的時間分辨率和頻率分辨率互相矛盾,，應(yīng)當(dāng)根據(jù)實際情況來考慮時間分辨率及頻率分辨率的大小。對非平穩(wěn)信號,，若信號變化劇烈,，要求窗函數(shù)有較高的時間分辨率；而波形變化比較平緩時,，則要求窗函數(shù)有較高的頻率分辨率,。因此，窗函數(shù)的選取十分重要,，窗越寬,，時間分辨率越差；反之則會降低頻率分辨率,。
1.2 對時頻圖進行圖像處理
    通過短時傅里葉變換得到的時頻圖,，可以將其視為一幅二維圖像。復(fù)雜的電磁環(huán)境中存在許多噪聲會對跳頻信號的檢測造成較大干擾,，而這些噪聲信號在時頻圖中的表現(xiàn)形式各有不同,。在時頻圖中不同頻率上彼此銜接的短線段為跳頻信號，每一段短線段即為一跳;圖中除跳頻信號外,，在同一頻率連續(xù)出現(xiàn)的長線段為定頻信號,；一系列較細的斜線段為掃頻信號,；由噪聲的隨機性產(chǎn)生的霧態(tài)噪聲，在時頻圖上為隨機分布的零散能量,。因此,，從實際環(huán)境中剔除噪聲信號演變成為對時頻圖進行圖像相關(guān)處理。
    數(shù)學(xué)形態(tài)學(xué)是基于集合論的圖像處理分析方法,，可以保持所需圖形的基本形狀特性,，并除去不相干的結(jié)構(gòu)，并且可以大大提高圖像分析和處理的速度,。本文選用其中的開,、閉運算來對時頻圖進行濾波處理。


    為了從復(fù)雜的信道環(huán)境中提取出跳頻信號,，應(yīng)對時頻圖進行進一步的形態(tài)學(xué)濾波處理,。首先進行圖像開處理，以濾除霧態(tài)噪聲,。通過實驗驗證,，開運算的結(jié)構(gòu)元素選擇寬625個點，高1個頻率分辨率的矩形效果較好,，經(jīng)過開處理后的時頻圖如圖2所示,。其次進行圖像閉處理，提取定頻信號,。閉運算的結(jié)構(gòu)元素選擇寬375個點,，高1個頻率分辨率的矩形窗。經(jīng)過閉運算后提取出來的定頻信號,。這樣的結(jié)構(gòu)元素能夠抑制譜圖中的波谷噪聲,，填平雜散負脈沖；也符合跳頻信號形態(tài)特征,，在一定程度上恢復(fù)了由去干擾處理導(dǎo)致的信號形態(tài)缺失,。

 

 

    再將除去雜散噪聲后的時頻圖與提取出的定頻信號進行式(7)的運算，便可以提取出跳頻信號,，如圖3所示,?？梢钥闯?，通過形態(tài)學(xué)處理，噪聲剔除效果較好,，且基本未對原有的跳頻信號產(chǎn)生影響,。在求取跳周期時，由圖3跳頻信號時頻圖可以看出,，信號存在第一跳和最后一跳兩個不完整的跳頻周期,，它們會對跳頻周期的估計產(chǎn)生較大的影響,，而這兩跳之間的跳頻信號都是完整的,對跳頻周期的估計沒有影響。所以在估計跳頻周期的過程中,，用第一跳與最后一跳之間的跳時刻的差分均值求取跳周期,。
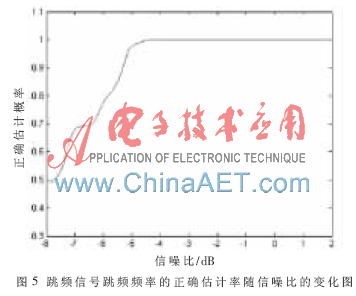
    為驗證本文方法在不同信噪比的情況下對跳頻參數(shù)估計性能的影響，對[-8 dB,2 dB]之間的不同信噪比下的信號分別進行100次實驗,，得到跳頻信號跳周期的正確估計率隨信噪比的變化圖,，如圖4所示。從圖4中可以看出,，當(dāng)信噪比高于-3 dB之后,，對跳頻信號跳周期的正確估計率達到95%以上。跳頻信號跳頻頻率的正確估計率隨信噪比的變化如圖5所示,。由圖5可知,，當(dāng)信噪比高于-5 dB之后，對跳頻信號跳頻頻率的正確估計率達到98%以上,。

    本文在實際應(yīng)用背景下提出了一種跳頻信號檢測及參數(shù)估計的方法,，理論分析和現(xiàn)場應(yīng)用表明，本文方法能有效消除復(fù)雜的電磁環(huán)境中所存在的噪聲干擾,，且估計精度較高,，運算量小，把算法應(yīng)用于實際工程中,，更具有工程價值,。
參考文獻
[1] 趙俊,張朝陽，賴利峰,等. 一種基于時頻分析的跳頻信號參數(shù)盲估計方法[J].電路與系統(tǒng)學(xué)報, 2003,8(3)：46-50.
[2] 馮濤,袁超偉. 跳頻信號的時頻分析新方法[J].北京郵電大學(xué)學(xué)報, 2010,33(3):10-14.
[3] 陳超,郝雁中,高憲軍,等. 基于WVD改進算法的跳頻信號參數(shù)估計[J].吉林大學(xué)學(xué)報,2010,28(2):124-130.
[4] 黃東巍,邵定蓉,李暑堅. 基于自適應(yīng)譜估計的跳頻捕獲技術(shù)[J].北京航空航天大學(xué)學(xué)報,2006,32(5):540-543.
[5] 嚴超會,湯建龍. 跳頻信號的跳周期估計[J].信息與電子工程,2011,9(1):74-77.
[6] Xu Mankun, Ping Xijian, Li Tianyun, et al. A new time frequency spectrogram analysis of FH signals by image enhancement and mathematical morphology[C]. Fourth International Conference on Image and Graphics, 2007:610-615.
[7] BARBAROSSA S, SCAGLIONE A. Parameter estimation of spread spectrum frequency hopping signals using time-frequency distributions[C].First IEEE Signal Processing Working on Signal Processing Advances in Wireless Communications, 1997:213 -216.
[8] 朱文貴, 戴旭初, 徐佩霞.  一種跳頻信號參數(shù)估計的方法[J].小型微型計算機系統(tǒng),2008,29(4):761-764.

此內(nèi)容為AET網(wǎng)站原創(chuàng),，未經(jīng)授權(quán)禁止轉(zhuǎn)載,。