摘 要: 壓縮感知打破了傳統(tǒng)采樣定理的限制,提供了一種從少量的非自適應線性測量值中就能恢復原始信號的方法,。測量矩陣正是獲取這些測量值的關鍵所在,,尋求結構簡單、性能穩(wěn)定的測量矩陣一直是研究人員的目標,。在介紹壓縮感知測量矩陣的基礎上,,提出了廣義輪換矩陣的改進方法,結合正交基線性表示的思想,,利用廣義輪換構造的正交矩陣來生成新的測量矩陣,。通過仿真實驗,證明了新的測量矩陣具有較好的性能,。
關鍵詞: 壓縮感知,;稀疏信號;測量矩陣,;廣義輪換矩陣,;正交基
2004年,Donoho D[1]和Candès E[2]等人在泛函分析和逼近論的基礎上,,結合信號稀疏表示理論提出了一個全新的信號采樣理論,,即壓縮感知CS(Compressed Sensing)[1-2]。與傳統(tǒng)的Nyquist采樣定律不同,,壓縮感知同時完成了對信號的采樣和壓縮,,在信號的采樣階段就很好地避免了大量冗余數(shù)據(jù)的產生。壓縮感知一經提出,,就引起人們的廣泛關注,,在信息技術飛速發(fā)展的今天,有著廣闊的發(fā)展前景,。在壓縮感知理論中,,信號的采樣速率不再取決于信號的帶寬,而是取決于信號本身的結構和特性(稱為稀疏性,或可壓縮性),。其核心思想是:當信號具有稀疏性或可壓縮性時,,就可以通過一個非自適應的線性測量過程將原信號映射到低維空間,得到少量的測量值,,然后通過求解一個稀疏最優(yōu)化問題就可以恢復原始信號,。
總地來說,壓縮感知過程包括3個主要問題:信號的稀疏表示,、信號的線性測量和信號的重建,。本文主要研究信號的線性測量,并介紹壓縮感知測量矩陣,。


(1)隨機測量矩陣:如高斯矩陣[1,,4]、貝努利矩陣[4]等,。隨機矩陣可以用較少的采樣值獲得精確的重建,,但是隨機測量矩陣自身存在的不確定性會給矩陣存儲和硬件實現(xiàn)帶來困難,也會造成仿真實驗的不確定性,。
(2)確定性測量矩陣:如多項式測量矩陣[5]等,。相比隨機測量矩陣,確定性測量矩陣可以節(jié)省存儲空間,,易于硬件實現(xiàn),,也更易于設計快速算法,但是其重建效果較差,,精確重建需要的測量值較多,。
(3)部分隨機測量矩陣:如部分正交矩陣[6]、部分哈達瑪矩陣[4],、托普利茲和輪換矩陣[7]等。部分隨機矩陣既有部分的隨機性,,又兼具一定的確定性,,性能較好,硬件實現(xiàn)也相對容易,。


3 仿真實驗和結果
為了驗證構造的新測量矩陣的性能,,采用Matlab圖像庫中提供的標準256×256 Lena圖像進行仿真實驗。首先利用小波變換對原圖像進行稀疏化處理,,然后分別選用新矩陣,、部分哈達瑪、托普利茲,、廣義輪換,、部分正交等測量矩陣對稀疏化后的圖像進行測量,最后采用OMP[10]重建算法對壓縮后的圖像信號進行恢復,得到恢復圖像,。針對壓縮比M/N≤0.5的情況,,得到圖1所示的峰值信噪比(PSNR)性能比較圖。
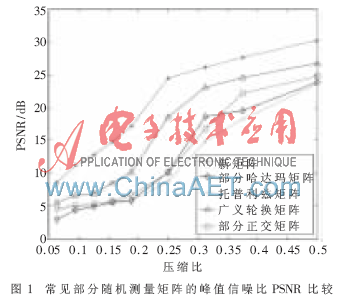
由實驗結果可以看出,,廣義輪換矩陣的性能要優(yōu)于其他測量矩陣,,而因為新的測量矩陣是由廣義輪換矩陣改進了向量原子后得到的,所以針對不同的壓縮比,,新矩陣的性能變化曲線與廣義輪換矩陣相似,,但整體性能要比廣義輪換矩陣高出3 dB左右。在壓縮比較小時,,新矩陣相比于其他測量矩陣具有更突出的優(yōu)勢,,驗證了確定數(shù)+高斯隨機數(shù)的偽隨機數(shù)更適合這種壓縮比較小的情況。整體而言,,對于壓縮比M/N≤0.5的情況,,新的測量矩陣在和其他部分測量矩陣的對比中表現(xiàn)出了更好的性能。
圖2給出了256×256 Lena圖像的原始圖像和利用新的測量矩陣測量后恢復的圖像,,此處選擇壓縮比M/N=0.5,,此時的峰值信噪比PSNR達到了30.28。

本文旨在研究壓縮感知中的測量矩陣,,改進了廣義輪換矩陣的向量原子,,結合正交基線性表示的構造方法,提出用確定數(shù)+隨機數(shù)的偽隨機數(shù)作為正交基系數(shù),,構造了新的測量矩陣——基于正交基線性表示的二進制生成矩陣,。首先,改進廣義輪換矩陣向量原子,,采用二進制1和0交替的向量原子,,矩陣更稀疏,硬件實現(xiàn)更簡單,;然后,,結合正交基線性表示的思想,將廣義輪換構造的正交矩陣作為正交基,,針對M/N≤0.5的情況,,提出采用確定數(shù)+隨機數(shù)組合的偽隨機數(shù)作為線性系數(shù),構造出新的測量矩陣,。選擇二維圖像數(shù)據(jù)進行仿真實驗,,應用不同測量矩陣進行對比,實驗結果顯示新的測量矩陣擁有更好的性能,。
參考文獻
[1] DONOHO D.Compressed sensing[J].IEEE Transaction on Information Theory,,2006,,52(4):1289-1306.
[2] CANDES E.Compressive sampling[A].Proceedings of the international congress of mathematicians[C].Madrid,Spain,,2006:1433-1452.
[3] CANDES E,,ROMBERG J,TAO T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information[J].IEEE Transaction on Information Theory,,2006,,52(2):489-509.
[4] DONOHO D,TSAIG Y.Extensions of compressed sensing[J]. Signal Processing,,2006,,86(3):533-548.
[5] DEVORE R.Deterministic constructions of compressed sensing matrices[J].Journal of Complexity,2007,,23(4-6):918-925.
[6] CANDES E,,TAO T.Near optimal signal recovery from random projections:universal encoding strategies[J].IEEE Transactions on Information Theory,2006,,52(12):5406-5425.
[7] RAUHUT H.Circulant and toeplitz matrices in compressed sensing[J].In Processing SPARS'09,,2009,2(13):1124-1132.
[8] 李浩.用于壓縮感知的確定性測量矩陣研究[D].北京:北京交通大學,,2011.
[9] CANDES E.The restricted isometry property and its implications for compressed sensing[J].C.R.Math.Acad.Sci.Paris,,2008,346(9-10):589-592.
[10] TROPP J,,GILBERT A.Signal recovery from partial infor-mation via orthogonal matching pursuit[EB/OL].(2005-04). [2012-11-22].http://www.personal.umich.edu/_jtropp/papers/TG05-Signal-Recovery.pdf.

