0 引言

    傳統(tǒng)A/D采用香農(nóng)-奈奎斯特采樣理論,，采樣速率至少等于信號(hào)帶寬的兩倍才能無(wú)失真地恢復(fù),。香農(nóng)-奈奎斯特采樣理論是可以重構(gòu)信號(hào)的充分條件，而不是必要條件,。理論上存在另外一種低于奈奎斯特速率的采樣方法,，通過(guò)這種方法也可以重構(gòu)恢復(fù)原信號(hào)。壓縮感知(Compressed Sensing,，CS)^[1-2]就是這樣一種革命性的采樣轉(zhuǎn)換技術(shù),，如果信號(hào)可以稀疏表示^[3-4]，壓縮感知能夠從少于香農(nóng)-奈奎斯特采樣的樣值中恢復(fù)信號(hào),。無(wú)線通信中的信號(hào)大多可以稀疏表示，例如超寬帶信號(hào)在時(shí)域中可以稀疏表示^[5-6],，跳頻信號(hào)在頻域可以稀疏表示^[7],。

    壓縮感知用于重構(gòu)可稀疏表示的信號(hào)，使其不失真地以奈奎斯特速率表示,。一些應(yīng)用有時(shí)候只關(guān)心傳輸信號(hào)中的信息,，而不需要重構(gòu)原信號(hào)。壓縮信號(hào)處理是一種直接處理壓縮后信號(hào)的方法,，它只是關(guān)心信號(hào)中的有用信息而不是重構(gòu)^[8],。區(qū)別于壓縮信號(hào)的恢復(fù)，本文對(duì)信號(hào)傳輸信道的估計(jì)和信號(hào)的檢測(cè)更感興趣,，文中主要解決二進(jìn)制偏移載波調(diào)制信號(hào)檢測(cè)問(wèn)題,。壓縮感知已經(jīng)應(yīng)用到擴(kuò)頻系統(tǒng)中偽隨機(jī)序列的捕獲^[9-10]，相關(guān)峰值在碼相位和頻偏組成的二維空間中是稀疏的,。CS可以用于降低GPS接收機(jī)的采樣頻率^[11],，但是其硬件實(shí)現(xiàn)較為復(fù)雜。文獻(xiàn)[12]指出的擴(kuò)頻接收機(jī)利用壓縮感知簡(jiǎn)化接收機(jī)設(shè)計(jì),，該文中對(duì)幾種接收機(jī)進(jìn)行了對(duì)比,，并分析了量化的影響,。應(yīng)用壓縮信號(hào)處理對(duì)直接序列擴(kuò)頻信號(hào)欠采樣解調(diào)^[13]，可以降低功耗和接收機(jī)的制造成本,，而且采用匹配濾波器比隨機(jī)解調(diào)器更為簡(jiǎn)單,。文獻(xiàn)[14]在頻率選擇信道上，構(gòu)建直接序列擴(kuò)頻通信系統(tǒng)的信道估計(jì)和符號(hào)檢測(cè)模型,，并分析了基于不同算法下的誤碼率性能,，表明采用CS輔助的SLSS-JCESD接收算法降低一半采樣速率，會(huì)損失1.2 dB的SNR,。

    現(xiàn)代GPS,、Galileo、北斗等導(dǎo)航衛(wèi)星系統(tǒng)中,，都啟用了二進(jìn)制偏移載波(Binary Offset Carrier,，BOC)調(diào)制技術(shù)。與傳統(tǒng)的BPSK相比,，BOC調(diào)制在載波調(diào)制之前增加了一個(gè)副載波調(diào)制環(huán)節(jié),。副載波是基于正弦相位或者余弦相位的方波，這兩種分別記為BOC_sin(Kn,，n)和BOC_cos(Kn,，n)，其中K表示副載波頻率與偽碼速率的比值,，n表示偽碼速率與f₀=1.023 MHz的比值,。與BPSK信號(hào)頻譜分布在載波處不同，BOC信號(hào)的頻譜主瓣分布在載頻±Knf₀處,，這使得BOC信號(hào)具有更寬的頻譜,，其帶寬通常記為副載波頻率與偽碼碼率之和的兩倍。針對(duì)BOC調(diào)制信號(hào)的特征,，本文中提出一種基于壓縮感知的BOC信號(hào)接收機(jī)和發(fā)射機(jī)模型,，并且采用壓縮信號(hào)處理的方式對(duì)接收到的BOC信號(hào)解調(diào)。收發(fā)機(jī)模型中匹配濾波器的使用,，降低了擴(kuò)頻通信系統(tǒng)的實(shí)現(xiàn)復(fù)雜度,。并且通過(guò)大量的仿真實(shí)驗(yàn)，對(duì)壓縮接收機(jī)和傳統(tǒng)接收的誤碼性能進(jìn)行分析對(duì)比,。

1 信號(hào)模型

    一個(gè)通用測(cè)量系統(tǒng)可以通過(guò)式(1)進(jìn)行描述：

其中,，x是N×1維被測(cè)量向量，Φ表示M×N維的測(cè)量矩陣,，M×1維向量y是測(cè)量值,。測(cè)量矩陣中每個(gè)行向量對(duì)x的觀測(cè)值，組成測(cè)量值向量y中的元素。測(cè)量可以簡(jiǎn)單地描述為通過(guò)測(cè)量值y和測(cè)量矩陣Φ,，求得未知值x,。

    目前，傳統(tǒng)采樣技術(shù)基于香農(nóng)-奈奎斯特采樣理論,。對(duì)于香農(nóng)-奈奎斯特測(cè)量系統(tǒng),，式(1)中，M=N,，并且?椎是N×N維的單位矩陣,。香農(nóng)-奈奎斯特采樣理論揭示了這種測(cè)量系統(tǒng)可以無(wú)失真恢復(fù)被測(cè)量值的條件。

    式(1)中當(dāng)M>N時(shí),，即得到的測(cè)量值數(shù)量多于未知被測(cè)量個(gè)數(shù),，與M=N類(lèi)似，可以唯一地求解出被測(cè)量值,。

    下面考慮式(1)中M<N的情況,。如果不增加任何條件，方程有無(wú)數(shù)多個(gè)解,，不能唯一地確定被測(cè)量值,。但是，如果被測(cè)量信號(hào)x是稀疏的,，則可以通過(guò)算法重構(gòu)被測(cè)量信號(hào),，即壓縮感知。

1.1 發(fā)射機(jī)模型

    帶通信號(hào)可以用其低通等效進(jìn)行表示,，即可以用處理低通等效信號(hào)代替處理帶通信號(hào),，這樣就減少了對(duì)信號(hào)進(jìn)行分析和仿真的復(fù)雜度。BOC基帶信號(hào)的生成可以分離為兩部分：基于BPSK基帶信號(hào)的擴(kuò)頻調(diào)制,、基于余弦或正弦相位的方波副載波調(diào)制,，如圖1所示。

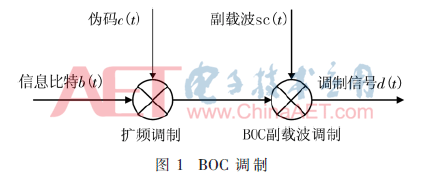
    在發(fā)射機(jī)和接收機(jī)中,，假設(shè)一次處理一個(gè)符號(hào)，該符號(hào)中包含一個(gè)或多個(gè)信息比特,，即向量b∈{±1}^L×1是傳輸?shù)囊粋€(gè)符號(hào),，每個(gè)符號(hào)由L比特?cái)?shù)據(jù)組成。定義偽隨機(jī)序列向量為c∈{±1}^C×1,，其中包含C個(gè)碼片,。上述兩個(gè)向量是圖1中b(t)和c(t)離散表達(dá)。如果定義T_b和T_c分別表示數(shù)據(jù)信息周期和碼寬,，則有LT_b=CT_c,，即一個(gè)符號(hào)周期中含有整數(shù)個(gè)偽碼周期。BOC_sin(Kn，n)基帶信號(hào)中的一個(gè)符號(hào)可以通過(guò)式(2)表示：

其中,，Ψ是由偽隨機(jī)序列組成的字典,，它的每一列都是一個(gè)可能傳輸?shù)臄U(kuò)頻調(diào)制信號(hào)；a∈{0,，1}^M×1是稀疏向量,，僅有一個(gè)值不等于零，用于選擇從字典中選擇要發(fā)送的偽隨機(jī)序列,。向量a的稀疏度決定了可以采用壓縮感知的方法對(duì)BOC信號(hào)進(jìn)行解調(diào),。

1.2 BOC壓縮信號(hào)處理接收機(jī)原理

    信號(hào)在傳輸?shù)倪^(guò)程中會(huì)受到噪聲的干擾，接收機(jī)接收到的信號(hào)通?？梢悦枋鰹?

其中,，n(t)是加性高斯白噪聲,。接收信號(hào)的匹配濾波接收機(jī)結(jié)構(gòu)如圖2所示^[17],，接收信號(hào)先進(jìn)行匹配濾波，然后以偽碼速率進(jìn)行采樣,，最后進(jìn)行解擴(kuò),。

    假設(shè)信號(hào)在接收機(jī)端已經(jīng)完全同步,，接收信號(hào)中一個(gè)符號(hào)的接收采樣過(guò)程可以通過(guò)式(6)表示：

    基于硬件壓縮采樣結(jié)構(gòu)的隨機(jī)解調(diào)器中，接收信號(hào)首先需要與偽隨機(jī)序列相乘,，然后通過(guò)低通濾波^[4],。BOC信號(hào)在發(fā)射端已經(jīng)通過(guò)偽隨機(jī)序列進(jìn)行頻譜擴(kuò)展，因而在接收端偽隨機(jī)碼產(chǎn)生器可以省略,。BOC信號(hào)的調(diào)制過(guò)程中,，使用副載波波形作為脈沖成型波形，因此采樣之前的匹配濾波器需要做相應(yīng)的修改,?；谟布嚎s采樣的BOC信號(hào)接收欠采樣過(guò)程為：

其中，θ_i(t)=sc(t-iT_c),，0≤t<CT_c,，是匹配濾波器。κ=I/L∈(0,，1]是壓縮感知結(jié)構(gòu)中的欠采樣因子,，當(dāng)κ=1時(shí)沒(méi)有進(jìn)行壓縮，κ越小得到的采樣值數(shù)量相對(duì)于奈奎斯特采樣值的個(gè)數(shù)越少,。Θ=[θ₀(t)  θ₁(t)  …  θ_C-1(t)]^T是測(cè)量矩陣,，經(jīng)過(guò)測(cè)量采樣每比特信息得到I=Cκ個(gè)樣值。

    在接收端,，本文的目的是解調(diào)出a,，因而不需要重構(gòu)出壓縮感知的原始信號(hào)b(t)。可以通過(guò)壓縮信號(hào)處理的方法^[8],，在壓縮域直接對(duì)壓縮信號(hào)進(jìn)行處理解調(diào)出信息比特,。通過(guò)壓縮信號(hào)處理的方法對(duì)信號(hào)解調(diào)減小計(jì)算復(fù)雜度，省去了信號(hào)重構(gòu)的過(guò)程,。

2 仿真實(shí)驗(yàn)

    為了描述基于壓縮信號(hào)處理的接收機(jī)性能,，分別采用奈奎斯特采樣和壓縮感知硬件采樣對(duì)BOC信號(hào)接收解調(diào)，并比較在高斯白噪聲信道下各自的誤碼率性能,。文中僅在理想的情況下對(duì)BOC解調(diào)算法進(jìn)行分析,，不考慮載波頻偏的影響，并且認(rèn)為信號(hào)已經(jīng)同步,。實(shí)際應(yīng)用中,，載波的剝離可以通過(guò)載波跟蹤算法完成，碼字的同步亦可由延遲鎖定環(huán)確定,。

    為方便且不失一般性,，仿真中采用BOC（1，1）信號(hào),，偽隨機(jī)碼周期中含有32個(gè)碼片,，每比特信息用一個(gè)周期的32碼片進(jìn)行擴(kuò)頻。仿真采用蒙特卡羅算法,，設(shè)置錯(cuò)誤信息比特門(mén)限為100,，在相同的Eb/N0的情況下對(duì)比兩種解調(diào)方法的誤碼率。仿真結(jié)果如圖3所示,，在壓縮率κ=0.5的情況下,，為得到同樣的誤碼性能(誤碼率10^-5)，使用壓縮信號(hào)處理解調(diào)BOC信號(hào)比采用經(jīng)典方法解調(diào)BOC信號(hào)需要高出3 dB左右的信噪比,。但是采樣速率降低了1/2,，后續(xù)處理的計(jì)算量減少了一半。壓縮信號(hào)處理方法中,，解調(diào)損失的信噪比是由噪聲折疊引入^[18],。

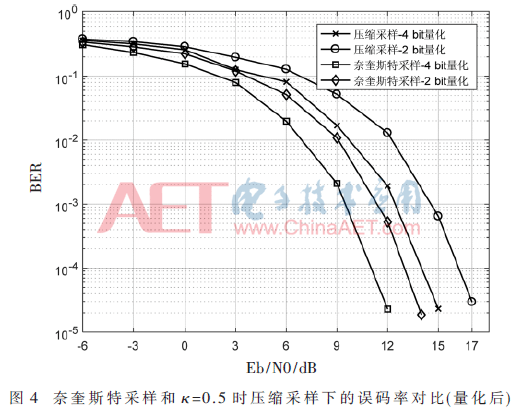
    采樣后需要量化，量化分辨率影響誤碼性能,，如圖4所示,。為了評(píng)定壓縮采樣和奈奎斯特采樣量化后對(duì)誤碼性能的影響，在相同的量化總比特?cái)?shù)下對(duì)其進(jìn)行對(duì)比,。也就是說(shuō)，奈奎斯特采樣速率下2 bit量化和1/2壓縮采樣下4 bit量化具有相同的量化總比特?cái)?shù),。對(duì)比這兩種情況,，同樣達(dá)到誤碼率10^-5，壓縮采樣所需的信噪比僅僅比奈奎斯特采樣多1 dB。在采樣率受限的情況下,，可以通過(guò)增加量化分辨率改善誤比特性能,。

3 結(jié)論

    本文應(yīng)用壓縮感知的方法產(chǎn)生BOC信號(hào)，副載波波形為其成型波形,，并采用壓縮信號(hào)處理對(duì)BOC信號(hào)解調(diào),。解調(diào)算法不同于隨機(jī)解調(diào)器，接收端不需要與隨機(jī)序列相乘,，實(shí)現(xiàn)簡(jiǎn)單,。這種基于壓縮信號(hào)處理的BOC信號(hào)解調(diào)方案所需要的采樣速率低于奈奎斯特采樣速率，有利于降低系統(tǒng)功耗和器件成本,。壓縮信號(hào)處理可以解決目前信號(hào)處理的瓶頸,，即越來(lái)越高的采樣頻率、大量數(shù)據(jù)的存儲(chǔ)處理和分析,?？梢韵胂髩嚎s信號(hào)處理有著廣泛的應(yīng)用空間，特別是對(duì)高帶寬的擴(kuò)頻信號(hào),，壓縮信號(hào)處理有天然的吸引力,。

參考文獻(xiàn)

[1] CANDES E J，ROMBERG J,，TAO T.Stable signal recovery from incomplete and inaccurate measurements[J].Communications on Pure and Applied Mathematics,，2006，59(8)：1207-1306.

[2] DONOHO D L.Compressed sensing[J].IEEE Transaction on Information Theory,，2006,，52(4)：1289-1306.

[3] TROPP J A，LASKA J N,，DUARTE M T,，et al.Beyond Nyquist：efficient sampling of sparse bandlimited signals[J].IEEE Transaction on Information Theory，2010,，56(1)：520-544.

[4] 翁天陽(yáng),，莊宇，于瑋,，等.基于HPS和FPGA的圖像壓縮感知編解碼系統(tǒng)[J].電子技術(shù)應(yīng)用,，2017，43(5)：90-93.

[5] OKA A,，LAMPE L.A compressed sensing receiver for UWB impulse radio in bursty applications like wireless sensor network[J].Physical Communication,，2009，2(4)：248-264.

[6] PAREDES J L,，ARCE G R,，WANG Z.Ultra-wideband compressed sensing：channel estimation[J].IEEE Journal of Selected Topics in Signal Processing,，2007，1(3)：383-395.

[7] LASKA J,，KIROLOS S,，MASSOUD Y，et al.Random sampling for analog-to-information conversion of wideband signals[C].IEEE DCAS Workshop,，Dallas,，TX，USA,，2006：119-122.

[8] DAVENPORT M A,，BOUFOUNOS P T，WAKIN M B,，et al.Signal processing with compressive measurements[J].IEEE Journal of Selected Topics in Signal Processing,，2010，4(2)：445-460.

[9] AGGARWAL V.Enhanced CDMA communications using compressed-sensing reconstruction methods[C].47th Annual Allerton Conference on Communication,，Control,，and Computing，Illinois：UIUC,，2009：1211-1215.

[10] 鄭昆,，張曉林.一種改進(jìn)的BOC(kn，n)信號(hào)無(wú)模糊跟蹤方法[J].電子技術(shù)應(yīng)用,，2018,，44(9)：116-120.

[11] LI X.GPS signal acquisition via compressive multichannel sampling[J].Physical Communication，2012,，5(2)：173-184.

[12] FYHN K,，JENSEN T L，LARSEN T,，et al.Compressive sensing for spread spectrum receivers[J].IEEE Transactions on Wireless Communications,，2013，12(5)：2334-2343.

[13] FYHN K.Demodulating subsampled direct sequence spread spectrum signals suing compressive signal processing[C].20th European Signal Processing Conference,，Bucharest,，Romania：EUSIPCO，2012：2556-2560.

[14] Wang Shuai,，An Jiangping,，Ren Yanyang，et al.Compressed receiver for multipath DSSS signals[J].IEEE Communcations Letters,，2014,，18(8)：1359-1362.

[15] BETZ J.Binary offset carrier modulation for radionavigation[J].Navigation：Journal of the Institute of Navigation，2001-2002,，48(4)：227-246.

[16] PRATT A,，OWEN J.BOC modulation waveforms[C].ION GPS/GNSS,，Portland，OR：ION,，2003：1044-1057.

[17] PROAKIS J G，SALEHI M.Digital communications(5th Edition)[M].New York：McGraw-Hill,，2008.

[18] METZLER C A,，MALEKI A，BARANIUK R G.From denoising to compressed sensing[J].IEEE Transactions on Information Theory,，2016,，62(9)：5117-5144.

作者信息:

宋  朋1，何國(guó)棟2

(1.中國(guó)電子科技集團(tuán)公司第五十八研究所,，江蘇 南京210000,；

2.安徽師范大學(xué) 物理與電子信息學(xué)院，安徽 蕪湖241003)