摘  要： 由于蓄電池機(jī)理復(fù)雜，蓄電池的溫度具有明顯的非線性,、滯后性和模型不確定性,，采用BP神經(jīng)網(wǎng)絡(luò)對(duì)蓄電池溫度進(jìn)行仿真研究，建立網(wǎng)絡(luò)模型,，反映蓄電池溫度變化趨勢(shì),。
關(guān)鍵詞： BP算法；神經(jīng)網(wǎng)絡(luò),；蓄電池,；溫度；模型

    蓄電池的溫度變化是一個(gè)復(fù)雜的,、多變量相互影響的過(guò)程,，不僅受環(huán)境因素影響，還與充放電時(shí)間,、充放電電流,、內(nèi)阻大小、使用壽命等有關(guān),。蓄電池溫度與各因素之間存在非線性關(guān)系,，很難用數(shù)學(xué)解析的方式建立準(zhǔn)確的模型[1-2],。
    蓄電池的溫度值直接影響到電池容量，可以根據(jù)蓄電池的使用壽命,、工作狀態(tài),、運(yùn)行時(shí)間估算出蓄電池的溫度和電池剩余容量，為蓄電池做出可行的預(yù)判,，因此掌握蓄電池的溫度值是很重要的,。本文采用神經(jīng)網(wǎng)絡(luò)建模的方法模擬蓄電池溫度，為使用者提供比較準(zhǔn)確的參考[3],。
    根據(jù)蓄電池物理特性的要求,，電池的充電和放電不能同時(shí)進(jìn)行，否則會(huì)損害電池性能,，造成不可挽回的損壞,。電池充電時(shí)溫度值變化呈現(xiàn)一定的趨勢(shì)，前期大電流充電制,，由于充電電流很大,，蓄電池內(nèi)阻產(chǎn)生的熱量加上電池電化學(xué)反應(yīng)產(chǎn)生的熱量，使溫度急劇升高,；隨著充電時(shí)間的增加,，充電電流變小，內(nèi)阻產(chǎn)生的熱量隨之減少,，蓄電池與外部環(huán)境交換熱量的增加,，致使蓄電池溫度出現(xiàn)下降的現(xiàn)象。蓄電池放電時(shí)溫度變化呈現(xiàn)不規(guī)則趨勢(shì),，這主要與蓄電池的工作狀態(tài),、放電制要求有關(guān)，當(dāng)采用大電流放電制時(shí),，蓄電池內(nèi)阻產(chǎn)生的熱量會(huì)大于電池電化學(xué)反應(yīng)吸收的熱量,，電池溫度持續(xù)上升；當(dāng)蓄電池采用的工況改變,，放電制電流減小時(shí),，電池電化學(xué)反應(yīng)的吸熱會(huì)大于內(nèi)阻產(chǎn)生的熱量，電池溫度又會(huì)下降[4],。
    由此可見(jiàn),，蓄電池的充放電過(guò)程溫度變化極其不規(guī)則，溫度值的改變受各種因素的影響,，要想建立準(zhǔn)確的數(shù)學(xué)模型具有很大的困難,，因此本文以實(shí)驗(yàn)數(shù)據(jù)為基礎(chǔ)，建立神經(jīng)網(wǎng)絡(luò)模型,，并進(jìn)行仿真研究,，時(shí)時(shí)了解蓄電池溫度情況,，為蓄電池的工作提供必要的信息。
1 前饋型神經(jīng)網(wǎng)絡(luò)模型
    前饋型網(wǎng)絡(luò)包含輸入層,、隱含層和輸出層,。通常網(wǎng)絡(luò)有一個(gè)或多個(gè)隱含層，隱含層的神經(jīng)元數(shù)量由訓(xùn)練效果來(lái)確定,。輸入層可以看做是緩沖器,，沒(méi)有處理功能。隱含層的非線性傳遞函數(shù)神經(jīng)元可以學(xué)習(xí)輸入輸出之間的線性和非線性關(guān)系,，進(jìn)行權(quán)值處理,。輸出層的作用是拓寬網(wǎng)絡(luò)輸出。圖1所示為具有單隱含層的BP網(wǎng)絡(luò)模型,。

    在確定了神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)后,，通過(guò)輸入和輸出樣本集對(duì)網(wǎng)絡(luò)進(jìn)行訓(xùn)練，即對(duì)網(wǎng)絡(luò)的閾值和權(quán)值進(jìn)行學(xué)習(xí)和修正,，使網(wǎng)絡(luò)實(shí)現(xiàn)給定的輸入輸出映射關(guān)系。其學(xué)習(xí)分為兩個(gè)階段：
    （1）輸入已知的學(xué)習(xí)樣本,，通過(guò)設(shè)置網(wǎng)絡(luò)結(jié)構(gòu)和前一次迭代的權(quán)值和閾值,，從網(wǎng)絡(luò)的第一層向后計(jì)算各神經(jīng)元的輸出；
    （2）對(duì)權(quán)值和閾值進(jìn)行修改,。從最后一層向前計(jì)算各權(quán)值和閾值對(duì)總誤差的影響（梯度）,，據(jù)此對(duì)各權(quán)值和閾值進(jìn)行修改。以上兩個(gè)過(guò)程反復(fù)交替,，直到達(dá)到收斂為止,。
2 Levernberg-Marquart算法
    標(biāo)準(zhǔn)的BP算法是一種梯度下降的學(xué)習(xí)算法，其權(quán)值的修正是沿著誤差性能函數(shù)梯度的反方向進(jìn)行的,，其主要不足是訓(xùn)練時(shí)間較長(zhǎng),。相應(yīng)的有許多加速收斂技術(shù)，如變量BP算法,、變梯度算法,、擬牛頓算法、LM算法等,。
    通常對(duì)于權(quán)值數(shù)較少的用于逼近函數(shù)的神經(jīng)網(wǎng)絡(luò),，LM算法的收斂速度較快。如果要求的精度比較高,，則該算法的優(yōu)點(diǎn)尤其突出,，采用LM算法可以獲得比其他算法更小的均方誤差。其具體計(jì)算步驟如下：
    （1）將所有輸入提交網(wǎng)絡(luò)并計(jì)算相應(yīng)的網(wǎng)絡(luò)輸出和誤差,；
    （2）計(jì)算雅克比矩陣,；
    （3）求取誤差?駐xk,；
    （4）用xk+?駐xk重復(fù)計(jì)算平方誤差之和，當(dāng)平方誤差之和小于某個(gè)目標(biāo)值時(shí),，認(rèn)為算法收斂,。
3 蓄電池充電模型
    蓄電池采用4階段充電制，當(dāng)?shù)竭_(dá)過(guò)渡電壓時(shí)本階段充電電流就轉(zhuǎn)為下一階段的充電電流,，順序?yàn)? 400 A—1 200 A—600 A—300 A[5],。
    根據(jù)前面的分析確定神經(jīng)網(wǎng)絡(luò)采用三層模型結(jié)構(gòu)，輸入層3個(gè)輸入量：充電時(shí)間,、充電制和電解液密度,；輸出層1個(gè)輸出量：蓄電池溫度；隱含層的神經(jīng)元數(shù)量定為5個(gè)（后續(xù)網(wǎng)絡(luò)建立,，訓(xùn)練數(shù)據(jù)時(shí),，發(fā)現(xiàn)選用5個(gè)中間節(jié)點(diǎn)的隱含層，網(wǎng)絡(luò)訓(xùn)練的效果最佳,，數(shù)據(jù)擬合程度最高）,。表1為訓(xùn)練網(wǎng)絡(luò)用的部分實(shí)驗(yàn)數(shù)據(jù)；表2為充電時(shí)電解液密度的變化數(shù)據(jù),。

    蓄電池的電解液密度變化與溫度,、放電歷史互為影響，但影響效果有限,，同一時(shí)刻不同組的密度數(shù)據(jù)僅相差0.02 g/cm3,。
    圖2所示為BP神經(jīng)網(wǎng)絡(luò)模型模擬的充電溫度變化曲線圖。圖3為充電仿真步數(shù)精度曲線圖,，從圖中可以看出訓(xùn)練精度可達(dá)10-3,。圖4為預(yù)測(cè)數(shù)據(jù)擬合圖，從中可以看出,，預(yù)測(cè)數(shù)據(jù)與測(cè)量值的誤差不超過(guò)1 ℃,，原因是用于訓(xùn)練網(wǎng)絡(luò)的實(shí)驗(yàn)數(shù)據(jù)量比較小，造成了局部時(shí)間內(nèi)誤差偏大,，如果采用大量的實(shí)驗(yàn)數(shù)據(jù)進(jìn)行仿真,，則能得到更理想的效果。

4 蓄電池放電模型
    蓄電池溫度并非隨時(shí)間的增加而上升,，在長(zhǎng)時(shí)放電的情況下(50 h和20 h放電制),，蓄電池溫度是逐步降低的，而在短時(shí)放電時(shí)(5 h,、1 h以及0.5 h放電制),，蓄電池溫度是逐漸上升的[5]。圖5和圖6分別為長(zhǎng)時(shí)和短時(shí)放電情況下電解液溫度變化曲線。

    蓄電池內(nèi)阻在放電過(guò)程中隨著放電電流,、放電時(shí)間而變化,。在內(nèi)阻變化不是很大的情況下，內(nèi)阻產(chǎn)生的熱量(Q=I2R)主要取決于放電電流,。
    表3所示為在不同放電制下蓄電池內(nèi)阻隨放電時(shí)間的變化情況,，從中可以看出，當(dāng)大電流放電時(shí),，蓄電池的內(nèi)阻是逐漸減小的,；而當(dāng)小電流放電時(shí)，長(zhǎng)時(shí)間放電使蓄電池電動(dòng)勢(shì)降低,，電池內(nèi)阻逐漸增大,。
    蓄電池長(zhǎng)時(shí)放電時(shí)，電化學(xué)吸收的熱量大于內(nèi)阻放出的熱量,，以至蓄電池的溫度保持下降,，短時(shí)放電時(shí)電化學(xué)吸收的熱量小于內(nèi)阻放出的熱量，造成蓄電池的溫度變化與長(zhǎng)時(shí)放電時(shí)正好相反,。蓄電池放電溫度模型輸入層采用3個(gè)輸入量：放電制,、放電時(shí)間和電解液內(nèi)阻；輸出層采用1個(gè)變量：蓄電池溫度,；隱含層選用5個(gè)元素作為中間節(jié)點(diǎn),。
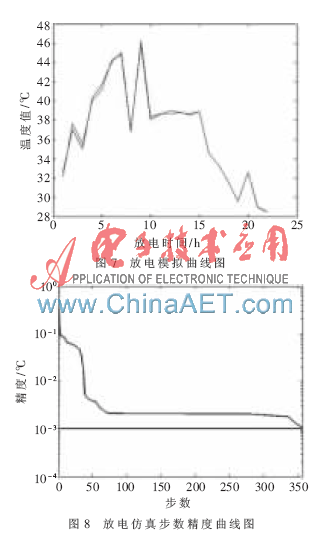
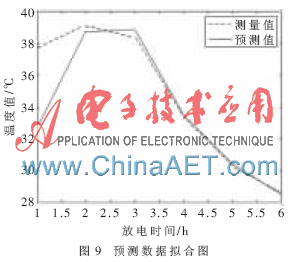
    圖7為放電模擬曲線圖，圖8為放電仿真步數(shù)精度曲線圖,，從圖7和圖8可以看出網(wǎng)絡(luò)模擬的精度很高。圖9是預(yù)測(cè)數(shù)據(jù)擬合圖,，從中可以看到,，初始時(shí)刻溫度預(yù)測(cè)數(shù)據(jù)與測(cè)量值的誤差很大，造成這種情況的主要原因是開(kāi)始時(shí)刻溫度值變化大,，變化速度快,，實(shí)驗(yàn)數(shù)據(jù)量比較小。

    本文根據(jù)蓄電池的化學(xué)特性,，影響蓄電池溫度變化的因素,，提出用BP神經(jīng)網(wǎng)絡(luò)建立蓄電池充放電時(shí)的溫度模型。建立模型的預(yù)測(cè)值與實(shí)際測(cè)量值擬合程度較高,，對(duì)時(shí)刻掌握蓄電池性能,、溫度數(shù)據(jù)等起到很大的輔助作用。
參考文獻(xiàn)
[1] 黃曉輝,，黃聲華,，萬(wàn)山明.基于DSP的潛艇蓄電池分級(jí)恒流充電控制系統(tǒng)研究[J].船電技術(shù)，2007,，27(6)：329-333.
[2] 畢恩利,，朱華兵.基于某型潛艇蓄電池組巡檢系統(tǒng)設(shè)計(jì)[J].機(jī)電工程技術(shù),，2007，36(3)：28-30.
[3] 許亦峰,，張榮昌.常規(guī)潛艇水下電量消耗建模與仿真[J].青島大學(xué)學(xué)報(bào),，2008，21(2)：43-46.
[4] 馬守軍,，莊亞平,，陳新傳.潛艇蓄電池建模策略分析[J].船電技術(shù)，2004,，24(4)：23-25.
[5] 徐魯杰,，劉鎮(zhèn).潛艇用新型鉛酸蓄電池萬(wàn)用放電模型研究[J].武漢理工大學(xué)學(xué)報(bào)，2009,，33(1)：177-179.