《電子技術(shù)應(yīng)用》
您所在的位置：首頁 > 通信與網(wǎng)絡(luò) > 設(shè)計(jì)應(yīng)用 > S模式數(shù)據(jù)鏈自適應(yīng)航跡跟蹤濾波器設(shè)計(jì)
S模式數(shù)據(jù)鏈自適應(yīng)航跡跟蹤濾波器設(shè)計(jì)
來源：電子技術(shù)應(yīng)用2014年第4期
方 正1, 2, 3,， 仇啟明2,， 丁勇飛2,， 龔 誠2
(1. 航空電子系統(tǒng)綜合技術(shù)重點(diǎn)實(shí)驗(yàn)室,，上海 200223,； 2. 中國航空無線電電子研究所,，上海
摘要： 如何設(shè)計(jì)和實(shí)現(xiàn)適合空管系統(tǒng)使用的自適應(yīng)濾波器成為了實(shí)現(xiàn)航跡濾波和目標(biāo)跟蹤的關(guān)鍵,。首先對飛行器的三維空間運(yùn)動軌跡建?！袄窭嗜铡保↙agrange）三階級數(shù)展開，基于此設(shè)計(jì)了一種兼顧實(shí)時性和預(yù)測濾波效果的數(shù)據(jù)處理算法,，通過對該濾波器模型穩(wěn)定性,、初始狀態(tài)、收斂性,、濾波參數(shù)等的深入分析,，提出了一種基于“查表”策略的“殘差-新息”估計(jì)方法,，在保證收斂性的同時兼顧了收斂速度，一系列建模仿真和飛行試驗(yàn)均表明了所論述關(guān)鍵技術(shù)的有效性,。
中圖分類號： TN961
文獻(xiàn)標(biāo)識碼： A
文章編號： 0258-7998(2014)04-0099-04
The design of adaptive tracking filter applied in Mode-S data link
Fang Zheng1,2,3, Qiu Qiming2, Ding Yongfei2,， Gong Cheng2
1. Science and Technology on Avionics Integration Laboratory, Shanghai 200223, China;2. China National Aeronautical Radio Electronics Research Institute, Shanghai 200241, China;3. Shanghai Jiao Tong University, School of Electronic, Information and Electrical Engineering, Shanghai 200240, China
Abstract： How to design and implement the adaptive filter for air traffic control system has become the key to realize trace filtering and target tracking. This paper firstly models the 3D spatial trajectory of the aircraft by three order Lagrange expansion, and designs data processing algorithm considering both real-time and predictive filtering effect based on this model, and proposes one ′relics-innovation′ estimation method based on ′Looking Up Table′ strategy by thorough analysis of the stability, original state, convergence and filter parameters of the filter model, which ensures both reliability and speed of system convergence. The effectiveness of the key technology in this paper is demonstrated by a series of simulations and flight tests.
Key words : Mode-S data link; Lagrange series; relics-innovation

    在空中交通管制系統(tǒng)中，S模式數(shù)據(jù)鏈是空-空數(shù)據(jù)鏈和空-地?cái)?shù)據(jù)鏈的重要組成部分,，也是反映空中交通態(tài)勢,、保證飛行安全的一項(xiàng)重要手段。隨著國家在空管事業(yè)上的大力投入,，以及傳統(tǒng)的航管雷達(dá)體制[1]存在覆蓋范圍小及運(yùn)營成本高等諸多問題,，發(fā)展具有自主知識產(chǎn)權(quán)的S模式數(shù)據(jù)鏈技術(shù)[2](如圖1)成為目前和未來幾年中國內(nèi)各相關(guān)研究機(jī)構(gòu)的重要任務(wù)。而在該領(lǐng)域中,，自適應(yīng)濾波目標(biāo)跟蹤定位技術(shù)是關(guān)鍵,，該技術(shù)的合理運(yùn)用，有助于濾除目標(biāo)飛行器地理位置觀測信息中的觀測噪聲,，提高目標(biāo)飛行器的航跡穩(wěn)定度,，對于確保空中交通情景態(tài)勢的可靠性和準(zhǔn)確性起到重要作用,。

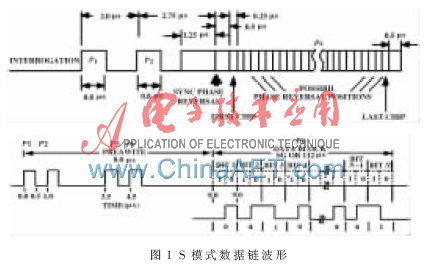
    為適應(yīng)實(shí)際應(yīng)用需求,，可靠性和實(shí)時性是行業(yè)內(nèi)對于該項(xiàng)技術(shù)的兩個核心要求，前者要求所采用的核心算法具有良好的魯棒性(robust)和收斂性(convergence),，后者則對算法的優(yōu)化及復(fù)雜度的降低提出了很高要求,。目前，國內(nèi)自適應(yīng)濾波目標(biāo)跟蹤定位技術(shù)在S模式領(lǐng)域的研究和實(shí)際應(yīng)用還處于起步階段,，而國外相關(guān)領(lǐng)域的研究和應(yīng)用目前主要集中在基于卡爾曼濾波的核心算法上,，雖然能夠達(dá)到較好的收斂特性和較小的殘余方差，但運(yùn)算復(fù)雜度較高,，其算法實(shí)現(xiàn)過程中需要進(jìn)行大量的矩陣運(yùn)算(即使采用行業(yè)內(nèi)普遍的近似算法,，算法復(fù)雜度也是很可觀的),，這無疑給實(shí)時性,、成本和功耗帶來很大挑戰(zhàn)。即使是基于α-β-γ核心算法的研究,，也主要集中在如何從殘差(relics)中提取“新息”(innovation)以及如何建模增益矩陣(Gain matrix)上,，對該算法本身的穩(wěn)定性、初始狀態(tài)和相關(guān)參數(shù)的選取與優(yōu)化未作深入考慮,，而這些方面對于飛行器安全是非常重要的,。
    本文技術(shù)探討的目標(biāo)有以下三點(diǎn)：
　(1) 設(shè)計(jì)一種適合空中交通管制系統(tǒng)的自適應(yīng)(航跡跟蹤)濾波器，解決當(dāng)前國內(nèi)相關(guān)技術(shù)領(lǐng)域普遍存在的實(shí)時性與設(shè)計(jì)復(fù)雜度之間的矛盾,；
   (2) 對飛行器的三維空間運(yùn)動軌跡建模“拉格朗日”(Lagrange)三階級數(shù)展開,，設(shè)計(jì)一種兼顧實(shí)時性和預(yù)測濾波效果的算法模型,，并對該濾波器模型的穩(wěn)定性、初始狀態(tài),、收斂性,、濾波參數(shù)等進(jìn)行深入分析；
   (3) 提出一種基于“查表”策略的“殘差-新息”估計(jì)方法,，在保證收斂性的同時兼顧了收斂速度,，“表”的維護(hù)更新就是SNR實(shí)時估計(jì)的過程，可根據(jù)樣值二階數(shù)學(xué)期望的無偏估計(jì)統(tǒng)計(jì)得出,。


求式(5)表征的系統(tǒng)傳遞函數(shù)的“全部復(fù)極點(diǎn)包含在單位圓內(nèi)”[6],。通常需要實(shí)時計(jì)算矩陣求逆和特征值，這將給工程應(yīng)用帶來較大困難,。以下給出工程應(yīng)用時的一種較為簡便的保證收斂性的處理方法,。

    計(jì)算信號與觀測噪聲的比值最為關(guān)鍵,根據(jù)Bernoulli大數(shù)定理對觀測噪聲進(jìn)行數(shù)值分析，從大量的觀測樣本中可以通過二階中心矩反映觀測噪聲強(qiáng)度,，再通過“查找表”(預(yù)置的q-SNR收斂性曲線,，可仿真獲得)的方法確定合適的自適應(yīng)參數(shù)，從而保證算法的收斂性,。
3 建模仿真
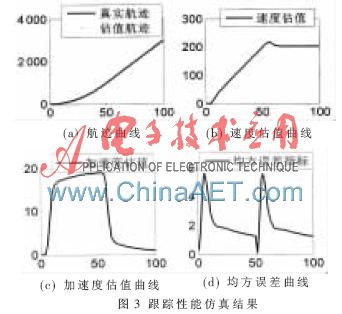
3.1 跟蹤性能仿真
    真實(shí)運(yùn)動航跡為二次曲線,，前半程勻加速運(yùn)動、后半程勻速運(yùn)動,。圖3仿真的是理想觀測環(huán)境(無觀測噪聲)中自適應(yīng)算法的跟蹤性能,。
    從圖3(a)中可以看出，航跡估計(jì)值和真實(shí)值重合,，圖3(b)和圖3(c)的速度估值曲線和加速度估值曲線則反映了飛機(jī)的運(yùn)動過程,，圖3(d)的均方誤差曲線顯示在初始時刻(由靜止到啟動)和由勻加速運(yùn)動轉(zhuǎn)為勻速運(yùn)動的時刻，會出現(xiàn)“沖擊”,，這與圖3(b)的速度估值曲線和圖3(c)的加速度估值曲線的分析結(jié)果是吻合的,。

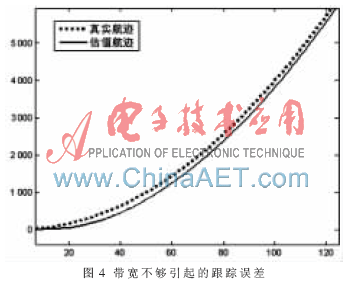
    減小q值，濾波器等效帶寬變小,，不能準(zhǔn)確跟蹤真實(shí)航跡,， 在大機(jī)動情況下存在跟蹤誤差， 仿真結(jié)果如圖4所示,。

 

 

3.2 濾波性能仿真
    真實(shí)運(yùn)動航跡為正弦曲線,，圖5仿真的是有噪環(huán)境下自適應(yīng)算法的濾波跟蹤結(jié)果，圖5(a)對比了觀測航跡和濾波跟蹤航跡,，圖5(b)對比了真實(shí)航跡和濾波跟蹤航跡,。仿真結(jié)果說明：通過選擇合適的濾波器帶寬，可以同時達(dá)到濾除觀測噪聲和跟蹤目標(biāo)機(jī)動的目的,。

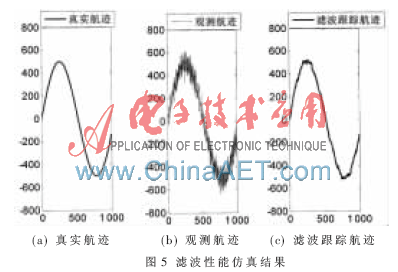
   上述仿真結(jié)果驗(yàn)證了以下兩個結(jié)論：
    (1) 自適應(yīng)航跡跟蹤濾波器的數(shù)學(xué)模型是三階拉格朗日級數(shù)展開,，因而在理想觀測環(huán)境中可以由任意估計(jì)初值無誤差地跟蹤機(jī)動目標(biāo)的真實(shí)二次運(yùn)動軌跡(勻加速運(yùn)動或者勻速運(yùn)動),。
    (2) 從時域角度看，q值影響跟蹤濾波的收斂性,，從頻域角度看,，q值影響濾波器帶寬，在不同噪聲強(qiáng)度的觀測環(huán)境下,，q值的選取是否合適直接影響到航跡濾波和跟蹤的效果,。
　在空中交通管制系統(tǒng)S模式數(shù)據(jù)鏈領(lǐng)域，國內(nèi)外當(dāng)前普遍采用的自適應(yīng)航跡濾波跟蹤技術(shù)主要是“基于Kalman濾波模型的MSE準(zhǔn)則算法”,，這也是FAA DO-181C,、DO-260A等適航標(biāo)準(zhǔn)推薦的信號處理方法。與之相比, 本文論述關(guān)鍵技術(shù)在以下幾個方面有其自身特點(diǎn)：
　(1) 實(shí)現(xiàn)復(fù)雜度方面：相對Kalman濾波模型,，本文采用的算法建模復(fù)雜度較低,，這是因?yàn)镵alman濾波模型在運(yùn)算過程中需要牽涉數(shù)次矩陣求逆，即使采用逼近簡化算法,，其運(yùn)算量也相當(dāng)可觀,，與之相比，采用濾波參數(shù)替代了 “增益矩陣”,，在實(shí)現(xiàn)復(fù)雜度,、運(yùn)算資源以及系統(tǒng)功耗等方面具備優(yōu)勢。
　(2) 收斂性方面：如果采用矩陣運(yùn)算求解Kalman濾波模型,則不牽涉收斂性問題(也不存在收斂時間),，如果采用傳統(tǒng)LMS方法[4]迭代“逼近”,，則同樣存在收斂性問題；本文提出的基于“查表”策略的“殘差-新息”估計(jì)方法,，在保證收斂性的同時兼顧了收斂速度,，與傳統(tǒng)LMS方法解算Kalman濾波模型相比，在保證收斂性和收斂速度方面具有優(yōu)勢,。
    本文論述的關(guān)鍵技術(shù)以本文第一作者參與和負(fù)責(zé)的某項(xiàng)目為背景,，是經(jīng)過了軍航體系使用鑒定的成熟技術(shù)，能夠在較低硬件處理平臺資源的需求下達(dá)到國外同類設(shè)備的性能,，同時降低了功耗和使用,、維護(hù)成本。隨著國家低空空域開放和在民用航空領(lǐng)域的大力投入,，本文論述的關(guān)鍵技術(shù)具有較為廣闊的應(yīng)用前景,。
參考文獻(xiàn)
[1] 李濤,，鐘志峰,，黃堅(jiān). 一種新的雷達(dá)動目標(biāo)檢測方法[J].微型機(jī)與應(yīng)用，2012,，31(17):72－74.
[2] SC-187, 2001 RTCA, Inc. Minimum Operational Performance Standards for Air Traffic Control Radar Beacon System/Mode Select(Atcbrs/Mode S)Airborne Equipment[S].USA:FAA,2001.
[3] SC-187, 2001 RTCA, Inc. Minimum Operational Performance Standards for 1 090 MHz Extended Squitter Automatic Dependent Surveillance-Broadcast(ADS-B) and Traffic  Information Services-Broadcast(TIS-B)[S].USA:FAA,2001.
[4] 陸光華,，彭學(xué)愚,，張林讓，等. 隨機(jī)信號處理[M]. 西安：西安電子科技大學(xué)出版社,，2002：48-57,62-76.
[5] 田增山,，刑培基，周非. 基于多尺度的EKF濾波融合定位跟蹤算法[J].電子技術(shù)與應(yīng)用,，2008,，34(10):120－123.
[6] 吳大正，楊林耀,，張永瑞. 信號與線性系統(tǒng)分析[M]. 第三版. 北京：高等教育出版社,，2002：305-317.

此內(nèi)容為AET網(wǎng)站原創(chuàng)，未經(jīng)授權(quán)禁止轉(zhuǎn)載,。