摘  要： 在高速設(shè)計(jì)中,，反射是其中的一個(gè)重要問題,。消除反射的最好辦法就是保證傳輸線的阻抗連續(xù)。分別從基于集總LC模型的理想無損傳輸線和基于集總RLGC模型的傳輸線的阻抗連續(xù)特性出發(fā),，通過歸納的方法得到了基于集總LC模型的理想無損傳輸線和基于集總RLGC模型的傳輸線的阻抗計(jì)算公式,。

　　關(guān)鍵詞： 反射；阻抗連續(xù)性；傳輸線,；集總模型

　　在電子系統(tǒng)中,，設(shè)備與設(shè)備之間，器件與器件之間都是通過導(dǎo)線相連的,。常見的傳輸線既包括平行雙導(dǎo)線,、同軸線和雙絞線等電纜傳輸線，也包括PCB板上微帶線和帶狀線,，如圖1所示,。這些導(dǎo)線有的很短，也有導(dǎo)線很長(zhǎng),，信號(hào)從信號(hào)源端傳到負(fù)載終端需要一定的時(shí)間,，這段時(shí)間對(duì)于低速電路系統(tǒng)可以忽略，但是對(duì)于高速電路系統(tǒng)會(huì)產(chǎn)生重要影響,，不能忽略,。對(duì)于這種必須考慮信號(hào)傳輸?shù)倪B接線，稱之為傳輸線,。由于信號(hào)在其上的傳輸需要時(shí)間,，因而常常也將傳輸線稱之為延遲線。

　　如果傳輸線的任何一處的橫截面都相同,，就稱為均勻傳輸線,，由于其阻抗可控，也稱為可控阻抗傳輸線,。如果傳輸線的橫截面不均勻,，就會(huì)出現(xiàn)阻抗不連續(xù)。阻抗不連續(xù)的后果就是高速信號(hào)在傳輸時(shí)出現(xiàn)電磁波的反射,，使信號(hào)波形嚴(yán)重畸變,，并且引起一些有害的干擾脈沖，影響整個(gè)系統(tǒng)的正常工作,。

　　通常阻抗定義為電壓與電流之比,。在傳輸線中，這個(gè)定義仍然有效,，傳輸線上任何一處的瞬時(shí)電壓與瞬時(shí)電流成正比,，流過傳輸線的瞬時(shí)電壓和瞬時(shí)電流的比值就稱為瞬態(tài)阻抗[1]。傳輸線的瞬態(tài)阻抗僅由傳輸線的橫截面和材料特性共同決定,，瞬態(tài)阻抗等于施加的電壓與流過器件的電流的比值,。特性阻抗是傳輸線的固有屬性，僅與材料特性,、介電常數(shù),、頻率有關(guān),，而與傳輸線的長(zhǎng)度無關(guān)。只要這3個(gè)參數(shù)不變,，瞬態(tài)阻抗就是一個(gè)常數(shù),。對(duì)于一個(gè)均勻的傳輸線，任何一處的瞬態(tài)阻抗都是相同的,，這樣一個(gè)恒定的瞬態(tài)阻抗就稱為傳輸線的特性阻抗,。

　　傳輸線是一個(gè)典型的分布參數(shù)系統(tǒng)，信號(hào)是以電磁波的形式在信號(hào)通道上傳輸,，信號(hào)通道是由電阻,、電容、電感及電導(dǎo)組成的復(fù)雜網(wǎng)絡(luò),。通常在電路分析中，使用集總參數(shù)系統(tǒng)來描述傳輸線,。集總參數(shù)系統(tǒng)就是把傳輸線的某一段分布參數(shù)（如阻抗,、容抗、感抗和電導(dǎo)）作為一個(gè)元件集中于空間的各個(gè)點(diǎn)上,，各點(diǎn)之間的信號(hào)是瞬間傳遞的,。本文將傳輸線分為基于集總LC模型的理想無損傳輸線和基于集總RLGC模型的實(shí)際傳輸線兩種情況來討論，得到各自狀況下的阻抗計(jì)算公式,。

　　1 基于集總LC模型的理想無損傳輸線阻抗求解

　　理想無損是一種理想狀態(tài),，在該狀態(tài)下，整個(gè)傳輸線可以用集總LC模型來描述,。首先從簡(jiǎn)單的單節(jié)理想傳輸線的集總LC模型出發(fā),，逐步過渡到兩節(jié)，甚至n節(jié),，最后推廣到無窮節(jié)集總LC模型,，得到理想狀況下的阻抗計(jì)算公式。

　　1.1 單節(jié)理想傳輸線集總LC模型

　　單節(jié)理想傳輸線集總LC電路模型如圖2所示[2],。整個(gè)傳輸線由分布電感L和分布電容C及特性阻抗Z0組成,。

　　根據(jù)阻抗連續(xù)特性的要求，必然得到A的阻抗ZA和特性阻抗Z0相等,，根據(jù)這個(gè)條件得到下列方程：

　　ZA=//（j?棕C+Z0）=Z0（1）

　　求解方程可以得到特性阻抗Z0：

　　Z0=-j（2）

　　1.2 兩節(jié)理想傳輸線集總LC模型

　　把整個(gè)傳輸線分成兩段,，組成兩節(jié)理想傳輸線集總LC模型。如圖3所示,，兩節(jié)理想傳輸線集總LC模型的組成和單節(jié)理想傳輸線集總LC模型類似,。不同的是它由兩個(gè)單節(jié)模型組成，而且其中的分布電感為L(zhǎng)/2,，分布電容為C/2,。

　　假設(shè)單節(jié)集總LC模型的阻抗公式依然成立,，將分布電感L/2和分布電容C/2帶入式（2）后得到：

　　Z0=-j（3）

　　將Z0的值代入后求得：

　　ZB=-j=Z0（4）

　　將ZB的值代入后求得：

　　ZA=-j=ZB=Z0（5）

　　通過式（5），得到了兩節(jié)集總LC模型的阻抗公式,。同時(shí)證明了前面假設(shè)的單節(jié)集總LC模型的阻抗公式在兩節(jié)模型中依然成立,。

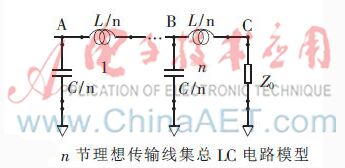
　　1.3 n節(jié)理想傳輸線集總LC模型

　　把整個(gè)傳輸線分成n段，組成n節(jié)理想傳輸線集總LC模型,，如圖所示,。n節(jié)理想傳輸線集總LC模型的組成和單節(jié)理想傳輸線集總LC模型類似。不同部分是它由n個(gè)單節(jié)模型組成,，而且其中的分布電感為L(zhǎng)/n,，分布電容為C/n。依然假設(shè)單節(jié)集總LC模型的阻抗公式成立,，根據(jù)單節(jié)集總LC模型的阻抗公式,，將分布電感L/n和分布電容C/n帶入式（2）后得到：

　　Z0=-j（6）

　　將Z0的值代入后求得：

　　ZB=-j=Z0（7）

　　逐級(jí)帶入后求得：

　　ZA=-j=…=ZB=Z0（8）

　　通過式（8），得到了n節(jié)集總LC模型下的阻抗公式,。同樣證明了前面假設(shè)的單節(jié)集總LC模型的阻抗公式在n節(jié)模型中依然成立,。因此可以將式（6）推廣到任意節(jié)集總LC模型。

　　用集總LC模型來模擬傳輸線,，模型的節(jié)數(shù)越多越能近似模擬理想傳輸線,，所以可以取LC節(jié)數(shù)為無窮大。根據(jù)上面的結(jié)論,，當(dāng)n→∞,，可以得到：

　　就是得到的理想狀態(tài)下傳輸線的阻抗計(jì)算公式。當(dāng)n→∞,，可以得到一個(gè)簡(jiǎn)明的無窮節(jié)集總LC電路模型,，如圖5所示[3]。

　　2 基于集總RLGC模型的傳輸線阻抗求解

　　實(shí)際的傳輸線一般用集總RLGC模型來描述,。首先從簡(jiǎn)單的單節(jié)集總RLGC模型出發(fā),，逐步過渡到兩節(jié)，甚至n節(jié),、無窮節(jié)集總RLGC模型,，得到實(shí)際狀況下的傳輸線的阻抗計(jì)算公式。

　　2.1 單節(jié)傳輸線集總RLGC模型

　　單節(jié)傳輸線集總RLGC電路模型如圖6所示[4],。整個(gè)傳輸線由分布電感L,、分布電阻R、分布電導(dǎo)G和分布電容C及特性阻抗Z0組成,。

　　根據(jù)傳輸線阻抗連續(xù)特性的要求,，必然得到A的阻抗ZA和特性阻抗Z0相等，根據(jù)這個(gè)條件得到下列方程：

　　ZA=//（R+j?棕C+Z0）=Z0（10）

　　求解方程可以得到特性阻抗Z0：

　　Z0=zB+ZA（11）

　　2.2 兩節(jié)傳輸線集總RLGC模型

　　把整個(gè)傳輸線分成兩段,，組成兩節(jié)傳輸線集總RLGC模型,。兩節(jié)傳輸線集總RLGC模型的組成和單節(jié)傳輸線集總RLGC模型類似,。不同的是它由兩個(gè)單節(jié)模型組成，而且其中的分布電感為L(zhǎng)/2,，分布電阻為R/2,，分布電導(dǎo)為G/2，分布電容為C/2,。

　　假設(shè)單節(jié)集總RLGC模型的阻抗公式依然成立,，將分布電感L/2、分布電阻R/2,、分布電導(dǎo)G/2和分布電容C/2帶入式（11）后得到：

　　Z0=L/2+ZB（12）

　　將Z0的值代入后求得：

　　ZB==Z0（13）

　　將ZB的值代入后求得：

　　ZA==ZB=Z0（14）

　　通過式（14）,，得到了兩節(jié)集總RLGC模型下阻抗公式。同時(shí)證明了前面假設(shè)的單節(jié)集總RLGC模型的阻抗公式在兩節(jié)模型中依然成立,。

　　2.3 n節(jié)傳輸線集總RLGC模型

　　把整個(gè)傳輸線分成n段,，組成n節(jié)傳輸線集總RLGC模型。n節(jié)傳輸線集總RLGC模型的組成和單節(jié)傳輸線集總RLGC模型類似,。不同部分是它由n個(gè)單節(jié)模型組成,，而且其中的分布電感為L(zhǎng)/n，分布電阻為R/n,，分布電導(dǎo)為G/n，分布電容為C/n,。依然假設(shè)單節(jié)集總RLGC模型的阻抗公式成立,，根據(jù)單節(jié)集總RLGC模型的阻抗公式，將分布電感L/n,、分布電阻R/n,、分布電導(dǎo)G/n和分布電容C/n

    到了n節(jié)集總RLGC模型下的阻抗公式。同樣證明了前面假設(shè)的單節(jié)集總RLGC模型的阻抗公式在n節(jié)模型中依然成立,。通過上述的歸納證明,，可以推廣到任意節(jié)集總RLGC模型。

　　同樣用集總RLGC模型來模擬傳輸線,，模型的節(jié)數(shù)越多越能近似模擬理想傳輸線,，所以可以取RLGC節(jié)數(shù)為無窮大。根據(jù)上面的結(jié)論,，當(dāng)n→∞,，可以得到：

　  就是得到的實(shí)際狀況下的傳輸線阻抗計(jì)算公式[5]。當(dāng)n→∞,，可以得到一個(gè)簡(jiǎn)明的無窮節(jié)集總RLGC電路模型,，如圖所示。

　　通過上面的歸納證明,，從傳輸線阻抗連續(xù)特性方面得到了傳輸線在理想狀況下和實(shí)際狀況下的阻抗計(jì)算公式,，也是從另一個(gè)角度用理論的方法驗(yàn)證阻抗計(jì)算公式的正確性,。對(duì)深入了解阻抗計(jì)算公式提供了理論基礎(chǔ)。從上面的模型也可以看出,，負(fù)載匹配是傳輸線阻抗連續(xù)的必要條件,，如果負(fù)載不匹配，會(huì)導(dǎo)致傳輸線阻抗出現(xiàn)不連續(xù),。

　　參考文獻(xiàn)

　　[1] ERIC BOGATIN著,，李玉山，李麗平譯.信號(hào)完整性分析[M].北京：電子工業(yè)出版社,，2005.

　　[2] JOHNSON H,， GRAHAM M. High speed digital design[M]. New Jersey： Prentice Hall PTR， 1993.

　　[3] JOHNSON H. High speed signal propagation[M]. New Jersey： Prentice Hall PTR,，2003.

　　[4] 陳偉,，黃秋元，周鵬.高速電路信號(hào)完整性分析與設(shè)計(jì)[M].北京：電子工業(yè)出版社,，2009.

　　[5] 梁昌紅,，王新穩(wěn)，李延平,，等.微波技術(shù)與天線[M].北京：電子工業(yè)出版社,，2011.