摘  要： 提出了一種改進的多群協(xié)作粒子群優(yōu)化算法,，該算法整個種群采用主從模式,，分為一個主群和多個從群，多個從群粒子統(tǒng)一地進行初始化操作,，從而避免了多個粒子群重復搜索現(xiàn)象,。同時，算法采取了一種擾動策略,，即當前全局最優(yōu)解在擾動因子的迭代周期內(nèi)保持不變時,，就重置粒子的速度,，迫使粒子群擺脫局部極小。該算法不僅增加了種群的多樣性,，擴大了搜索范圍,，而且還改善整個種群易陷入局部極小值的缺陷。通過9個基準函數(shù)進行測試,，實驗結(jié)果表明,，IMCPSO與MCPSO算法相比具有明顯的優(yōu)越性。

　　關鍵詞： 多群協(xié)作,；粒子群優(yōu)化,；函數(shù)優(yōu)化

　　粒子群優(yōu)化PSO（Particle Swarm Optimization）算法，由KENNEDY J和EBERHART R C[1-2]于1995年提出,，成為智能計算領域的研究熱點之一,。PSO算法是一種模擬自然生物界鳥群或魚群行為的隨機智能優(yōu)化算法，其全局搜索能力較強,，對一些粒子進行迭代計算獲取全局最優(yōu)解,。PSO算法是一種模擬自然界鳥群或魚群行為的隨機智能優(yōu)化算法。不少學者們也研究了一些改進算法來改善PSO算法的性能和收斂速度,。牛奔[3]等基于種群共生關系提出了多群協(xié)作粒子群優(yōu)化MCPSO（Multi-swarm Cooperative Particle Swarm Optimizer）算法的兩種進化結(jié)構(gòu),。而ZHAO S Z等[4]在2011年提出了關于動態(tài)拓撲結(jié)構(gòu)的多粒子群協(xié)同優(yōu)化算法。KONSTANTINOS E P[5]提出了主-從模式的并行微型結(jié)構(gòu)的多粒子群協(xié)同優(yōu)化算法,。

　　但是這些多粒子群優(yōu)化算法可能存在重復搜索,，造成粒子數(shù)目的浪費，同時又在多維數(shù),、多峰值優(yōu)化函數(shù)存在算法求解精度低及收斂度差等不足,，為此本文提出一種改進的多群協(xié)作粒子群協(xié)同粒子群優(yōu)化（IMCPSO）算法。該算法對從群粒子采取統(tǒng)一初始化操作,，避免在搜索初期造成的重復搜索現(xiàn)象,。同時，引入粒子擾動策略,，即當粒子陷入局部極小值時能夠重新設置粒子速度,，強制粒子擺脫陷入局部極小值的可能。

　　實驗仿真結(jié)果表明,，IMCPSO算法比MCPSO和PSO算法在尋優(yōu)精度和收斂速度都有大幅度的提高，并且具有較強的魯棒性,。

1 基本粒子群優(yōu)化算法

　　基本PSO算法利用單個粒子間的協(xié)作和競爭來搜索優(yōu)化問題的最優(yōu)解,。算法起初通過隨機生成初始化種群粒子，其中每個粒子作為優(yōu)化問題的一個候選方案,，并由目標函數(shù)計算出粒子適應值,。種群粒子在搜索空間里運動，通過自身速度向量來判定其運動的方向和長度。每個粒子跟隨當前自身最優(yōu)位置和種群的最優(yōu)位置而運動,，最后經(jīng)過多次搜索得到優(yōu)化問題的最優(yōu)解,。

　　假設在D維搜索空間里，粒子搜索空間的上,、下界分別為xmax,、xmin。第i個粒子的位置和速度矢量分別為xi=（xi1,，xi2,，…，xiD）,，vi=（vi1,，vi2，…,，viD）,，其中xiD∈（xmax，xmin）,，d∈[1,，D]。Pi=（pi1,，pi2,，…，piD）表示為第i個粒子的當前最優(yōu)位置矢量,，Pg=（pg1,，pg2，…,，pgD）是種群的全局最優(yōu)位置矢量,。每次迭代過程中，粒子的速度和位置的更新公式為：

　　Vid（t+1）=wvid（t）+c1R1（pid-xid（t））+c2R2（pgd-xgd（t））（1）

　　xid（t+1）=xid（t）+vid（t）（2）

　　其中,，w為慣性權(quán)重,，c1、c2為加速因子,，R1,、R2為[0，1]之間的隨機數(shù)[1],。

　　通過解析式（1）和（2）可以發(fā)現(xiàn),，經(jīng)典的PSO算法的種群粒子在不斷的搜索過程中，常常跟蹤當前全局最優(yōu)位置及自己目前搜索到的歷史最優(yōu)位置,。因此,，粒子速度比較快地下降接近為0,，造成種群粒子陷入局部極小值而無法擺脫。這種“趨同性”局限了粒子的搜索空間,，若實現(xiàn)搜索空間的擴大,，必須要加大種群的粒子數(shù)，或降低種群粒子對全局最優(yōu)位置的追蹤,。加大粒子數(shù)會造成優(yōu)化問題的計算復雜度的增加,，降低種群粒子對全局最優(yōu)位置的追蹤又造成算法收斂性能較差的不足。

2 一種改進的多群協(xié)作粒子群優(yōu)化算法

　　2.1 MCPSO算法

　　牛奔[3]等人提出的基本MCPSO算法,，借鑒了生物系統(tǒng)中的共生現(xiàn)象,，反映了種群個體之間的相互關系。該算法將種群均分成具有主從模式的一個主群和多個從群,，利用主,、從群間的共生關系，兩者進行信息的交流與傳遞,，某種程度上克服了粒子陷入局部最優(yōu)的危險,。根據(jù)不同的共生關系，算法可分為合作（COL_MCPSO）和競爭（COM_MCPSO）兩種形式,，算法中每個從群都獨立并行地執(zhí)行基本PSO算法或其變體,，更新粒子的位置和速度。當所有從群更新完成,，再將局部最優(yōu)值傳給主群,。

　　（1）COL_MCPSO算法主群粒子位置,、速度更新公式為：

　　2.2 IMPSCO算法

　　面對高維,、多峰值的復雜優(yōu)化問題，為了獲得更好的全局最優(yōu)值,，基本MCPSO算法通過犧牲收斂速度來增加種群多樣性,，以達到降低種群陷入局部極小值的可能。但是同時保持種群多樣性和較快的收斂速度,，仍然是目前優(yōu)化算法面臨的一個挑戰(zhàn),，并且在搜索初期，多種群并行獨立搜索解空間,，造成部分粒子的重復搜索現(xiàn)象,，且種群搜索初期容易陷入局部最優(yōu)解。

　　2.3 改進算法

　　針對上述算法不足之處,，本文通過基本MCPSO算法中競爭結(jié)果,，即以COM_MCPSO算法為主要研究算法，提出了一種改進的多群協(xié)作粒子群優(yōu)化算法,。該算法利用一個主群和多個從群結(jié)構(gòu)協(xié)作進化,，其中從群粒子根據(jù)本粒子群迄今搜索到的最優(yōu)位置來更新種群中粒子速度，而主群是由所有從群的當前全局最優(yōu)位置來更新主群中的粒子速度,。多個從群改善了尋優(yōu)搜索過程中,，提高種群多樣性，擴大了解空間內(nèi)的搜索范圍,。同時,，主群粒子追逐當前的全局最優(yōu)位置來提高該算法的收斂速度，從而兼顧優(yōu)化過程的精度和效率,。這種算法各從群粒子數(shù)目并不要求相同,，每個子群的粒子位置和速度的更新策略也可以不同。當粒子數(shù)目相等的情況下,，IMCPSO與基本MCPSO算法的計算復雜度是相同的,。

　　該算法提出增加擾動因子的策略，即假設目前尋優(yōu)得到的全局最優(yōu)位置在連續(xù)的l次迭代都沒有更新,，則在搜索空間內(nèi)重新賦值粒子速度,。l為自然數(shù)，本文中稱作擾動因子,。其擾動策略的更新公式為：

　　if t-tl>l then reset v,；

　　其中tl表示為主群當前更新到全局最優(yōu)位置的迭代步數(shù)。

　　擾動策略的原理為：假如種群陷入局部極小值時,，重新隨機化粒子速度,，迫使種群粒子跳出局部極小值，進而進行下一迭代的新的搜索過程,。IMCPSO算法利用擾動因子的策略,，能夠進一步提高MCPSO算法的性能。

　　IMCPSO算法的步驟：（1）設置算法參數(shù)大小,，初始化主群和從群粒子的位置和速度,。（2）評估主群和從群中每個粒子的適應值，求解各從群的全局最優(yōu)值及整個種群的全局最優(yōu)位置,。（3）利用式（1）,、（2），更新全部從群粒子,，并評估從群的各粒子的適應值,。（4）將從群的全局最優(yōu)位置傳給主群，并根據(jù)式（5）,、（6）更新主群的各個粒子,，然后評估主群各粒子的適應值。（5）假如t-tl>l1主群全局最優(yōu)位置未更新則執(zhí)行步驟（6）,，否則執(zhí)行步驟（7）,。（6）在搜索空間內(nèi)重置主群粒子速度,。（7）若滿足終止條件（達到最大迭代步數(shù)）終止，返回主群的全局最優(yōu)值及適應值,；否則返回步驟（3）,。

3 實驗設計與結(jié)果分析

　　3.1 基準函數(shù)

　　為了保證實驗對比的準確性，IMCPSO和MCPSO算法參數(shù)設置為一個主群和4個從群,，每個子群粒子個數(shù)為5,，c1=c2=c3=1.494 45，wmin=0.4,，wmax=0.9,，其中vmax限制為搜索范圍的20%。擾動因子l=10,。

　　本文比較了IMCPSO與經(jīng)典PSO算法,、基本MCPSO算法，使用9個經(jīng)典的基準函數(shù)評估所提算法的性能,。測試基準函數(shù)與搜索范圍如下,。

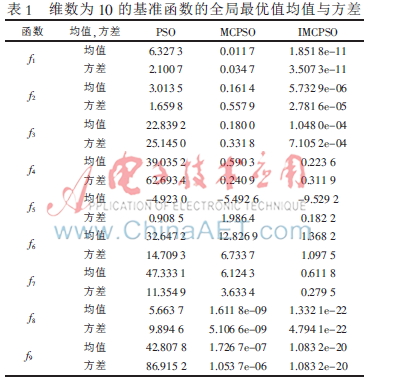
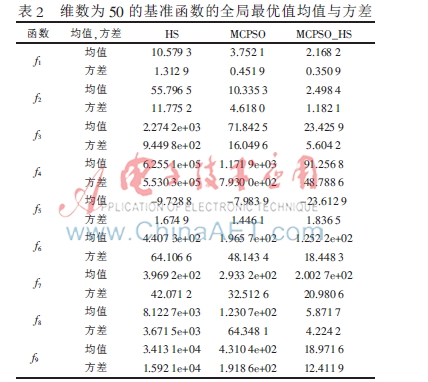
　　每個算法分別在維數(shù)為10、50的基準函數(shù)上測試,，迭代次數(shù)為1 000次,，運行100次。如表1,、表2中實驗結(jié)果為種群全局最優(yōu)值的均值和標準差,，IMCPSO和MCPSO-HS列代表函數(shù)相應的全局最佳適應值，所有結(jié)果的表達形式為“0.0000e+00”,。IMCPSO算法的最佳適應值平均值與標準差要好于PSO和MCPSO算法,，說明所提算法具有較好的穩(wěn)定性。

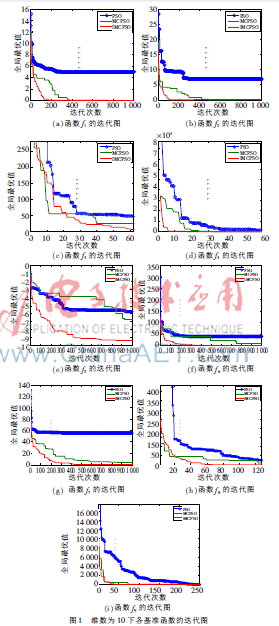
　　為表明算法的收斂速度,，在Windows7系統(tǒng),、Intel（R）4 3.20 GHz CPU、2 GB RAM,、軟件為MATLAB 2012a的環(huán)境下運行所提算法,，并得出在維數(shù)為10下各基準函數(shù)的迭代過程，如圖1所示,?？芍狪MPSCO算法的收斂速度和最優(yōu)值明顯優(yōu)于PSO和MCPSO算法。

　　本文中IMCPSO算法通過多個從群改善種群多樣性,，擴大了搜索范圍,，通過統(tǒng)一的初始化操作，避免了搜索空間的重復搜索。該算法引入擾動策略,，進一步避免了種群粒子陷入局部最優(yōu)點的危險,。實驗結(jié)果表明，與PSO和MCPSO算法相比,，IMCPSO算法更有效地使用了以往的解決方案,，以便獲取較好的全局最優(yōu)位置,。通過測試的9個基準函數(shù),，可以得出IMCPSO算法在解決高維、多峰值復雜優(yōu)化函數(shù)改善了PSO和MCPSO算法的尋優(yōu)性能和求解精度,，且具有較強的魯棒性,。

　　參考文獻

　　[1] KENNEDY J， EBERHART R C. Particle swarm optimization[C]. Proceedings of IEEE International Conference on Neural Networks,， piscataway,， 1995： 1942-1948.

　　[2] EBERHART R C， KENNEDY J. A new optimizer using particle swarm theory[C]. Proceedings of the Sixth International Symposium on Micro Machine and Human Science. 1995（1）： 39-43.

　　[3] Niu Ben,， Zhu Yunlong,， He Xiaoxian， et al. MCPSO： A multi-swarm cooperative particle swarm optimizer[J]. Applied Mathematics and Computation,， 2007,， 185（2）： 1050-1062.

　　[4] ZHAO S Z， SUGANTHAN P N,， PAN QUAN-KE,， et al. Dynamic multi-swarm particle swarm optimizer with harmony search[J]. Expert Systems with Applications， 2011,， 38（4）： 3735-3742.

　　[5] KONSTANTINOS E P. Parallel cooperative micro-particle swarm optimization： A master-slave model[J]. Applied Soft Computing,， 2012， 12（11）： 3552-3579.