《電子技術(shù)應(yīng)用》
您所在的位置：首頁(yè) > 通信與網(wǎng)絡(luò) > 設(shè)計(jì)應(yīng)用 > 中繼OFDMA系統(tǒng)用戶公平性的 資源分配算法的研究
中繼OFDMA系統(tǒng)用戶公平性的 資源分配算法的研究
2015年電子技術(shù)應(yīng)用第2期
黃靖然,，王 芳,，楊守義
鄭州大學(xué) 信息工程學(xué)院,，河南 鄭州450001
摘要： 在OFDMA解碼—轉(zhuǎn)發(fā)中繼系統(tǒng)中，為了公平地進(jìn)行資源分配,，提出了在兩個(gè)用戶模型下,，在保證每個(gè)用戶最小速率需求的前提下，先按照用戶預(yù)定速率比進(jìn)行子載波分配,，再根據(jù)實(shí)際速率比對(duì)用戶的子載波進(jìn)行調(diào)整的分配算法,，最后使整個(gè)系統(tǒng)的吞吐量達(dá)到最大。提出了三種方案,。方案一通過對(duì)Lagrange對(duì)偶函數(shù)問題的求解,，根據(jù)所得代價(jià)函數(shù)值的大小對(duì)用戶的子載波做重新調(diào)整。這樣不僅考慮到了公平性,，也減少了用戶的速率損失,。方案二、方案三分別從子載波端和用戶端出發(fā)考慮子載波的分配問題,，且從不同的分配角度分析了公平性問題,。研究結(jié)果表明，三種方案獲得的公平性均有所提高。
中圖分類號(hào)： TN929.5
文獻(xiàn)標(biāo)識(shí)碼： A
文章編號(hào)： 0258-7998(2015)02-0097-04
Study on the fairness and resource allocation for OFDMA relay networks
Huang Jingran,，Wang Fang,，Yang Shouyi
School of Information Engineering，Zhengzhou University, Zhengzhou 450001,，China
Abstract： In this paper,，in order to be fair to the allocation of resources, we propose a new resource allocation algorithm that allocates subcarriers according to the rate proportional of each user firstly, then adjusts the subcarriers according to the actual rate proportionally, and maximizes the system capacity at last in the decoding and forward OFDMA two relay and two users system. We put forward three schemes. Scheme one: By optimizing the Lagrangian dual function, we allocate subcarriers again according to the function, which can be viewed as the price for the power consumption. By doing so it can reduce the rate of loss of users when considering fairness. Scheme two and scheme three consider the subcarrier allocation from subcarrier and user holds respectively. They analyize the fairness problem from different aspects. Numerical results show that the proposed three schemes can improve the fairness of users.
Key words : OFDMA；relay systems,；fairness; resource allocation

　

0 引言

　　正交頻分多址（OFDMA)中繼通信系統(tǒng)覆蓋域大,、可擴(kuò)展性強(qiáng)，相比傳統(tǒng)的無線網(wǎng)絡(luò)可以有效提高系統(tǒng)容量,，是LTE網(wǎng)絡(luò)的關(guān)鍵技術(shù)之一[1]。OFDMA 中繼系統(tǒng)能獲得更高的峰值數(shù)據(jù)速率,、頻譜利用率,、更好的小區(qū)邊緣用戶等性能, 是廣大研究人員關(guān)注的焦點(diǎn)[2]。其通信系統(tǒng)中的資源分配問題也逐漸成為當(dāng)今的研究熱點(diǎn),。

　　根據(jù)中繼節(jié)點(diǎn)對(duì)接收信號(hào)處理方式的不同可以分為放大-轉(zhuǎn)發(fā)(Amplify and Forward,，AF)和解碼-轉(zhuǎn)發(fā)(Decode and Forward，DF)方式,。AF方式是中繼節(jié)點(diǎn)對(duì)接收到的信號(hào)進(jìn)行模擬處理,，將信號(hào)放大后轉(zhuǎn)發(fā)給目的節(jié)點(diǎn)，這樣就存在放大噪聲傳遞的缺點(diǎn),。而DF方式,，是中繼將接收到的信號(hào)進(jìn)行解調(diào)、解碼（如果編碼）和判決,，然后再將信號(hào)重新編碼后轉(zhuǎn)發(fā)給接收端,。

　　關(guān)于OFDMA資源分配問題的研究目前也備受關(guān)注。文獻(xiàn)[3]在DF中繼模型下,，研究了滿足QoS下的中繼選擇,、功率分配與子載波分配的聯(lián)合優(yōu)化問題。文獻(xiàn)[4]是在單中繼系統(tǒng)模型下,，討論了總功率約束下的用戶間的公平性,，并考慮了每個(gè)用戶均有各自的速率需求。文獻(xiàn)[5]是滿足每個(gè)用戶的子載波最小需求數(shù)目下獲得的公平性的提高,。文獻(xiàn)[6]是在限定的總功率,、誤碼率和速率比例下引入了均衡因子，對(duì)系統(tǒng)容量和用戶公平性之間的均衡進(jìn)行控制,。

　　目前,，現(xiàn)有的文獻(xiàn)中，在OFDMA中繼系統(tǒng)模型下考慮用戶公平性的情況，基本上是在給定的功率下,，根據(jù)用戶的預(yù)定速率比調(diào)整子載波,。未曾討論過提高公平性付出的代價(jià)導(dǎo)致了用戶的速率降低。文獻(xiàn)中也只是單純地從用戶角度考慮載波分配問題,，未曾考慮過怎樣調(diào)整子載波使其速率損失降低最少,，而后再去考慮功率優(yōu)化分配的問題。在本文中,，研究了子載波分配與功率分配聯(lián)合優(yōu)化下用戶公平性的問題,。且從不同角度考慮資源分配問題，并做了相互比較,。算法一是使得用戶間的速率比盡可能達(dá)到預(yù)定速率比的同時(shí),，也要保證其速率損失盡可能最小。算法二,、算法三則體現(xiàn)了從不同角度進(jìn)行載波分配的情況,。仿真結(jié)果表明，提出的三種算法中,，公平性都得到了提高,，但系統(tǒng)的平均吞吐量卻有所降低。且公平性達(dá)到越好,，付出的速率損失代價(jià)就越大,。

1 系統(tǒng)模型

　　本文為DF方式中繼模型下的OFDMA上行鏈路系統(tǒng)，其中包含兩個(gè)源節(jié)點(diǎn)S,，兩個(gè)中繼節(jié)點(diǎn)R和一個(gè)目的節(jié)點(diǎn)D,。這里要求每個(gè)用戶的信息均通過中繼轉(zhuǎn)發(fā)給目的，即不存在S到D的直接鏈路,。傳輸分為兩個(gè)時(shí)隙：第一時(shí)隙S向R發(fā)送信息,，R接收信息并進(jìn)行解碼；第二時(shí)隙R將編碼后的信息轉(zhuǎn)發(fā)給D,。

001.jpg

　　圖1中,，S-R、R-D,、S-D的子載波m的信道增益分別為1..png

2 優(yōu)化問題與分析

　　在DF中繼方式下,，總功率3IRE}@TBO48I0RZ[SEJ1}38.jpg~4([3D{@V1ADY(GS25(A9(N.png分別為源端和中繼端的功率。

　　要使速率最大,，則：

　　13.png

　　a為等效信道增益：

　　4.png

　　等效速率為：

　　5.png

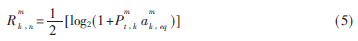
　　本文考慮每個(gè)用戶,、每個(gè)中繼均有各自的功率限制，且每個(gè)用戶均有最小速率要求,在這些約束條件下,，最大化系統(tǒng)容量,。目標(biāo)函數(shù)如下：

　　613.png

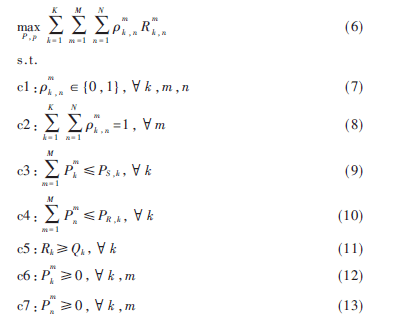
　　其中式(7),、(8)是指對(duì)于一個(gè)子載波最多分配給一個(gè)用戶和一個(gè)中繼。式(9),、(10)分別為源端和中繼端各自的功率約束,。式(11)為每個(gè)用戶的最小速率需求。

3 算法分析

　　3.1 算法一

　　算法一是通過對(duì)Lagrange對(duì)偶函數(shù)問題求解分析,，根據(jù)所得代價(jià)函數(shù)H,，再次調(diào)整子載波時(shí)將對(duì)于該用戶H值最小的子載波移給對(duì)方。這樣不僅考慮到用戶間的公平性,，也保證了其速率損失盡可能最小,。

　　式(6)的目標(biāo)函數(shù)為凸函數(shù)，利用Lagrange對(duì)偶法[8]求解式(6)～(13),，問題轉(zhuǎn)化為：

　　1416.jpg

　　17.jpg

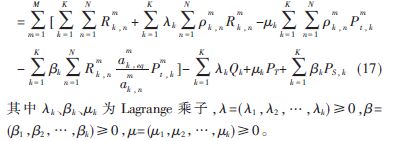
　　優(yōu)化問題轉(zhuǎn)化為：

　　18.png

　　根據(jù)文獻(xiàn)[4],，對(duì)于每一個(gè)子載波m，可以分解為M個(gè)次優(yōu)問題,，則：

　　1921.png

　　根據(jù)Karush-Kuhn-Tucker(KKT)條件[8],，最后可以得到子載波m的最優(yōu)功率：

　　22.png

　　帶入可得：

　　2324.png

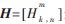　　XTF_TEFR{(`8J91M(D59E4M.jpgXTF_TEFR{(`8J91M(D59E4M.jpg是K×N的矩陣，定義為代價(jià)函數(shù),，是子載波m分別對(duì)應(yīng)用戶1、用戶2,、中繼1,、中繼2的能量功耗代價(jià)函數(shù)值，值越大,，子載波m即分配給相應(yīng)的用戶和中繼,。

　　可以表示為：

　　25.png

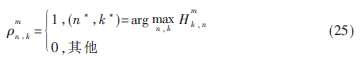
　　方案1分配子載波的流程如下：

　　(1)按照式(25)將所有的子載波分配給對(duì)應(yīng)的用戶和中繼。

　　(2)將用戶1,、用戶2所分配到的子載波對(duì)應(yīng)的代價(jià)函數(shù)值H存儲(chǔ)在S1,、S2中，按照函數(shù)值從大到小的順序排列,。

　　(3)先分別計(jì)算出用戶1,、用戶2已分得的子載波個(gè)數(shù)N1、N2,。再根據(jù)預(yù)定速率比與總共的子載波數(shù)目,，算出兩個(gè)用戶預(yù)定子載波個(gè)數(shù)N1?鄢、N2?鄢,。若此時(shí)N1>N1?鄢,，則將用戶1中S1的后(N1-N1?鄢)個(gè)子載波分配給用戶2，這樣保證了用戶1移走子載波后,，對(duì)其速率影響不會(huì)太大,；反之同理,。這樣，按照子載波個(gè)數(shù)比等于預(yù)定速率比,，初步完成了兩個(gè)用戶子載波的分配,。

　　(4)最后再次計(jì)算用戶1和用戶2的實(shí)際速率比Q，若Q>Q?鄢（或Q<Q?鄢）,，則再次調(diào)整子載波,，直到Q接近于預(yù)定速率比。

　　3.2 算法二

　　算法二的子載波分配方案是從子載波端出發(fā),，按照3.1.1中介紹的,，根據(jù)矩陣H中的取值，找出每個(gè)子載波對(duì)應(yīng)的最優(yōu)用戶與最優(yōu)中繼,。分配過程中若其中某一用戶分配完所需的子載波,，即停止對(duì)他的分配，將剩余的子載波全部分配給另一用戶,。最后根據(jù)實(shí)際的速率比,，再次對(duì)兩個(gè)用戶的子載波做相應(yīng)調(diào)整。此算法子載波分配的速度較快,。

　　由于本文是速率最大化,，即使兩個(gè)用戶按照預(yù)定比例速率分配子載波，但在利用注水算法分配功率時(shí)仍會(huì)按照用戶的最大功率限制分配完所有功率,，即：即使一個(gè)用戶分配了少量的子載波,，但每個(gè)子載波上的功率會(huì)很大（因?yàn)榇藭r(shí)相當(dāng)于水平面變高，衡量的標(biāo)準(zhǔn)不一）,。這樣,，比較兩個(gè)用戶的實(shí)際速率時(shí)，無法體現(xiàn)出公平性,。

　　本文在分配功率時(shí)進(jìn)行了改進(jìn),。第一步，為兩個(gè)用戶分配預(yù)定的子載波,，再進(jìn)行功率分配,。第二步，根據(jù)兩個(gè)用戶的實(shí)際速率,，再次調(diào)整子載波,。這里假設(shè)用戶1將自己的一個(gè)子載波移給用戶2。調(diào)整完子載波后,，再進(jìn)行功率的重新分配,。這里重新分配功率時(shí)，用戶1仍按照原先數(shù)量的子載波分配功率,，而再次獲得子載波的用戶2卻按照現(xiàn)有的子載波分配功率,。但分配完功率后,，在計(jì)算實(shí)際速率時(shí)，用戶1卻要去除分走的子載波及其上的功率,，只計(jì)算調(diào)整后的子載波上的速率,。用戶2則計(jì)算現(xiàn)有子載波速率即可。

　　3.3 算法三

　　算法三的子載波分配方法是從用戶端出發(fā),，定義兩用戶最簡(jiǎn)速率比Q1?鄢：Q2?鄢=Q?鄢,，那么每次給用戶1、用戶2分配子載波時(shí)就按照子載波個(gè)數(shù)比等于速率比依次分配（n1:n2=Q1:Q2）,，直到分配完所有的子載波,。

　　算法三的功率分配方案與算法二相同。

4 仿真分析

　　本節(jié)給出了上述幾種算法的仿真結(jié)果與分析,。信道衰落為獨(dú)立同分布且均值為1的瑞利衰落,。子載波數(shù)目為50。用戶端與中繼端允許的最大功率為1,。

002.jpg

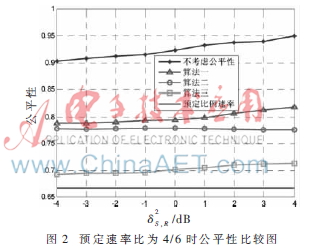
　　圖2給出了用戶1與用戶2的速率比例曲線,，兩個(gè)用戶的最小速率分別為0.4 bps/Hz、0.6 bps/Hz,。仿真圖中,，最下邊的曲線為預(yù)定比例速率曲線?？梢钥闯鰶]有考慮公平性時(shí),，公平曲線偏離預(yù)定曲線最遠(yuǎn)。其次,離預(yù)定公平曲線最近的是算法一得到的曲線,，依次往上的兩條曲線分別是算法二和算法三的仿真曲線?？梢钥闯?，算法三得到的公平性效果最好，算法二次之,，算法一有相應(yīng)提高,。

003.jpg

　　圖3中是對(duì)應(yīng)的用戶平均吞吐量曲線。其中算法一,、算法二,、算法三是已調(diào)整速率后的平均吞吐量曲線。當(dāng)然,，從圖中可以看出,，吞吐量達(dá)到最大的是不考慮公平性的算法，因?yàn)樗皇歉鶕?jù)信道增益的大小分配子載波,。在本文提出的三種算法中,，由于考慮了公平性需重新調(diào)整子載波,，當(dāng)然分配的功率也有所變化，這樣最后得到的吞吐量比不考慮公平性的要降低一些,。其中,，算法一雖然公平性提高的不多，但吞吐量高于其余兩種算法,。算法二與算法三的吞吐量依次減少,。可以看出公平性的提高是以速率損失為代價(jià)的,。

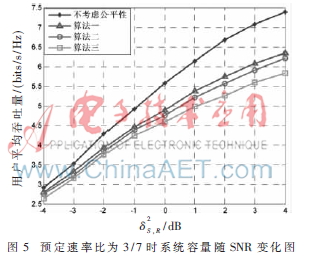
　　圖4,、圖5分別是兩個(gè)用戶最小速率為0.3 bps/Hz、0.7 bps/Hz時(shí)對(duì)應(yīng)的公平性和速率圖,。從圖4中可以看出,，此時(shí)用戶1、用戶2預(yù)定速率比為3/7,，比圖2中低（預(yù)定速率比為4/6）,。其對(duì)應(yīng)的三種算法得到的公平性曲線當(dāng)然也比圖2中低。其中算法三得到的公平性更接近于預(yù)定比例速率（3/7）,。但它們都無法達(dá)到預(yù)定比例速率,。從圖5中可以看到，這時(shí)付出的速率損失比圖3中的更多一些,，并且算法三得到的系統(tǒng)容量降低更多,。

5 結(jié)束語(yǔ)

　　本文針對(duì)OFDMA多中繼多用戶系統(tǒng)下，研究了用戶公平性的問題,，并提出了三種算法,。最后進(jìn)行了仿真分析與比較。仿真結(jié)果表明,，用戶公平性的提高是以降低了系統(tǒng)吞吐量為代價(jià)的,。提出的三種算法在某種程度上都提高了用戶的公平性，但公平性達(dá)到越好,，速率損失也會(huì)相應(yīng)的有所增加,。因此，怎樣更好地權(quán)衡公平性與速率損失是下一階段研究的重要問題,。

參考文獻(xiàn)

　　[1] ZHOU N,，ZHU X，HUANG Y.Adaptive resource allocation formulti-destination relay systems based on OFDM modulation[C].Proceedings of the 2009 IEEE International Conference on Communications.Dresden：IEEE,，2009：1-5.

　　[2] GENC V,，MURPHY S，YU Y.IEEE 802.16j relay-based wireless access networks: a novel view[J].IEEE Wireless  Communication,，2008,，15：56-65.

　　[3] ALAM M S,，MARK J W.Shen X.Relay selection and resource allocation for multi-user cooperative OFDMA networks[J].IEEE Wireless Communication，2013,，12(5)：2193-2205.

　　[4] 萬(wàn)慶濤,，馬冠一.中繼OFDMA系統(tǒng)容量公平資源分配算法研究[J].計(jì)算機(jī)工程與應(yīng)用，2011,，47（8）：21-24.

　　[5] MUNASINGHE G,，JAYALATH D.Subcarrier pairing and relay assignment with improved user fairness in a multi-user cooperative OFDM system[J].IEEE，2012.

　　[6] 鄭懷棟,，潘甦.OFDMA系統(tǒng)資源分配算法研究[D].南京：南京郵電大學(xué),，2011.

　　[7] DANG M，TAO M,，MU H.Subcarrier-pair based resourceallocation for cooperative multi-relay OFDM systems[J].IEEE Trans.Wireless Communication,，2010，9(5)：1640-1649.

　　[8] BOYD S,，VANDENBERGHE L.Convex optimization[M].Cambridge：Cambridge University Press,，2004.


此內(nèi)容為AET網(wǎng)站原創(chuàng)，未經(jīng)授權(quán)禁止轉(zhuǎn)載,。