摘  要： 作為一種新興的群智能優(yōu)化方法,，螢火蟲算法具有簡單易懂,、參數(shù)少和易實現(xiàn)等優(yōu)點,，已經(jīng)在諸多領(lǐng)域取得了較好的應(yīng)用。為了使該算法能夠更有效地解決不同的優(yōu)化問題，需要對標準螢火蟲算法進行改進或混合其他算法,。介紹了螢火蟲算法的原理及其應(yīng)用領(lǐng)域,，重點分析了算法的改進策略,，并提出了算法進一步研究的方向,。
　　關(guān)鍵詞： 群智能；螢火蟲算法,；混合算法,；優(yōu)化
0 引言
　　群智能是一種通過簡單個體的行為，以某種形式聚集協(xié)同,，使群體在沒有集中控制的情況下所表現(xiàn)出的智能行為[1],。群智能優(yōu)化算法是一種對自然界中生物的群體行為的模擬，并用數(shù)學(xué)形式表達出來的方法,。典型的群智能優(yōu)化算法有兩個,，即蟻群優(yōu)化算法（Ant Colony Optimization，ACO）和粒子群優(yōu)化算法（Particle Swarm Optimization，PSO）,。
　　劍橋?qū)W者Yang Xinshe根據(jù)螢火蟲個體的發(fā)光特性和相互吸引的行為,，于2008年提出了螢火蟲算法（Firefly Algorithm，F(xiàn)A）[2],。FA是繼PSO和ACO之后,，又一新穎的群智能啟發(fā)式優(yōu)化算法，具有概念簡單,、需要調(diào)整的參數(shù)少,、易于應(yīng)用和實現(xiàn)等優(yōu)點,。螢火蟲算法是一種高效的優(yōu)化算法,，已成為眾多學(xué)者研究的熱點，在諸多領(lǐng)域得到了較好的應(yīng)用,。但標準螢火蟲算法無法有效解決不同的優(yōu)化問題,，因此需要對其進行改進研究。
1 標準螢火蟲算法
　　螢火蟲算法是基于以下三個理想化的特征提出的：（1）螢火蟲不分性別,，即螢火蟲之間的相互吸引只考慮個體發(fā)光的亮度,；（2）吸引力與發(fā)光亮度成正比，與個體之間的距離成反比,；（3）螢火蟲的亮度由待優(yōu)化的目標函數(shù)值決定,，即Ii=f（xi）。
　　FA的關(guān)鍵思想是亮度小的螢火蟲被亮度大的螢火蟲吸引而向其移動,，并更新自身的位置,。螢火蟲的發(fā)光亮度取決于自身所處位置的目標值，亮度越高所表示的目標值越好,，吸引其他螢火蟲的能力也越強,。若相鄰的個體亮度相同，螢火蟲則隨機移動,。為了方便算法模型的建立,，給出如下定義[2]：
　　定義1 亮度

       其中，I0為初始光強度,，即在光源（r=0）處的光強度,。
　　定義2 吸引力

　　其中，m值通常取2,；為最大吸引力,，即光源（r=0）處的吸引力，對于大多數(shù)的應(yīng)用問題,，可取為1,；參數(shù)是空氣對光的吸收率，影響吸引力的變化,，值的選取對算法性能有很大的影響,，理論上∈[0,，∞），但在實際應(yīng)用中,，常取∈[0.1,，10]。rij為螢火蟲i到j(luò)的笛卡爾距離,，表達式為：

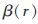　　參考文獻[2]指出,，在實際應(yīng)用中，吸引力函數(shù)可以是任何一種單調(diào)遞減函數(shù),，例如：

　　定義3 位置更新公式
　　螢火蟲j被螢火蟲i吸引而向i移動更新自己的位置：

　　其中,，t為算法迭代次數(shù)；xi,、xj為螢火蟲和j所處的位置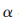,；為隨機步長，一般取值范圍為[0,，1],；εj通常是由高斯分布、均勻分布或其他分布生成的隨機數(shù)向量,。標準螢火蟲算法需要執(zhí)行算法初始化,、螢火蟲位置更新、螢火蟲亮度更新,、解的評估等操作,，算法流程如圖1所示。

2 螢火蟲算法的研究與改進
　　FA的提出吸引了很多學(xué)者對其進行研究,。Yang Xinshe用FA優(yōu)化帶有奇點的測試函數(shù),，結(jié)果顯示FA能有效解決這類優(yōu)化問題[3]，并將FA成功應(yīng)用到壓力管道設(shè)計優(yōu)化問題中,。但是,，標準FA中的參數(shù)都是事先設(shè)定的，會導(dǎo)致算法收斂早熟,，或因參數(shù)設(shè)置不當而導(dǎo)致算法無法收斂,。為了使算法具有較好的優(yōu)化性能，需要對標準FA進行改進,。
　　Yang Xinshe首先把Levy Flight引入到式（5）的隨機部分,，構(gòu)建了具有Levy Flight的螢火蟲算法（Levy-Flight Firefly Algorithm，LFA）[4],。分別用LFA和遺傳算法（Genetic Algorithm,，GA）優(yōu)化標準測試函數(shù)，結(jié)果顯示LFA能更高效、準確地搜索全局最優(yōu)值,。FATEEN S E K等人提出智能螢火蟲算法（Intelligent Firefly Algorithm,，IFA）[5]，該算法將螢火蟲按亮度排列后,，確定適應(yīng)度較好的個體的比例及頂部螢火蟲數(shù)量,，每次迭代螢火蟲都向頂部螢火蟲移動并更新位置。實驗證明IFA能高效解決全局優(yōu)化問題,，避免算法收斂早熟,。此外，學(xué)者們還提出了各自不同的改進方法,。
　　2.1 基于自適應(yīng)策略的FA
　　FARAHANI S M等人[6]采用自適應(yīng)步長改進了FA的隨機部分,，給隨機步長定義一個依賴于迭代次數(shù)的系數(shù)，迭代初期采用較大的步長,，搜索較大的區(qū)域,，迭代后期減小步長，使算法快速收斂于全局最優(yōu)點,。同時還提出了螢火蟲的定向移動，即在沒有局部更亮的個體時,，螢火蟲向全局最優(yōu)點移動,。這種改進提高了算法精度，也減少了螢火蟲的無效運動,。實驗結(jié)果表明,，改進算法的優(yōu)化效果優(yōu)于標準FA。
　　FA對寬搜索區(qū)域和高維度優(yōu)化問題存在吸引力很弱難以影響位置更新的現(xiàn)象,。據(jù)此,，董靜提出根據(jù)rij調(diào)節(jié)隨機參數(shù)的方法，用2rij（rand-1/2）取代式（5）中的隨機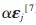部分,。隨機步長隨rij變化,，當rij較大時，吸引力則較小,，螢火蟲本身在[-rij,，rij]范圍內(nèi)自由移動，加強了算法的探索能力,；當rij較小時,，算法進行局部尋優(yōu)，此時吸引力對位置更新占主導(dǎo)作用,。這種改進提高了算法的尋優(yōu)精度和收斂速度,。Yan Xiaohui等人則提出壓縮距離的方法[8]。式（2）中，令m∈（0,，1）,，此時若rij值很大，則rijm的值就會相應(yīng)變小,，保證在合理范圍之內(nèi),。其中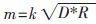，k是常數(shù),，通常取O（1）,，D代表維度，R代表搜索范圍,，對于不同的優(yōu)化問題,，m值各不相同。改進后的FA在解決高維優(yōu)化問題時,，效果明顯優(yōu)于標準FA,、PSO和差分進化算法（Differential Evolution，DE）,。
　　Yu Shuhao等人提出了根據(jù)每只螢火蟲的歷史信息和當前位置信息來確定隨機步長的策略[9],，使靠近最優(yōu)解的個體具有較小的步長，而遠離最優(yōu)解的個體具有大一些的步長,，從而更新螢火蟲的位置,。因此，每只螢火蟲下一次迭代的步長都是自適應(yīng)的,，且由當前最優(yōu)值與群體最優(yōu)值之間的差異決定,。這種改進方法能避免算法收斂早熟，提高了螢火蟲算法的準確度,。
　　2.2 基于參數(shù)調(diào)節(jié)的FA
　　dos Santos Coelho L在標準FA中引入混沌思想,，用混沌序列調(diào)節(jié)參數(shù)，避免算法陷入局部最優(yōu),，并用該算法優(yōu)化可靠性冗余分配問題,，取得了更好的結(jié)果。FARAHANI S M等人在標準FA中引入自動學(xué)習(xí)機調(diào)節(jié)參數(shù)],，使得算法能夠根據(jù)環(huán)境隨時調(diào)整參數(shù)值,。實驗結(jié)果表明，改進后的FA在優(yōu)化性能上有很大提升,?；趨?shù)調(diào)節(jié)的FA在解決動態(tài)優(yōu)化問題方面取得了比PSO更好的結(jié)果。
　　2.3 混合螢火蟲算法
　　FARAHANI S M等人將GA混合到FA中來提高螢火蟲算法的全局搜索能力[11],?；旌纤惴▽⒎N群分為兩個子群,，分別執(zhí)行FA和GA操作，在每次迭代的最后,，兩個子群相互交換并進入下一次迭代,，同時采用高斯隨機步長使螢火蟲在搜索空間移動，克服了標準FA中隨機步長固定不變的缺點,。GA的引入使FA的勘探和開采能力得到平衡,，該改進算法具有優(yōu)于標準FA和PSO的優(yōu)化能力。
　　ABDULLAH A等人將DE算法融入標準FA中[12],。該混合算法將螢火蟲個體按適應(yīng)度值分為兩個子群,，第一個子群中包含適應(yīng)度較好的個體，執(zhí)行標準FA操作,；第二個子群中則包含適應(yīng)度不好的個體,，執(zhí)行DE算法的交叉、變異,、選擇操作,，最后從兩個子群中選取最優(yōu)解。該混合算法增加了螢火蟲之間的信息共享,，避免算法陷入局部最優(yōu),，提高了算法搜索效率。
　　Guo Lihong等人融合了標準FA與和聲搜索（Harmony Search,，HS）算法[13],，將HS的勘探能力與標準FA的開采能力相結(jié)合，HS的引入可以看作是變異操作,，保證了種群的多樣性，使得算法具有更好的尋優(yōu)性能,。同時,，還采用了頂部螢火蟲方案，降低了算法復(fù)雜度,。經(jīng)實驗驗證,，混合HS的螢火蟲算法比其他優(yōu)化算法能更好地利用有用信息來發(fā)現(xiàn)最優(yōu)解。
　　2.4 其他形式的FA
　　SAYADI M等人提出用于解決離散優(yōu)化問題的離散螢火蟲算法（Discrete Firefly Algorithm,，DFA）[14],，并用其成功解決了置換流水車間調(diào)度中最小化完工時間問題，其處理結(jié)果比ACO得到的結(jié)果更優(yōu),，實驗結(jié)果顯示DFA能很好地優(yōu)化不同規(guī)模的調(diào)度問題,。
　　FARAHANI S M針對動態(tài)優(yōu)化問題提出了一種基于多群體的螢火蟲算法[15]。該算法將螢火蟲種群分為一系列相互影響的子群體,，由排斥因子和抗收斂因子分別控制進行局部尋優(yōu)和全局尋優(yōu),，這樣可以保證每個子群的群體多樣性,，有效避免算法陷入局部最優(yōu)。用多群螢火蟲算法處理動態(tài)優(yōu)化問題,，其能力優(yōu)于PSO,。
　　Yang Xinshe提出了多目標螢火蟲算法[16]（Multiobjective Firefly Algorithm，MOFA）,，該算法根據(jù)Pareto支配關(guān)系確定螢火蟲的亮度大小,，在迭代過程中求得Pareto最優(yōu)解。用MOFA處理焊接梁工程優(yōu)化問題,，優(yōu)化結(jié)果表明,，MOFA是一種有效的優(yōu)化器。董靜也提到了MOFA,，用外部檔案保存Pareto解,，并用自適應(yīng)網(wǎng)格法維護外部檔案[7]。此方法為多目標螢火蟲優(yōu)化提供了方向,。
3 螢火蟲算法的應(yīng)用
　　螢火蟲算法主要應(yīng)用于優(yōu)化,、工程應(yīng)用及分類問題。優(yōu)化問題又分連續(xù)優(yōu)化,、組合優(yōu)化,、約束優(yōu)化、多目標優(yōu)化及動態(tài)或含噪聲優(yōu)化,。MAUDER T等人用FA解決連鑄工藝優(yōu)化問題[17],，在滿足約束條件的情況下，得到了滿意的結(jié)果,；FISTER Jr I等人用混合局部搜索的FA解決圖三著色問題,，并取得較好的結(jié)果[18]，該結(jié)果顯示了FA在解決其他組合優(yōu)化問題方面的潛力,。SENTHILNATH J等人用螢火蟲算法解決聚類問題[19],，并得出FA是處理聚類的有效方法。作為一種優(yōu)化工具,，F(xiàn)A及其改進算法還成功地應(yīng)用于圖像處理,、路徑規(guī)劃、天線設(shè)計等領(lǐng)域,，均取得了較好的結(jié)果,。隨著螢火蟲算法的不斷完善，其應(yīng)用領(lǐng)域也將會不斷擴大,。
4 結(jié)論
　　FA是一種高效的啟發(fā)式優(yōu)化算法,，但仍有許多方面需要進一步研究。參數(shù)的設(shè)置會影響FA的性能,，很多文獻都提出了有效的改進方法,，對參數(shù)進行選擇和控制,，提高了算法的優(yōu)化能力。尋找高效的參數(shù)控制方法,，是FA研究的一個重要方向,。混合螢火蟲算法能在一定程度上克服FA自身的缺點,，大大提高算法的性能,。目前FA已與GA、DE,、HS等算法融合,，尋找能夠有效結(jié)合的混合算法也是研究熱點之一。在應(yīng)用方面,，F(xiàn)A及其改進算法已廣泛應(yīng)用到諸多領(lǐng)域,，但在分類與識別問題方面的應(yīng)用偏少。將FA與機器學(xué)習(xí)結(jié)合應(yīng)用也是很有意義的,。此外,，如何用FA更好地解決動態(tài)優(yōu)化問題也是值得研究的。最后,，F(xiàn)A的數(shù)學(xué)理論尚不完善,，算法的復(fù)雜度和收斂性分析仍然具有研究性。
　　參考文獻
　　[1] CHRISTIAN B,， DANIEL M（Eds）.群智能[M].龍飛,，譯，北京：國防工業(yè)出版社,，2011.
　　[2] Yang Xinshe. Nature-inspired metaheuristic algorithms[M]. Luniver press,， 2010.
　　[3] Yang Xinshe. Firefly algorithm， stochastic test functions and design optimisation[J]. International Journal of Bio-Inspired Computation,， 2010,，2（2）：78-84.
　　[4] Yang Xinshe. Firefly algorithm， Levy flights and global optimization[M]. Research and Development in Intelligent Systems XXVI,， London： Springer， 2010.
　　[5] FATEEN S E K,， BONILLA-PETRICIOLET A. Intelligent firefly algorithm for global optimization[M]. Cuckoo Search and Firefly Algorithm,， Springer International Publishing， 2014.
　　[6] FARAHANI S M,， ABSHOURI A A,， NASIRI B， et al. An improved firefly algorithm with directed movement[C]. Proceedings of 4th IEEE International Conference on Computer Science and Information Technology,， Chengdu,， 2011： 248-251.
　　[7] 董靜.螢火蟲算法研究及其在水下潛器路徑規(guī)劃中的應(yīng)用[D].哈爾濱：哈爾濱工程大學(xué),，2013.
　　[8] Yan Xiaohui， Zhu Yunlong,， Wu Junwei,， et al. An improved firefly algorithm with adaptive strategies[J]. Advanced Science Letters， 2012,， 16（1）： 249-254.
　　[9] Yu Shuhao,， Yang Shanlin， Su Shoubao. Self-adaptive step firefly algorithm[J]. Journal of Applied Mathematics,， 2013.
　　[10] dos Santos Coelho L,， de Andrade Bernert D L， Mariani V C. A chaotic firefly algorithm applied to reliability-redundancy optimization[C]. 2011 IEEE Congress on Evolutionary Computation（CEC）,， IEEE,， 2011： 517-521.
　　[11] FARAHANI S M， ABSHOURI A A,， NASIRI B,， et al. Some hybrid models to improve firefly algorithm performance[J]. International Journal of Artificial Intelligence， 2012,， 8（S12）： 97-117.
　　[12] ABDULLAH A,， DERIS S， MOHAMAD M S,， et al. A new hybrid firefly algorithm for complex and nonlinear problem[M]. Distributed Computing and Artificial Intelligence,， Berlin Heidelberg Springer： 2012.
　　[13] Guo Lihong， Wang Gaige,， Wang Heqi,， et al. An effective hybrid firefly algorithm with harmony search for global numerical optimization[J]. The Scientific World Journal，2013,， Article ID 125625,，9.
　　[14] SAYADI M， RAMEZANIAN R,， GHAFFARI-NASAB N. A discrete firefly meta-heuristic with local search for makespan minimization in permutation flow shop scheduling problems[J]. International Journal of Industrial Engineering Computations,， 2010，1（1）：1-10.
　　[15] FARAHANI S M,， NASIRI B,， MEYBODI M R. A multiswarm based firefly algorithm in dynamic environments[C].Third International Conference on Signal Processing Systems（ICSPS2011）， 2011,，3：68-72.
　　[16] Yang Xinshe. Multiobjective firefly algorithm for continuous optimization[J]. Engineering with Computers,， 2013，29（2）： 175-184.
　　[17] MAUDER T,， SANDERA C,， STETINA J,， et al. Optimization of the quality of continuously cast steel slabs using the firefly algorithm[J]. Materials and technology， 2011,，45（4）：347-350
　　[18] FISTER Jr I,， Yang Xinshe， FISTER I,， et al. Memetic firefly algorithm for combinatorial optimization[J]. arXiv preprint arXiv：1204.5165,， 2012.
　　[19] SENTHILNATH J， OMKAR S N,， MANI V. Clustering using firefly algorithm： Performance study[J]. Swarm and Evolutionary Computation,， 2011，1（3）：164-171.