0 引言

    現(xiàn)代數(shù)控系統(tǒng),、工業(yè)機(jī)器人正向著高速和高精度的方向發(fā)展,，而加減速控制算法在實(shí)現(xiàn)其運(yùn)動的高速、高精度上起著至關(guān)重要的作用,。哈爾濱工程大學(xué)鄭金興等^[1]提出了基于梯形速度控制的變插補(bǔ)周期實(shí)時(shí)插補(bǔ)算法,，該算法可有效地控制加工精度，充分發(fā)揮了各軸聯(lián)動的加減速能力,，但在運(yùn)動的高速和實(shí)時(shí)性上不是很理想,；朱明等^[2]提出了一種實(shí)用的S曲線加減速控制算法，該算法加速度連續(xù)變化,，速度變化平穩(wěn),，減小了加工過程中速度突變造成的沖擊,但算法稍復(fù)雜，計(jì)算量大,。目前,，應(yīng)用于數(shù)控系統(tǒng)和工業(yè)機(jī)器人中的加減速運(yùn)動控制算法有很多,。如梯形曲線加減速、S形曲線加減速,、多項(xiàng)式加減速,、三角函數(shù)加減速^[3-4]等控制算法。這些加減速算法都可以通過軟件編程的方式實(shí)現(xiàn),，但由于計(jì)算量較大使得很難通過硬件編程的方式實(shí)現(xiàn),。為了減小計(jì)算量，實(shí)現(xiàn)加減速控制算法的高速與高精度,，Chen和LEE^[5]提出了基于FIR濾波器的加減速速度規(guī)劃算法,。該算法采用濾波技術(shù)對加減速度進(jìn)行光滑處理，實(shí)現(xiàn)了加減速的連續(xù)變化,，減少了加工中由于加減速突變而產(chǎn)生的振動,，進(jìn)而實(shí)現(xiàn)高精度加工，同時(shí)又能達(dá)到良好的加減速性能,，實(shí)現(xiàn)高速的加工,；但其算法稍復(fù)雜，實(shí)現(xiàn)上有一定的難度,。KIM D^[6]提出了一種基于卷積的加減速運(yùn)動規(guī)劃算法,。該算法通過對速度進(jìn)行卷積，使得在計(jì)算過程中只包含加法與除法運(yùn)算,，簡化了復(fù)雜的計(jì)算過程,，提高了加減速控制算法的運(yùn)算速度。

    本文在以上研究基礎(chǔ)上,，引入數(shù)字卷積,，采用FPGA硬件編程的方式實(shí)現(xiàn)數(shù)字卷積加減速控制算法，提高了運(yùn)算速度與精度,。該算法采用定點(diǎn)數(shù)進(jìn)行計(jì)算,，節(jié)約了FPGA的邏輯門的數(shù)量并且減小了計(jì)算誤差。

1 數(shù)字卷積加減速算法

    基于數(shù)字卷積加減速算法[7]卷積算子表達(dá)式為：

    由于式(2)是迭代表達(dá)式,，并且只包含加法和除法運(yùn)算,，因此采用FPGA硬件去實(shí)現(xiàn)將極大地降低計(jì)算量,。

    對于固定速度V_max輸入經(jīng)過一次數(shù)字卷積后得到如圖1所示的梯形加減速曲線,。其中，總的運(yùn)行時(shí)間nT_s等于曲線的長度除以固定速度V_max,。經(jīng)過數(shù)字卷積后速度的位移距離必須保持一致,，因此，H₁的值取為1/n₁T_s,。如果想要得到光滑,、高柔性的S形加減速速度曲線,，可以對固定速度輸入進(jìn)行兩次數(shù)字卷積，即對得到的梯形速度曲線再進(jìn)行一次數(shù)字卷積如圖2所示,。另外,，為了確保在經(jīng)過兩次數(shù)字卷積后能夠達(dá)到最大速度V_max，n₂T_s的時(shí)間必須小于n₁T_s,，否則在經(jīng)過數(shù)字卷積后得到的最大速度將小于固定的速度值V_max,。

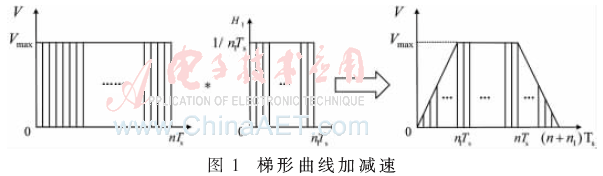
2 數(shù)字卷積加減速算法的硬件實(shí)現(xiàn)

2.1 梯形加減速算法的實(shí)現(xiàn)

    對于單軸點(diǎn)對點(diǎn)的梯形加減速運(yùn)動，S為總的運(yùn)動距離,，V_max為最大速度,，N₁為梯形加減速數(shù)字卷積序列長度?？偟倪\(yùn)行時(shí)間為S除以V_max,；在FPGA硬件設(shè)計(jì)時(shí)采用定點(diǎn)數(shù)進(jìn)行計(jì)算，在運(yùn)算過程中涉及到除法運(yùn)算,。因此,，為了減小誤差要考慮余數(shù)的問題。文中的運(yùn)動距離S,、速度V_max及余數(shù)之間的關(guān)系表達(dá)式如式(3)：

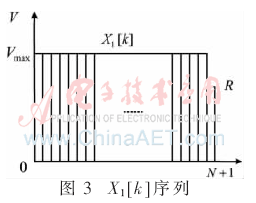
    其中,，N表示速度為V_max時(shí)的速度序列脈沖數(shù)，R為余數(shù),。另外,，輸入速度序列為X₁[k]，如圖3所示,。

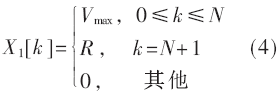
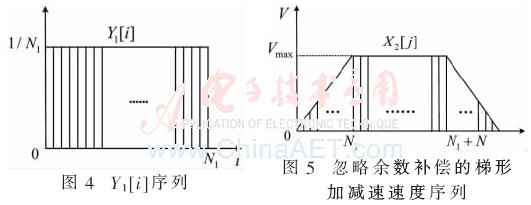
    卷積算子序列Y₁[i]如圖4所示,，數(shù)字卷積序列長度為N₁，其中N₁<N/2,。通過對X₁[k]與Y₁[i]進(jìn)行一次數(shù)字卷積得到梯形加減速運(yùn)動控制速度序列如圖5所示,，其表達(dá)式為式(5)：

    如果忽略余數(shù)R，在運(yùn)動過程中將出現(xiàn)速度誤差,，進(jìn)而導(dǎo)致位置誤差,。為了解決這個(gè)問題，本文采用速度補(bǔ)償?shù)姆绞?，在速度序列的末尾添加補(bǔ)償速度序列來消除余數(shù)誤差,，得到的速度輸出序列如圖6所示。

2.2 S形曲線加減速算法的實(shí)現(xiàn)

    如果對X₁[k]進(jìn)行兩次數(shù)字卷積將得到S形加減速曲線,；對于S曲線加減速,，第二次數(shù)字卷積的序列長度為N₂。為了保證在經(jīng)過兩次數(shù)字卷積后,，能夠達(dá)到最大速度V_max,，N₂的取值必須小于N₁,，卷積算子序列Y₂[n]如圖7所示。通過X₂[j]與Y₂[n]進(jìn)行數(shù)字卷積可得到S形加減速曲線速度序列X₄[q],，如圖8所示,。

    與梯形加減速類似，如果忽略余數(shù)R將導(dǎo)致速度誤差和位置誤差,。為了解決這個(gè)問題,，本文采用速度補(bǔ)償?shù)姆绞剑谒俣刃蛄械哪┪蔡砑友a(bǔ)償速度序列來消除余數(shù)誤差,，得到的速度輸出序列X₅(h)如圖9所示,。

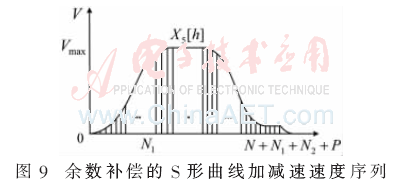
2.3 余數(shù)補(bǔ)償算法

    由于在通過FPGA實(shí)現(xiàn)的過程中采用定點(diǎn)數(shù)進(jìn)行計(jì)算，因此,，在卷積計(jì)算的除法運(yùn)算過程中,，需要考慮余數(shù)問題^[8]。事實(shí)上,，在整個(gè)數(shù)字卷積的計(jì)算中有兩種情況會產(chǎn)生余數(shù)：第一種情況是在數(shù)字卷積之前卷積序列長度N的計(jì)算,，如式(3)所示；另一種情況是在數(shù)字卷積計(jì)算過程中產(chǎn)生的余數(shù)如式(2)所示,。為了解決上述問題,，針對不同情況下的余數(shù)問題采用不同的算法來實(shí)現(xiàn)補(bǔ)償。

    對于在數(shù)字卷積之前產(chǎn)生的余數(shù),，余數(shù)R的計(jì)算如式(3)所示,，這種情況下采用在速度序列的末尾添加速度補(bǔ)償序列。梯形加減速的卷積序列X₂[N₁+N-1]如式(5)所示,，余數(shù)R可表示為：

    其中,，V是X₂[N₁+N-1]序列的值；A表示速度為V時(shí)的速度補(bǔ)償序列脈沖數(shù),；B表示最終補(bǔ)償脈沖序列的誤差值,。另外，P表示在圖7中總的添加的補(bǔ)償速度序列脈沖數(shù),。

    類似地,，對于S形曲線加減速速度序列X₄[N+N₁+N₂-1]如式(6)所示，余數(shù)R可以表示為：

    其中,，W是X₄[N+N₁+N₂-1]序列的值,；C表示速度為W時(shí)的速度補(bǔ)償序列脈沖數(shù)；D表示最終補(bǔ)償脈沖序列的誤差值,。另外,，P表示總的添加補(bǔ)償速度序列脈沖數(shù),。

3 仿真與驗(yàn)證分析

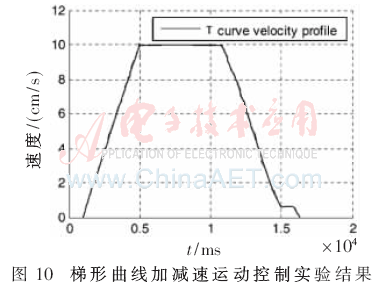
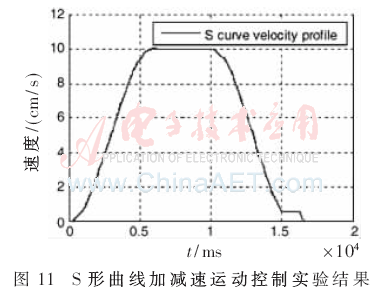
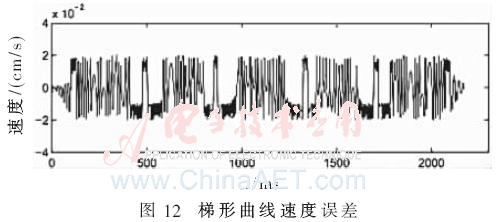
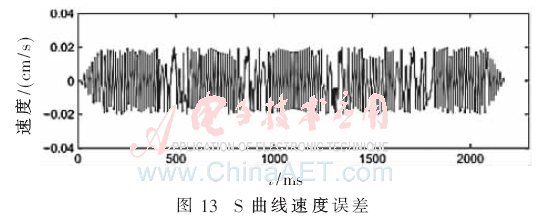
    仿真驗(yàn)證過程在Matlab和Quartus II 13.1開發(fā)環(huán)境下采用硬件描述語言Verilog,，在Altera的Cyclone IV器件上進(jìn)行仿真和驗(yàn)證實(shí)現(xiàn),。圖10為在MATLAB上S=250，V_max=10,，N₁=7時(shí)的梯形曲線加減速運(yùn)動控制實(shí)驗(yàn)結(jié)果,；圖11為S=250，V_max=10,，N₁=7,，N₂=4時(shí)的S形曲線加減速運(yùn)動控制實(shí)驗(yàn)結(jié)果；圖12,、圖13分別為梯形和S形曲線加減速速度誤差圖,，從圖中可以看出速度的誤差保持在±0.02范圍內(nèi)。圖14為S=250,，V_max=10,，N₁=7時(shí)的梯形曲線加減速通過FPGA硬件實(shí)現(xiàn)后在Modelsim上的仿真波形圖，圖15為S=250,，V_max=10,，N₁=7，N₂=4時(shí)的S形曲線加減速通過FPGA硬件實(shí)現(xiàn)后的仿真波形,，其中,，標(biāo)有圓圈部分為添加的余數(shù)補(bǔ)償速度部分。

4 結(jié)論

    針對工業(yè)機(jī)器人,、數(shù)控系統(tǒng)中的加減速控制算法引入了數(shù)字卷積,，減小了計(jì)算量，并通過FPGA硬件編程的方式實(shí)現(xiàn)了數(shù)字卷積的梯形曲線,、S形曲線加減速控制算法,。本文詳細(xì)分析了采用定點(diǎn)數(shù)計(jì)算數(shù)字卷積加減速算法過程的余數(shù)的處理方式。對與數(shù)字卷積運(yùn)算之前產(chǎn)生的余數(shù),，在速度序列的末尾添加速度補(bǔ)償序列來消除余數(shù)誤差,；對于數(shù)字卷積運(yùn)算過程中產(chǎn)生的余數(shù)，采用余數(shù)累加的方式,，來減小余數(shù)誤差,。采用FPGA硬件編程的方式實(shí)現(xiàn)加減速控制算法，簡化系統(tǒng)結(jié)構(gòu),，提高運(yùn)算效率和算法的穩(wěn)定性,。

參考文獻(xiàn)

[1] 鄭金興，張銘鈞.梯形速度控制變插補(bǔ)周期的實(shí)時(shí)插補(bǔ)算法研究[J].機(jī)床與液壓,，2007(1)：77-80.

[2] 朱明,，游有鵬，何均.S形加減速算法前瞻處理研究[J].小型微型計(jì)算機(jī)系統(tǒng),，2011(10)：2140-2144.

[3] 陳曉兵,，廖文和.基于分段刀軌S曲線加減速控制的進(jìn)給速度優(yōu)化研究[J].組合機(jī)床與自動化加工技術(shù),，2012(10)：44-47.

[4] 劉筱，吳文江,，鄭飂默.柔性S型加減速控制算法研究[J].組合機(jī)床與自動化加工技術(shù),，2014(3)：66-68.

[5] CHEN C S，LEE A C.Design of acceleration deceleration profiles in motion control based on digital FHR filters[J].Journal of Machine Tools & Manufacture,，2001,，38：799-825.

[6] KIM D I，JEON J W,，KIM S.Software acceleration/deceleration methods for industrial robots and cnc maching tools[J].Mechatronics,，1994，4(1)：37-53.

[7] 陳偉娜,，賴乙宗,，李松，等.數(shù)控系統(tǒng)線性加減速算法分析與實(shí)現(xiàn)[J].科學(xué)技術(shù)與工程,，2012(3)：546-550.

[8] 王昕,，王均偉，饒志,，等.基于NURBS曲線軌跡規(guī)劃與速度規(guī)劃的研究[J].系統(tǒng)仿真學(xué)報(bào),，2008(15)：3973-3980.