摘  要： PID控制器是過程控制中應(yīng)用最為廣泛的控制器，而傳統(tǒng)PID控制器參數(shù)整定難以達(dá)到最優(yōu)狀態(tài),，同時(shí),，存在控制結(jié)果超調(diào)量過大、調(diào)節(jié)時(shí)間偏長等缺點(diǎn),，因此,，將變異粒子群優(yōu)化算法（Mutation Particle Swarm Optimization，MPSO）運(yùn)用于BP-PID的參數(shù)整定過程中,，設(shè)計(jì)了一種高效,、穩(wěn)定的自適應(yīng)控制器?？紤]MPSO的變異機(jī)制,，以種群適應(yīng)度方差與種群最優(yōu)適應(yīng)度值為標(biāo)準(zhǔn)，進(jìn)行種群變異操作,，可以克服早熟，提高收斂精度和PSO的全局搜索能力,，使MPSO優(yōu)化的BP神經(jīng)網(wǎng)絡(luò)整定的PID控制器能以更快的速度,、更高的精度完成過程控制操作。在實(shí)驗(yàn)中,，通過比較BP-PID,、PSO-BP-PID以及MPSO-BP-PID三控制器仿真結(jié)果，證明了所提MPSO算法的有效性和所設(shè)計(jì)MPSO-BP-PID控制器的優(yōu)越性,。

　　關(guān)鍵詞： 變異粒子優(yōu)化算法,；BP神經(jīng)網(wǎng)絡(luò)；PID控制器,；MATLAB仿真

0 引言

　　PID控制即比例-積分-微分控制,，它是建立在經(jīng)典控制理論基礎(chǔ)上的一種控制策略。PID控制器具有算法簡單,、魯棒性強(qiáng),、穩(wěn)定可靠等優(yōu)點(diǎn)[1]。其中,，PID參數(shù)整定是PID控制器設(shè)計(jì)的關(guān)鍵所在[2-5],，而傳統(tǒng)的PID控制器參數(shù)整定主要通過人工經(jīng)驗(yàn)完成，不僅費(fèi)時(shí),，而且不能保證獲得最佳的控制效果,。在這種情況下，智能化算法[6-9]被引入到PID參數(shù)調(diào)整中,，其中神經(jīng)網(wǎng)絡(luò)[8]以其具有的非線性特性,、優(yōu)化和自適應(yīng)控制性能等被引入到PID控制器設(shè)計(jì)中,。但是在其實(shí)際應(yīng)用的過程中，采用BP神經(jīng)網(wǎng)絡(luò)所設(shè)計(jì)的BP-PID控制器時(shí),，由于其反向傳播學(xué)習(xí)算法的全局搜索能力弱,，易陷入局部最優(yōu)，其控制效果并不理想,，從而限制了神經(jīng)網(wǎng)絡(luò)在PID控制器中的應(yīng)用,。

　　針對(duì)上述問題，本文將變異操作引入粒子群算法,，形成變異粒子群算法,。以變異粒子群算法作為BP神經(jīng)網(wǎng)絡(luò)新的學(xué)習(xí)算法，設(shè)計(jì)了MPSO-BP-PID控制器,。該控制器不僅克服了粒子群算法最優(yōu)值搜索易陷入局部最優(yōu)值[8]以及BP神經(jīng)網(wǎng)絡(luò)反向傳播學(xué)習(xí)算法全局搜索能力弱的缺點(diǎn),，而且可以較大程度地提高其控制過程的穩(wěn)定性、精確性和魯棒性,。本文通過實(shí)驗(yàn)仿真,，建立了MPSO-BP-PID控制器，并在過程控制中與BP-PID,、PSO-PID控制器進(jìn)行對(duì)比,，結(jié)果證明MPSO-BP-PID控制器不僅在尋優(yōu)精度上，而且在尋優(yōu)速度上都比BP-PID和PSO-BP-PID控制器表現(xiàn)得更為優(yōu)異,。

1 MPSO-BP-PID控制器整體結(jié)構(gòu)

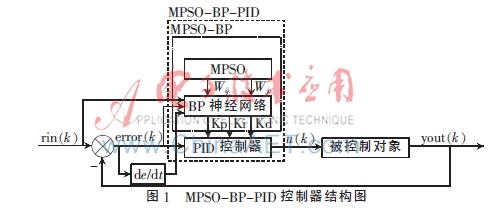
　　如圖1所示,，MPSO-BP-PID控制器由傳統(tǒng)PID控制器及MPSO優(yōu)化的BP神經(jīng)網(wǎng)絡(luò)組成。其中,，由MPSO優(yōu)化的BP神經(jīng)網(wǎng)絡(luò)部分稱為MPSO-BP,；而將MPSO-BP用到PID控制參數(shù)整定的部分稱為MPSO-BP-PID控制器。工作過程中,，利用系統(tǒng)輸入rin（k）和yout（k）之間的誤差信號(hào)error（k）,，同時(shí)根據(jù)某種性能指標(biāo)的最優(yōu)化，利用MPSO-BP在線實(shí)時(shí)調(diào)整PID控制器kp,，ki,，kd參數(shù)，得到PID調(diào)節(jié)器的輸出u（k）,，再根據(jù)控制對(duì)象的傳遞函數(shù)得到系統(tǒng)的輸出yout（k）,，從而實(shí)現(xiàn)直接對(duì)被控對(duì)象進(jìn)行閉環(huán)控制。

　　本文采用3層BP神經(jīng)網(wǎng)絡(luò)[10],，如圖2所示,，輸入層有3個(gè)神經(jīng)元即系統(tǒng)輸入rin（k），系統(tǒng)輸出yout（k）,，輸入與輸出之間的誤差error（k）,，輸入信號(hào)經(jīng)隱含層權(quán)值wij進(jìn)入隱含層,，隱含層有5個(gè)神經(jīng)元，隱含層輸出值乘以輸出層權(quán)值woj輸入輸出層,，輸出層有3個(gè)神經(jīng)元分別為kp,，ki，kd,。隱含層,、輸出層的激活函數(shù)fh，fo分別為式（1）和（2）[10]：

2 MPSO算法

　　2.1 PSO算法

　　粒子群算法（Particle Swarm Optimization,，PSO）是由Kennedy和Eberhart[11]博士在1995年提出的基于群智能的隨機(jī)優(yōu)化算法,，是模擬鳥類群體覓食行為的一種新的進(jìn)化計(jì)算方法。在D維搜索空間中,，第i個(gè)粒子在D維空間中的位置表示為：xi=（xi1,，xi2，xi3,，...xiD）,，第i個(gè)粒子經(jīng)歷的最好位置（個(gè)體最好適應(yīng)度）記為：pi=（pi1，pi2,，pi3,，...piD），在整個(gè)群體中,，所有粒子經(jīng)歷過的最好位置為：pg=（pg1，pg2,，pg3,，...pgD）。每個(gè)粒子的飛行速度為：vi=（vi1,，vi2,，vi3，...viD）,。每一代粒子根據(jù)式（3）和式（4）更新自己的速度和位置：

　　vid=wvid+c1r1（pid-xid）+c2r2（pgd-xid）（3）

　　xid=xid+vid（4）

　　其中：w為慣性權(quán)重[12],，慣性權(quán)重的引進(jìn)使PSO可以調(diào)節(jié)算法的全局與局部尋優(yōu)能力；c1和c2為正常數(shù),，稱為加速系數(shù),；r1和r2是[0，1]的隨機(jī)數(shù),。更新過程中,，粒子每一維的位置、速度都限制在允許的范圍之內(nèi),。

　　PSO算法結(jié)構(gòu)簡單,，搜索速度快,，同時(shí)也容易出現(xiàn)早熟現(xiàn)象，為了避免早熟對(duì)尋優(yōu)結(jié)果的影響,，保存?zhèn)€體的多樣性,，從而提高系統(tǒng)的全局搜索能力，在此引入變異操作,，使得粒子陷入局部最優(yōu)時(shí)能夠朝新的方向重新搜索,，增大尋找全局最優(yōu)的幾率，即為MPSO算法,。

　　2.2 MPSO算法

　　MPSO算法引入的變異操作[7]是以群體適度方差σ2和粒子數(shù)N為判斷標(biāo)準(zhǔn),，在人為設(shè)置的最大、最小變異概率之內(nèi),，群體適應(yīng)度方差越小,，即各粒子越靠近時(shí)，全局極值的變異概率越大,；反之,，當(dāng)適應(yīng)度方差越大即群體還保持較高的多樣性時(shí)，全局極值的變異概率越小,。具體粒子群變異操作的概率如式（5）：

　　其中：Pm為群體全局極值的變異概率,，σ2為群體適應(yīng)度方差，Pmax為變異概率的最大值,，Pmin為變異概率的最小值,。

　　考慮到粒子在當(dāng)前全局最佳適應(yīng)度f（gbest）的作用下可能找到更好位置，因此MPSO算法將變異操作設(shè)計(jì)成為一個(gè)隨機(jī)算子,，即對(duì)滿足變異條件的f（gbest）按一定的概率Pm進(jìn)行變異操作,。計(jì)算過程如式（6）：

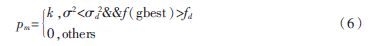
　　其中，k可以取[0.1,，0.2]之間的任意數(shù)值,。σ2的取值與實(shí)際問題有關(guān)，一般遠(yuǎn)小于σ2的最大值,，fd為理論最優(yōu)值,。在進(jìn)行粒子群尋優(yōu)的過程中，由于變異操作避免粒子群陷入一些偽最優(yōu)值,，從而使算法的全局搜索能力及魯棒性大大增強(qiáng),，從而更加容易發(fā)現(xiàn)目標(biāo)的全局最優(yōu)值。

3 MPSO-BP-PID控制器工作過程

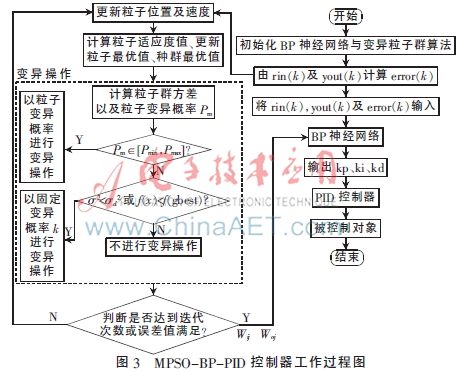
　　由圖3可知,，在MPSO-BP-PID控制器工作過程中,，第一步是由MPSO算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)。在此過程中MPSO算法結(jié)合PID控制對(duì)象的控制誤差error（k）對(duì)神經(jīng)網(wǎng)絡(luò)的隱含層權(quán)值wij及輸出層權(quán)值woj進(jìn)行優(yōu)化更新,，從而為BP神經(jīng)網(wǎng)絡(luò)提供優(yōu)化過的權(quán)值,，得到PID最優(yōu)化的控制參數(shù)kp,，ki，kd,；第二步,，在控制參數(shù)的作用下，由PID控制器輸出最優(yōu)化的控制參數(shù)u（k）,，從而完成最終對(duì)被控制對(duì)象的最優(yōu)控制,。

　　3.1 MPSO-BP-PID控制器

　　MPSO-BP-PID控制器具體執(zhí)行過程如下：

　　（1）初始化BP神經(jīng)網(wǎng)絡(luò)基本參數(shù),，確定網(wǎng)絡(luò)結(jié)構(gòu)以及節(jié)點(diǎn)數(shù),，并給出加權(quán)系數(shù)初始值；初始化粒子群算法中的基本參數(shù),，確定粒子速度與位置的范圍等,。

　　（2）由當(dāng)前輸入值rin（k）及被控制對(duì)象的傳遞函數(shù),，控制器輸出初始值計(jì)算當(dāng)前輸出yout（k）,，以及誤差函數(shù)error（k）=rin（k）-yout（k），得BP神經(jīng)網(wǎng)絡(luò)的輸入信號(hào)rin（k）,、yout（k）,、error（k），對(duì)輸入信號(hào)進(jìn)行采樣,、歸一化預(yù)處理,，之后輸入BP神經(jīng)網(wǎng)絡(luò)。

　?。?）正向計(jì)算BP神經(jīng)網(wǎng)絡(luò)各層神經(jīng)元輸入,、輸出，BP神經(jīng)網(wǎng)絡(luò)輸出的三個(gè)輸出值即為PID控制器的三個(gè)可調(diào)參數(shù)kp,，ki,，kd,。

　?。?）本文以增量式PID為例，由式（7）可得PID控制器的輸出為u（k）,，將得到的u（k）送入被控制系統(tǒng),，對(duì)被控制系統(tǒng)進(jìn)行在線調(diào)控。

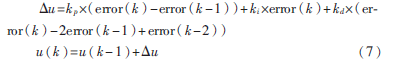
　　3.2 MPSO優(yōu)化BP神經(jīng)網(wǎng)絡(luò)

　　MPSO優(yōu)化BP神經(jīng)網(wǎng)絡(luò)具體過程如下：

　?。?）粒子群開始尋優(yōu),，將粒子的位置及速度向量都設(shè)計(jì)為隱含層和輸出層個(gè)數(shù)之和的維數(shù)M，其中N個(gè)粒子即為隱含層與輸出層權(quán)值wij,、woj可能的解,；

　?。?）根據(jù)公式（3）和公式（4），更新每個(gè)粒子的位置和速度,；

　?。?）由式（8）計(jì)算每個(gè)粒子的適應(yīng)度值，更新粒子個(gè)體最優(yōu)值及全局最優(yōu)值,；

　?。?）計(jì)算種群適應(yīng)度方差σ2，判斷種群適應(yīng)度方差及種群最優(yōu)適應(yīng)度值,，確定變異操作的概率,，如果Pm超出[Pmin，Pmax],，則以公式（6）進(jìn)行變異操作,，否則以公式（5）進(jìn)行變異操作；

　?。?）判斷迭代次數(shù)以及誤差值,，若滿足則終止迭代，則尋優(yōu)結(jié)束,，得到最優(yōu)粒子群即wij,、woj，將其送入BP神經(jīng)網(wǎng)絡(luò),，否則迭代次數(shù)加一返回步驟（2）,。

4 實(shí)驗(yàn)結(jié)果

　　將MPSO優(yōu)化的BP神經(jīng)網(wǎng)絡(luò)PID控制器應(yīng)用于非線性模型控制中，被控制對(duì)象模型如式（9）：

　　其輸入為指數(shù)衰減信號(hào),，如式（10）：

　　rin（k）=e-1.5×k×ts×sin（2π×k×ts）（10）

　　設(shè)種群大小為40,，迭代次數(shù)為10，粒子群慣性權(quán)重為[wmax,，wmin]=[0.9,，0.4]呈線性遞減，加速系數(shù)c1=c2=  1.496 2,，位置的初始范圍設(shè)置在[-1,，1]之間，速度的初始范圍設(shè)置在[-0.5,，0.5]之間,。BP神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)為：輸入層3個(gè)神經(jīng)元，隱含層5個(gè)神經(jīng)元,，輸出層3個(gè)神經(jīng)元,，神經(jīng)網(wǎng)絡(luò)的學(xué)習(xí)速率η=0.20，慣性系數(shù)α=0.05。輸入信號(hào)的采樣點(diǎn)數(shù)為6 000,，其采樣間隔為0.001,。圖4所示為BP-PID、PSO-BP-PID,、MPSO-BP-PID三種控制器的控制效果圖,，其中，在t=3.5 s時(shí)加入幅值為0.15的干擾量,。

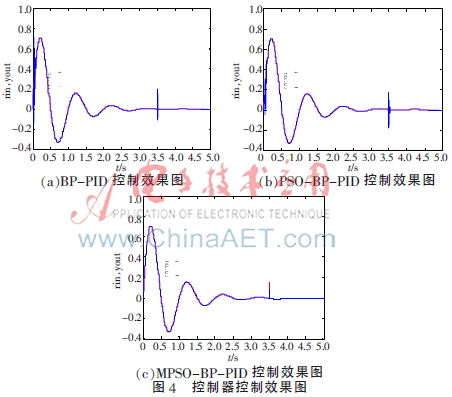
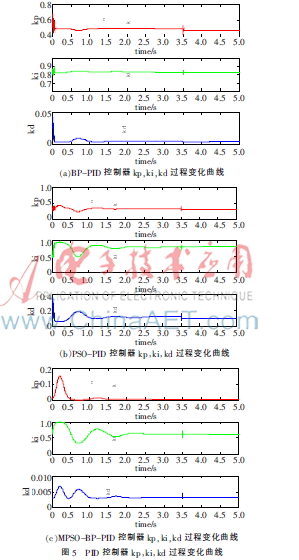
　　從圖4,、圖5可見，BP-PID,、PSO-BP-PID,、MPSO-BP-PID三種控制器對(duì)于被控制系統(tǒng)都起到了一定的控制作用。由控制器控制效果曲線圖以及kp,、ki,、kd過程變化曲線可知，控制器在初始階段都會(huì)產(chǎn)生誤差抖動(dòng),，其中,，BP-PID控制器初始階段中，誤差抖動(dòng)幅度較大且持續(xù)時(shí)間較長,，相比于BP-PID控制器誤差抖動(dòng),，PSO-BP-PID控制器初始階段誤差抖動(dòng)幅度與抖動(dòng)所持續(xù)的時(shí)間都有所減小。而MPSO-BP-PID控制器在初始階段的調(diào)整中不論在調(diào)整幅度還是在調(diào)整時(shí)間等方面相比BP-PID和PSO-BP-PID控制器都有更好的控制效果,。

　　在t=3.5 s加入突變式干擾量時(shí),，三種控制器都能對(duì)外界干擾做出反應(yīng)。其中,，BP-PID控制器反應(yīng)速度較慢,，且調(diào)整過程存在的誤差抖動(dòng)幅度較大；相比于BP-PID控制器,，PSO-BP-PID控制器也同樣存在著反應(yīng)時(shí)間長,、所持續(xù)的誤差抖動(dòng)較大的問題。而MPSO控制器對(duì)于干擾的反應(yīng)速度較于BP-PID控制器和PSO-BP-PID控制器快,，且調(diào)整幅度小,，過渡時(shí)間短，這將有利于MPSO-BP-PID控制器在復(fù)雜壞境情況下對(duì)于被控制對(duì)象的實(shí)時(shí)控制,。

　　導(dǎo)致上述控制效果的主要原因：BP-PID控制器以傳統(tǒng)的誤差反向傳播的BP算法為學(xué)習(xí)算法,，然而BP算法的全局搜索能力弱且易陷入局部最優(yōu)值與偽最優(yōu)值,，因此控制效果并不理想,，對(duì)于突變式干擾，通常會(huì)有較大的誤差抖動(dòng),；而以PSO優(yōu)化算法為學(xué)習(xí)算法的PSO-BP-PID控制器雖然操作簡單,，方便易行,，并且在一定程度上克服了BP算法易陷入局部最優(yōu)值的問題，但在算法優(yōu)化后期也存在著優(yōu)化速度降低以及早熟等情況,，導(dǎo)致其全局搜索能力減弱而不繼續(xù)優(yōu)化以獲得最優(yōu)值,，因此，其控制效果欠佳,，對(duì)于突變式干擾的適應(yīng)性較差并且導(dǎo)致個(gè)別區(qū)域誤差比較大,；MPSO-BP-PID控制器則采用具有變異能力的MPSO優(yōu)化算法，與PSO算法相比較,，MPSO優(yōu)化算法考慮到粒子多樣性對(duì)尋優(yōu)的有利影響,，在PSO的基本框架中增加了由種群適應(yīng)度方差以及粒子數(shù)確定的隨機(jī)變異算子和通過對(duì)最優(yōu)適應(yīng)度值的判斷而確定固定變異算子來提高粒子群跳出局部最優(yōu)解的能力且增加粒子群的多樣性，從而在PSO優(yōu)化算法后期,，跳出其中偽最優(yōu)值與次優(yōu)解,，繼而克服了PSO算法自身所具有的早熟問題，使其全局搜索能力增強(qiáng),，算法的魯棒性也得到了較大提高,，從而確保PID控制完成對(duì)被控制對(duì)象的精確控制。因此,，MPSO-BP-PID控制器能在較大程度上提高其控制過程的穩(wěn)定性,、精確性與魯棒性。

5 結(jié)論

　　本文提出了一種新的改進(jìn)粒子群算法,，即變異粒子群算法,，用于優(yōu)化BP神經(jīng)網(wǎng)絡(luò)權(quán)值，從而建立了MPSO-BP-PID控制器,。由于MPSO優(yōu)化算法引入變異的概念,，在粒子群尋優(yōu)過程中，使其具有更強(qiáng)的全局及局部尋優(yōu)能力,，該算法在增加種群多樣性的同時(shí)也有效地克服了傳統(tǒng)PSO易陷入局部最優(yōu)的缺點(diǎn),，充分發(fā)揮了PSO種群間搜索信息的能力，從而保證其在尋優(yōu)權(quán)值時(shí)能得到最優(yōu)權(quán)值,，縮短了BP神經(jīng)網(wǎng)絡(luò)的訓(xùn)練時(shí)間,，同時(shí)使BP-PID控制器在初始階段，能更有效果地跟蹤系統(tǒng)整體變化,，在快速應(yīng)變方面有著更為優(yōu)秀的表現(xiàn),。仿真結(jié)果表明，基于MPSO-BP-PID控制器可以實(shí)現(xiàn)對(duì)被控系統(tǒng)的有效控制,，并使相應(yīng)控制過程的穩(wěn)定性,、精確性與魯棒性都有較大的提高。

參考文獻(xiàn)

　　[1] VILANOVA R， ALFARO V. Robust PID control： an overview[J]. Revista Iberoamericana De Automatica E Informatica Industrial,， 2011,， 8（3）：141-158.

　　[2] Zhang Jinhua， Zhuang Jian,， Du Haifeng,， et al. Self-organizing genetic algorithm based tuning of PID controllers[J]. Information Sciences， 2009,，179（7）：1007-1018.

　　[3] NTOGRAMATZIDIS L,， FERRANTE A. Exact tuning of controllers in control feedback design[J]. IET Control Theory And Applications， 2011,， 5（4）： 565-578.

　　[4] 王偉,，張晶濤，柴天佑.PID參數(shù)先進(jìn)整定方法綜述[J].自動(dòng)化學(xué)報(bào),，2000,，26（3）：347-355.

　　[5] 霍延軍.基于量子粒子群算法的PID參數(shù)自整定方法[J].微電子學(xué)與計(jì)算機(jī)，2012,，20（10）：194-197.

　　[6] NTOGRAMATZIDIS L,， FERRANTE A. Exact tuning of controllers in control feedback design[J]. IET Control Theory and Applications， 2011,， 5（4）： 565-578.

　　[7] HSU C F,， TSAI J Z， CHIU C J. Chaos synchronization of nonlinear gyros using self-learning PID control approach[J]. Applied Soft Computing,， 2012,， 12（1）： 430-439.

　　[8] SENG T L， BIN K,， YUSOF R. Tuning of a neuro-fuzzy controller by genetic algorithm[J]. IEEE Transactions on Systems,， Man， and Cybernetics,， 1999,，29（2）：226-236.

　　[9] MOHAN B M. Fuzzy PID control via modified takagi-sugeno rules[J]. Intelligent Automation and Soft Computing， 2011,， 17（2）： 165-174.

　　[10] 劉金琨.先進(jìn)PID控制MATLAB仿真[M].北京：電子工業(yè)出版社,，2004.

　　[11] KENNEDY J， EBERHART R. Particle swarm optimization[C]. Proceedings of the 1995 IEEE International Conference on neural networks,， 1995： 1942-1948.

　　[12] SHI Y,， EBERHART R C. Particle swarm optimization： developments， applications and resources[C]. Proceedings of the IEEE Congress on Evolutionary Computation,， 2001：81-86.