摘  要： 對(duì)流層延遲與對(duì)流層的折射率有關(guān)，且隨著衛(wèi)星仰角的減小而增加,，在衛(wèi)星仰角為5°時(shí)會(huì)產(chǎn)生25 m左右的誤差,，給GPS導(dǎo)航定位帶來不利的影響。系統(tǒng)地分析了對(duì)流層延遲特性并對(duì)常用的誤差修正模型進(jìn)行了比較,?；?a class="innerlink" href="http://forexkbc.com/tags/Saastamoinen模型" title="Saastamoinen模型" target="_blank">Saastamoinen模型提出了一種簡易的對(duì)流層延遲修正模型，該模型不需測(cè)量氣象參數(shù),，且實(shí)驗(yàn)結(jié)果表明,，簡易修正模型可以很好地消除對(duì)流層影響，有效地提高了GPS導(dǎo)航定位系統(tǒng)的精度,。

　　關(guān)鍵詞： 對(duì)流層延遲,；GPS；修正模型

0 引言

　　全球定位系統(tǒng)（Navigation Satellite Timing And Ranging Global Position System,，GPS）由32顆衛(wèi)星組成,，可以為全球GPS用戶提供全天候的連續(xù)的三維坐標(biāo)位置、速度以及時(shí)間信息[1-3],。

　　對(duì)流層是離地面高度50 km以下的大氣層,，包括對(duì)流層和平流層。GPS穿過對(duì)流層和平流層時(shí),，其傳播速度將發(fā)生變化,，傳播路徑將發(fā)生彎曲，從而產(chǎn)生額外的路徑延遲,，稱為對(duì)流層延遲,。對(duì)流層延遲與信號(hào)的工作頻率有關(guān)，研究表明,，對(duì)于15 GHz以內(nèi)的微波信號(hào),，其延遲可以忽略不計(jì)，但是對(duì)于工作在1 227.6 MHz和  1 575.42 MHz的GPS信號(hào)而言,，即使當(dāng)GPS在天頂方向運(yùn)行時(shí),，由對(duì)流層引起的偏差也可以達(dá)到2~3 m。

　　目前常用的對(duì)流層延遲修正模型有Hopfield模型,、Saastamoinen模型以及它們的改進(jìn)模型[4-6],。本文在分析對(duì)流層延遲特性的基礎(chǔ)上，提出了一種簡易的對(duì)流層修正模型,，該模型不需要測(cè)量觀測(cè)站的氣象參數(shù),，且實(shí)驗(yàn)結(jié)果表明，該模型能很好地消除對(duì)流層延遲誤差的影響,，可以有效地提高GPS系統(tǒng)的導(dǎo)航定位精度,。

1 對(duì)流層延遲分析

　　對(duì)流層引起的額外路徑延遲是GPS信號(hào)的實(shí)際傳播距離S與幾何路徑ρ之差，如圖1所示,。

　　若用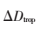表示對(duì)流層延遲,，則：

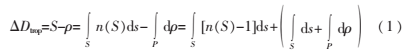
　　其中，n（S）表示對(duì)流層折射率,。上式右端第一項(xiàng)為信號(hào)速度變化引起的延遲,，其對(duì)應(yīng)的時(shí)間稱為對(duì)流層時(shí)延；第二項(xiàng)是對(duì)流層導(dǎo)致的GPS信號(hào)傳播路徑彎曲,，其值為毫米級(jí),，可以忽略不計(jì)。

　　對(duì)于波長很短的電磁波來說,，對(duì)流層有色散效應(yīng),，此時(shí)可以利用雙頻測(cè)距儀來消除對(duì)流層延遲。但是GPS信號(hào)波長很長,，不存在色散效應(yīng),，因此只能通過計(jì)算式（1）積分來計(jì)算對(duì)流層延遲，即需要求出傳播路徑上各處的大氣折射系數(shù)N,。令：

　　N=（n-1）×106（2）

　　其中,，N為大氣折射系數(shù)，與氣體溫度和氣壓有關(guān),。80%以上的對(duì)流層延遲是由大氣中的干燥氣體引起的,，稱為干分量，其余延遲是由水蒸氣引起的,，稱為濕分量,，其折射系數(shù)分別用Nd、Nw,，表示,，則：

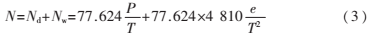
　　其中，P,、T,、e為大氣壓力（mbar）、溫度（K）和水汽分壓（mbar）,。由式（3）可知,，若要求解對(duì)流層延遲，則需要求出GPS信號(hào)傳播路徑上各處的大氣壓力,、溫度以及水汽分壓,，這是不現(xiàn)實(shí)的，因此必須建立適當(dāng)?shù)哪Ｐ蛠斫魄蟮脤?duì)流層延遲,。

2 常用對(duì)流層延遲修正模型

　　常用的對(duì)流層延遲修正模型有Hopfield模型和Saastamoinen模型,，這些模型在一定情況下可以有效地修正對(duì)流層延遲,，但是在觀測(cè)站環(huán)境條件變化時(shí)會(huì)產(chǎn)生很大的偏差。

　　2.1 Hopfield模型

　　該模型是Hopfield在1969年根據(jù)實(shí)測(cè)數(shù)據(jù)得到的,，該模型假設(shè)大氣溫度下降率為一常數(shù)：

　　即觀測(cè)站高程每升高1 km,，溫度就下降6.8℃。其天頂方向干延遲δdz和濕延遲δwz經(jīng)驗(yàn)公式分別為：

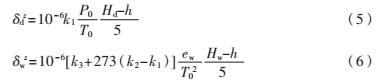
　　其中,，P0,、T0、ew,、Hd,、Hw和h分別為地面氣壓（mbar）、地面溫度（K）,、觀測(cè)站水汽壓（mbar）,、干大氣層頂高、濕大氣層頂高和測(cè)站在大地水準(zhǔn)面上的高度（m）,；k1,、k2、k3為常參數(shù),，它們的經(jīng)驗(yàn)值可取為：k1=77.6 K/mbar,，k2=71.6 K2/mbar，k3=3.747×105 K2/mbar,。

　　Hd=40 136+148.72（T0-273.16）（7）

　　Hw=11 000 m（8）

　　將式（7）和式（8）以及k1,、k2、k3帶入式（5）和式（6）可以得到對(duì)流層天頂干延遲和濕延遲：

　　2.2 Saastamoinen模型

　　該模型也是針對(duì)觀測(cè)站天頂方向的對(duì)流層延遲進(jìn)行修正,，其干分量和濕分量延遲分別為：

　　δdz=0.002 277×P（11）

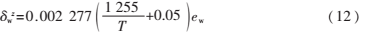
　　式中各符號(hào)的含義與Hopfield模型一致,，如果考慮觀測(cè)站的位置，則總的對(duì)流層延遲可以表示為：

　　其中,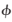，為觀測(cè)站緯度,，h為觀測(cè)站高程，P為高程h處的氣壓,。

　　由于上述兩種模型僅能對(duì)觀測(cè)站天頂方向的對(duì)流層延遲進(jìn)行修正,，因此限制了其適用范圍，對(duì)位置快速變化的高超聲速飛行器并不適用,。

3 Saastamoinen簡易模型

　　飛行器以高超聲速在空間進(jìn)行飛行時(shí),，其與GPS導(dǎo)航衛(wèi)星之間的相對(duì)位置在不斷地變化，因此衛(wèi)星的仰角也在不斷變化,。此時(shí)如果僅對(duì)GPS信號(hào)天頂方向的對(duì)流層延遲進(jìn)行修正,，肯定會(huì)給導(dǎo)航定位帶來很大的誤差，所以迫切需要建立與觀測(cè)站位置也即飛行器位置有關(guān)同時(shí)能適應(yīng)不同GPS仰角的對(duì)流層延遲修正模型。

　　在對(duì)Saastamoinen模型進(jìn)行修正后,，可以得到如下模型：

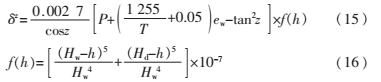
　　其中,，f（h）為高程修正函數(shù)，z是衛(wèi)星的天頂距,，其余符號(hào)含義與Hopfield模型相同,。在獲得飛行器高程及環(huán)境參數(shù)后，根據(jù)該簡易模型便可求出參與導(dǎo)航定位的任意仰角的GPS信號(hào)的對(duì)流層延遲,。

4 模型對(duì)比

　　4.1 模型參數(shù)選擇

　　上述三種模型的參數(shù)均可以離線得到，對(duì)于氣壓和溫度P0,、T0,，可以取海平面標(biāo)準(zhǔn)氣壓和溫度為參考值，即P0=1 013.25 mbar,，T0=291.16 K,。

　　高程h處大氣的溫度、大氣壓力,、水蒸氣壓力分別為：

　　T=T0-0.006 5×h（17）

　　P=P0×（1-0.000 226×h）2（18）

　　ew=RH×exp（-37.246 5+0.213 166T-0.000 256 908T2）（19）

　　其中,，RH=RH0×exp（-0.000 639 6×h），RH0=50%,。

　　圖2給出了文中三種模型在天頂方向上對(duì)對(duì)流層延遲的修正效果隨觀測(cè)站高程變化的曲線,，對(duì)于Saastamoinen模型，取觀測(cè)站緯度為南京新街口地理緯度32°02′,。

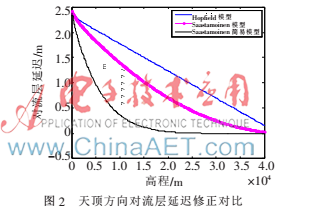
　　由圖2可以看出,，衛(wèi)星對(duì)流層延遲隨高程的增加而不斷減小，當(dāng)觀測(cè)站高程為0 m時(shí)對(duì)流層延遲可達(dá)到2.5 m,，在高程為40 km時(shí)對(duì)流層延遲幾乎可以忽略不計(jì),。

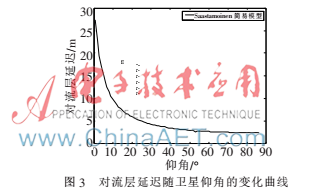
　　GPS衛(wèi)星仰角大于15°時(shí)即為可見衛(wèi)星，因此若高超聲速飛行器捕獲到此顆信號(hào),，該衛(wèi)星便可與其他衛(wèi)星一起對(duì)飛行器進(jìn)行導(dǎo)航定位,。圖3給出了觀測(cè)站高程為0 m時(shí)，簡易模型對(duì)對(duì)流層延遲的修正效果隨衛(wèi)星仰角變化的曲線,?？梢钥闯觯谛l(wèi)星仰角小于30°時(shí),，對(duì)流層延遲隨衛(wèi)星仰角的增加而急劇下降,。在衛(wèi)星仰角等于5°左右時(shí)，對(duì)流層延遲可以達(dá)到25 m,，與參考文獻(xiàn)[6]數(shù)據(jù)一致,。當(dāng)衛(wèi)星仰角增加到30°左右時(shí)，對(duì)流層延遲減小到5 m左右,，此后隨著衛(wèi)星仰角的增加,，對(duì)流層延遲緩慢減小,。

　　4.2 高超聲速實(shí)驗(yàn)驗(yàn)證

　　為了驗(yàn)證采用簡易模型對(duì)對(duì)流層延遲的修正效果，本文進(jìn)行了高超聲速實(shí)驗(yàn)驗(yàn)證,，飛行器的飛行速度設(shè)為10馬赫,。由于飛行器的速度非常快,，其定位誤差自然會(huì)很大,，因此本文采用卡爾曼濾波分別對(duì)跟蹤結(jié)果和定位結(jié)果進(jìn)行處理，在進(jìn)一步減小定位誤差的基礎(chǔ)上分析簡易模型對(duì)對(duì)流層延遲修正的效果,。為了對(duì)高超聲速飛行器進(jìn)行實(shí)時(shí)的導(dǎo)航定位,，仿真時(shí)每隔0.1 s便更新一次飛行器位置，仿真總時(shí)間為25 s,。仿真結(jié)果給出了高超聲速飛行器在地球坐標(biāo)系中三個(gè)坐標(biāo)分量的誤差,，分別如圖4、圖5和圖6所示,。

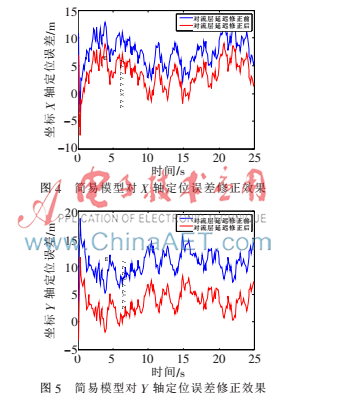
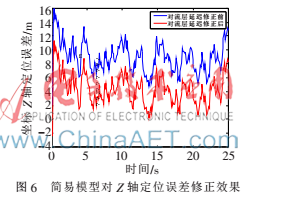
　　可以看出,，模型修正后，各坐標(biāo)軸的定位誤差都有所減小,。其中圖4中定位誤差由均值7.6 m修正為3.7 m,，圖5中定位誤差由均值10.7 m減小到3.7 m，圖6中定位誤差由均值8.9 m減小到4.4 m,，可見修正效果接近70%,，因此大大提高了GPS導(dǎo)航衛(wèi)星對(duì)高超聲速飛行器的定位精度。

5 結(jié)論

　　本文提出了一種簡易的對(duì)流層延遲修正模型,，該模型不需要實(shí)時(shí)測(cè)量目標(biāo)站的氣象參數(shù),，僅根據(jù)目標(biāo)站的高程以及可見GPS導(dǎo)航衛(wèi)星仰角就能對(duì)對(duì)流層延遲誤差進(jìn)行估計(jì)，通過高超聲速飛行器仿真實(shí)驗(yàn)可以看出,，本文的簡易對(duì)流層延遲模型可以很好地修正對(duì)流層延遲誤差,，且效果達(dá)到70%左右，大大提高了GPS導(dǎo)航衛(wèi)星的定位精度,，這對(duì)高動(dòng)態(tài)飛行器的導(dǎo)航定位是難能可貴的,。

參考文獻(xiàn)

　　[1] 唐學(xué)術(shù).高動(dòng)態(tài)GPS接收機(jī)的捕獲與跟蹤算法研究[D].北京：北京理工大學(xué)，2008.

　　[2] 游廣芝.GPS導(dǎo)航定位中的誤差分析與修正[D].哈爾濱：哈爾濱工業(yè)大學(xué),，2007.

　　[3] 龔真春,，陳安寧，李平,，等.GPS動(dòng)態(tài)定位中自適應(yīng)卡爾曼濾波方法的應(yīng)用研究[J].測(cè)繪通報(bào),，2006（7）：9-12.

　　[4] PARKINSON B W， SPIKLER J J. Global positioning system： theory and application[M]. American Institute of Astronautics and Aeronautics， 1996.

　　[5] SAASTAMOINEN J. Contributions to the theory of atmospheric refraction[J]. Bulletin Géodésique,， 1972,， 105（1）：279-298.

　　[6] ALTSHULER E E. Tropospheric range-error corrections for the global positioning system[J]. IEEE Transactions on Antennas & Propagation， 1998,， 46（5）：643-649.