0 引言

    由于成像環(huán)境不理想以及成像設(shè)備硬件分辨率有限等多種因素會(huì)導(dǎo)致圖像出現(xiàn)模糊,、噪聲等問(wèn)題,，導(dǎo)致獲取不到超分辨率圖像^[1]。故學(xué)者們提出了多幀超分辨率圖像重構(gòu)方法,，利用低分辨率圖像序列間某種類(lèi)別的附加信息進(jìn)行互補(bǔ)重構(gòu),，獲取無(wú)法辨識(shí)的細(xì)節(jié)信息從而轉(zhuǎn)換成高分辨率圖像^[2-3]。

    基于學(xué)習(xí)以及基于插值技術(shù)的重構(gòu)方法為目前較常用的超分辨率圖像重構(gòu)方法,。如Ahmadreza^[4]等人利用各向同性高斯濾波器,，對(duì)輸入圖像像素的結(jié)構(gòu)張量進(jìn)行計(jì)算，再利用結(jié)構(gòu)張量插值法實(shí)現(xiàn)重構(gòu),，實(shí)驗(yàn)表明該方法能獲得質(zhì)量較高的重構(gòu)圖像,。賈茜^[5]等人通過(guò)輪廓模板插值算法對(duì)低分辨率圖像進(jìn)行放大，然后將所得圖像用MCA模型分解,，最后將處理后的圖像進(jìn)行合成,，從而完成超分辨率圖像重構(gòu)。實(shí)驗(yàn)結(jié)果表明該方法有效提高了圖像銳度,，重構(gòu)效果佳,。雖然基于插值法的重構(gòu)算法實(shí)現(xiàn)快速易行，對(duì)超分辨率圖像重構(gòu)也有一定的效果,，但由于插值過(guò)程所固有的平滑效應(yīng),，導(dǎo)致得到的重構(gòu)圖像存在棋盤(pán)和振鈴效應(yīng)。

    對(duì)此,，樊博^[6]等人利用兩步迭代算法和全變分正則化實(shí)現(xiàn)超分辨率圖像重構(gòu),，利用兩步迭代收縮得到新的估值，最后利用全變分實(shí)現(xiàn)重構(gòu),，實(shí)驗(yàn)表明該算法能夠較好地實(shí)現(xiàn)圖像的重構(gòu),。首照宇^[7]提出了一種改進(jìn)的基于字典的重構(gòu)算法，通過(guò)引入聯(lián)合訓(xùn)練思想確保高,、低分辨率圖像具有相同的表示系數(shù),，利用迭代反投影增強(qiáng)重建約束實(shí)現(xiàn)重構(gòu)，實(shí)驗(yàn)結(jié)果顯示該方法具有較好的重構(gòu)效果,。

    然而,，此類(lèi)算法都是基于學(xué)習(xí)的超分辨率方法，在重構(gòu)效果上較插值法都有所提高,，但是由于計(jì)算的復(fù)雜性導(dǎo)致該類(lèi)方法實(shí)現(xiàn)復(fù)雜,，效率較低。

    對(duì)此，本文提出了增益映射控制耦合局部正則化的圖像重構(gòu)算法,。首先,，通過(guò)對(duì)低分辨率圖像中亞像素的移動(dòng)進(jìn)行分析；然后,，構(gòu)造正則化算子,，聯(lián)合改進(jìn)的代數(shù)重建法求其穩(wěn)定值；最后,，采用基于局部自適應(yīng)正則化的增益可控方法,，建立增益映射，完成超分辨率圖像重構(gòu),，并測(cè)試本文算法的重構(gòu)性能,。

1 圖像成像模型

    由于拍攝時(shí)相機(jī)的移動(dòng)等原因會(huì)導(dǎo)致亞像素平移的產(chǎn)生，從而使圖像變得不清晰^[8-9],。圖1中表示了低分辨率圖像[β_x,，β_y]中覆蓋3個(gè)亞像素沿水平和垂直方向平移的示意圖。

2 超分辨率圖像的估值

    因?yàn)榉匠淌浇M式(10)存在病態(tài)特性,，所以式(10)是不穩(wěn)定的，下面將對(duì)方程式組式(10)進(jìn)行求解,。

3 迭代算法與正則化

    代數(shù)重建法(ART)屬于級(jí)數(shù)展開(kāi)法的一種并得到了廣泛應(yīng)用^[10],。ART利用L₂范制定了相異度，并且對(duì)迭代后得到的每一個(gè)元素都進(jìn)行了更新,。由于在進(jìn)行誤差估值時(shí)L₁范比L₂范有更好的效果,，在此將ART中的相異度改進(jìn)為用L₁范來(lái)制定，那么中第j個(gè)元素的第(n+1)次迭代的表達(dá)式如下：

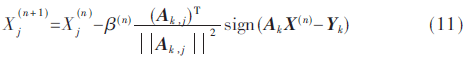
其中j=0,，1,，2…N-1，k=0,，1,，2，…K-1,，A_k,，j是A_k中的第j列元素。迭代參數(shù)β⁽ⁿ⁾表示第n次迭代的步長(zhǎng),。其中迭代次數(shù)n與低分辨率圖像指數(shù)k有關(guān),，其關(guān)系為n=k/K。

    正則化被廣泛用在求解不穩(wěn)定線性方程組上,，當(dāng)獲得數(shù)據(jù)的保真度很低時(shí),，正則化過(guò)程很重要^[11-13]。由于式(10)的不穩(wěn)定性導(dǎo)致高清圖像X的重構(gòu)存在不穩(wěn)定性，所以本文將用正則化耦合L₁范的ART來(lái)得到改進(jìn)的ART,，從而求解式(10)的穩(wěn)定解,。

    一個(gè)獲得圖像重構(gòu)穩(wěn)定解的方法是保持圖像空間灰度的同質(zhì)性^[14-15]。為了獲取該穩(wěn)定解,，本文構(gòu)造一個(gè)正則化算子φ(X),，根據(jù)高清圖像解法的先驗(yàn)知識(shí)，可將正則化算子φ(X)與式(8)結(jié)合,，可得到廣義的最小代價(jià)函數(shù)：

    由圖2可見(jiàn),，通過(guò)正則化耦合的ART算法迭代后所得圖像雖然有一定的重構(gòu)效果，但是還存在明顯的振鈴以及模糊效應(yīng),。下面將采用局部自適應(yīng)正則化的增益可控方法,，建立增益映射，完成超分辨率圖像重構(gòu),。

4 局部自適應(yīng)正則化及增益映射的建立

    由于邊緣高對(duì)比度及振鈴大小與圖像梯度大小成正比,，故本文采用自適應(yīng)技術(shù)，使得被估計(jì)的高清圖像中,，每個(gè)像素值的正則項(xiàng)和誤差項(xiàng)的關(guān)系由該像素值的局部信息來(lái)控制,，從而克服振鈴效應(yīng)和模糊效應(yīng)。本文采用基于局部自適應(yīng)正則化的增益可控方法,，建立增益映射,，完成超分辨率圖像重構(gòu)。

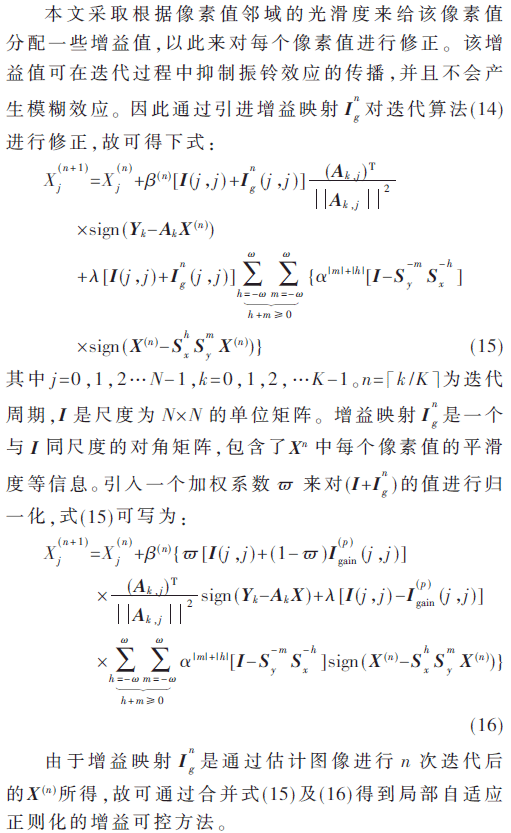
    膨脹-腐蝕現(xiàn)象影響了原始圖像的邊緣強(qiáng)度,，其中圖像的膨脹會(huì)帶來(lái)白噪聲的影響,，圖像的腐蝕會(huì)帶來(lái)暗噪聲的影響。然而形態(tài)學(xué)開(kāi)運(yùn)算和閉運(yùn)算,，能夠在不影響圖像邊緣銳度的情況下分別移除白噪聲和暗噪聲^[16-17],。故在此將構(gòu)造基于增益映射I_g的多尺度形態(tài)學(xué)。假設(shè)Q表示一個(gè)圓盤(pán)結(jié)構(gòu)元素單元,，則rQ定義如下：

其中Z_max和Z_min為Z的最大和最小值,，Sigmoid為一個(gè)邏輯函數(shù)，定義如下：

    (4)通過(guò)對(duì)Z的像素字典進(jìn)行排序,，獲取對(duì)角元素,，從而形成增益映射I_g。

    結(jié)構(gòu)元素大小的最大值m由估值圖像的對(duì)比度決定,，隨著迭代的進(jìn)行,，m將逐漸減少。

    圖3展示了本文算法的重構(gòu)效果對(duì)比圖,，在此m的取值為4,，圖3(a)為本文算法迭代1次后所得圖像，(b)為本文算法迭代10次后所得圖像。

5 仿真結(jié)果與分析

    采用經(jīng)過(guò)模糊后的圖像作為低分辨率圖像,，模糊算子H采用5×5的加權(quán)系數(shù),，再將下采樣因子D為5的噪聲加入目標(biāo)圖像，最后所得被損壞圖像為彩色圖像和灰度圖像作為測(cè)試圖像,，見(jiàn)圖4（a）,、圖5（a）。通過(guò)借助MATLAB 7.10軟件來(lái)測(cè)試本文超分辨率圖像重構(gòu)機(jī)制,，為了體現(xiàn)本文機(jī)制有效性與優(yōu)異性,，將文獻(xiàn)[18]和文獻(xiàn)[19]的重構(gòu)方法作對(duì)照。

5.1 不同機(jī)制對(duì)彩色圖像重構(gòu)的質(zhì)量對(duì)比分析

    圖4為不同圖像重構(gòu)機(jī)制對(duì)圖4（a）重構(gòu)后的效果圖,?？梢?jiàn)在對(duì)低分辨率彩色圖像重構(gòu)時(shí)，本文機(jī)制的重構(gòu)質(zhì)量最佳,，見(jiàn)圖4（d）,；而對(duì)照組的兩種圖像重構(gòu)算法重構(gòu)的圖像顯然存在振鈴和模糊效應(yīng)，見(jiàn)圖4（b）和圖4（c）,。原因是本文重構(gòu)機(jī)制采用自適應(yīng)技術(shù),，使得被估計(jì)的高清圖像中，每個(gè)像素值的正則項(xiàng)和誤差項(xiàng)的關(guān)系由該像素值的局部信息來(lái)控制,，從而克服振鈴效應(yīng)和模糊效應(yīng),。

5.2 不同機(jī)制對(duì)灰色圖像重構(gòu)的質(zhì)量對(duì)比

    從視覺(jué)效果圖對(duì)比可見(jiàn)，在對(duì)低分辨率灰色圖像重構(gòu)時(shí),，本文機(jī)制的重構(gòu)質(zhì)量最佳,，見(jiàn)圖5（d）,，圖像清晰度較好,；而對(duì)照組的兩種圖像重構(gòu)算法的復(fù)原圖像質(zhì)量不佳，分別見(jiàn)圖5（b）與圖5（c）,，較為模糊,，喪失了部分紋理信息。

5.3 量化分析

    將不同程度的噪聲加入到圖4的低分率圖像中,，然后用不同重構(gòu)算法來(lái)處理這些圖像,，最后通過(guò)得到的PSNR來(lái)對(duì)不同機(jī)制的重構(gòu)效果進(jìn)行量化分析，PSNR量化圖如圖6所示,。從圖中可見(jiàn),，本文重構(gòu)機(jī)制優(yōu)于對(duì)照組的機(jī)制，原因是本文采用了基于增益映射I_g的多尺度形態(tài)學(xué),，能夠在不影響圖像邊緣銳度的情況下分別移除白噪聲和暗噪聲,，從而保持了邊緣銳度提高了PSNR，保持了圖像的結(jié)構(gòu)相似度。

6 結(jié)論

    本文提出了基于局部自適應(yīng)正則化的圖像重構(gòu)算法,。通過(guò)對(duì)低分辨率圖像中亞像素的移動(dòng)進(jìn)行分析,，確定高低分辨率圖像間的形成模型, 將重構(gòu)問(wèn)題轉(zhuǎn)化為一個(gè)不穩(wěn)定的線性方程式組；然后構(gòu)造正則化算子,，聯(lián)合改進(jìn)的代數(shù)重建法求其穩(wěn)定值,；最后采用基于局部自適應(yīng)正則化的增益可控方法，完成超分辨率圖像重構(gòu),。仿真結(jié)果表明,，本文機(jī)制擁有更好的重構(gòu)效果，有效降低了模糊與振鈴效應(yīng),。

參考文獻(xiàn)

[1] CHENG P,，QIU Y Y，ZHAO K,，et al.A transductive graphical model for single image super-resolution[J].Elsevier Neurocomputing,，2015，148(1)：376-387.

[2] POLATKAN G,，BLEI D,，DAUBECHIES I.A bayesian nonparametric approach to image super-resolution[J].Pattern Analysis and Machine Intelligence，2015,，37(2)：346-358.

[3] ROYLE S J.Super-duper resolution imaging of mitotic microtubules[J].Nature Reviews Molecular Cell Biology,，2015，16(2)：67-76.

[4] BAGHAIE A,，Yu Zeyun.Structure tensor based image interpolation method[J].AEU Electronics and Communications,，2015，69(2)：515-522.

[5] 賈茜,，易本順,，肖進(jìn)勝.基于結(jié)構(gòu)成分雙向擴(kuò)散的圖像插值算法[J].電子與信息學(xué)報(bào)，2014,，36(11)：2541-2548.

[6] 樊博,，楊曉梅，胡學(xué)姝.基于壓縮感知的超分辨率圖像重建[J].計(jì)算機(jī)應(yīng)用,，2013,，33(2)：480-483.

[7] 首照宇，廖敏璐,，陳利霞.改進(jìn)的基于稀疏表示的圖像超分辨率重建算法[J].計(jì)算機(jī)應(yīng)用與軟件,，2014，31(4)：201-204.

[8] XUN Z J.A fixed-point method for a class of super-large scale nonlinear complementarities problems[J].Computers & Mathematics with Applications,，2014,，67(5)：999-1015.

[9] MAISELI B,，ALLY N，Gao Huijun.A noise-suppressing and edge-preserving multiframe super-resolution image reconstruction method[J].Signal Processing,，2015(34)：1-13.

[10] PRUN V E,，NIKOLAEV D P，BUZMAKOV A V,，et al.Effective regularized algebraic reconstruction technique for computed tomography[J].Crystallography Reports,，2013，58(7)：1063-1066.

[11] 張曉克,，許建剛.超分辨率圖像重建技術(shù)研究[J].科技創(chuàng)新與應(yīng)用,，2014，32(11)：68-69.

[12] 劉哲,，張永亮,，郝珉慧.一種快速的超分辨率圖像重構(gòu)算法[J].光電子.激光，2013,，24(2)：372-377.

[13] PENG H,，RAO R，DIANAT S.Multispectral image denoising with optimized vector bilateral filter[J].Image Process,，2014,，23(1)：264-273.

[14] KYUNGSHIN D，SHIKMOON Y.Super-resolution image reconstruction using wavelet based patch and discrete wavelet transform[J].Journal of Signal Processing Systems,，2015,，81(1)：71-81.

[15] SALGADO C，DOLUI S,，MICHAILOVICH V.Reconstruction of hardy data using a split Bergman optimization approach[J].Image Analysis and Recognition,，2013，50(1)：589-596.

[16] KUMAR B K S.Image fusion based on pixel significance using cross bilateral filter[J].Image and Video Processing,，2013,，5(9)：1193-1204.

[17] YIN W，OSHER S,，GOLDFARB D,，et al.Bregman iterative algorithms for L1-minimization with applications to compressed sensing[J].SIAM J Image Science,，2008,，1(1)：143-168.

[18] WUNDERLI T.Total variation time flow with quantile regression for image restoration[J].Mathematical Analysis and Applications，2013,，403(1)：272-282.

[19] ZHOU L,，LU X B，XUE T.A local structure adaptive super-resolution reconstruction method based on BTV regularization[J].Multimedia Tools and Applications,，2014,，71(3)：1879-1892.