張 媛，劉 峰

　?。暇┼]電大學(xué) 圖像處理與圖像通信江蘇省重點(diǎn)實(shí)驗(yàn)室,，江蘇 南京 210003）

　　摘  要： 采用改進(jìn)的層次分析法分析道路狀況的多種因素，得出了當(dāng)?shù)缆钒l(fā)生緊急事故時(shí),，符合時(shí)效性,、安全性,、經(jīng)濟(jì)性的路段權(quán)值。然后根據(jù)實(shí)時(shí)交通信息,，利用改進(jìn)的Dijkstra算法,，探索了路徑權(quán)重計(jì)算方法，建立了交通網(wǎng)絡(luò)的運(yùn)行時(shí)間的加權(quán)圖,，驗(yàn)證了本方法在實(shí)際交通網(wǎng)絡(luò)中的應(yīng)用,，證實(shí)了方法的有效性和可行性。

　　關(guān)鍵詞： 智能交通系統(tǒng),；最優(yōu)路徑,；層次分析法；Dijkstra算法

0 引言

　　隨著城鎮(zhèn)人口的增長(zhǎng)和可用物理空間的日益缺乏,，交通管理面臨的挑戰(zhàn)越來(lái)越嚴(yán)峻,，繼續(xù)擴(kuò)大道路網(wǎng)絡(luò)來(lái)解決日益增長(zhǎng)的交通需求已經(jīng)被視為一個(gè)不可持續(xù)的方案。本文利用智能交通的動(dòng)態(tài)路徑選擇思想,，為駕駛員提供實(shí)時(shí)最優(yōu)路徑,，避開(kāi)擁擠路段，或根據(jù)駕駛員需求提供最優(yōu)路徑,，實(shí)現(xiàn)智能且人性化的路徑誘導(dǎo),。在實(shí)際車輛行駛時(shí)，由A地到達(dá)B地的最佳路徑的標(biāo)準(zhǔn)不只是道路距離,、路面質(zhì)量,、交通擁堵、駕駛習(xí)慣等因素中的某單一標(biāo)準(zhǔn),，從駕駛員心理角度出發(fā),，依據(jù)每個(gè)人內(nèi)心的不同的標(biāo)準(zhǔn)，綜合考慮多種影響因素以后得出最能夠接受的方案,，從而獲得車輛行駛的最佳選擇,。

　　目前，有十多種計(jì)算最優(yōu)路徑的方法,，其中Dijkstra算法是理論上最完善的方法,，已被GIS系統(tǒng)廣泛采用。同時(shí)它也存在以下缺點(diǎn)：（1）它的計(jì)算僅僅基于道路的長(zhǎng)度,，而不考慮影響道路交通的實(shí)際因素,，如道路等級(jí)、道路上的交通擁堵等其他因素,，所以在復(fù)雜的交通環(huán)境中結(jié)果往往并非最優(yōu),。（2）在有大量節(jié)點(diǎn)的交通網(wǎng)絡(luò)中,，拓?fù)浣Y(jié)構(gòu)中占用大量的存儲(chǔ)空間,，且遍歷算法的搜索效率很低。

　　本文提出了層次分析法（Analytic Hierarchy Process，AHP）[1]的最優(yōu)路徑選擇模型,，運(yùn)用運(yùn)籌學(xué)中的AHP計(jì)算路徑的權(quán)重,，然后利用改進(jìn)的Dijkstra算法獲得最佳路徑。這種復(fù)雜的路徑?jīng)Q策算法可應(yīng)用于復(fù)雜路況的選路,，尤其適用于應(yīng)急救援,、多目標(biāo)決策的情況。

1 路段權(quán)重的判定

　　1.1 層次分析法介紹

　　層次分析法是一種解決復(fù)雜,、模糊問(wèn)題的簡(jiǎn)單決策方法,，特別是如本文討論的“最優(yōu)路徑”等難以進(jìn)行定量分析的問(wèn)題。現(xiàn)實(shí)情況是不僅道路的長(zhǎng)度不同,，受到交通狀況,、路面質(zhì)量、天氣條件等因素的影響,，各道路上的車輛行駛時(shí)間都會(huì)不同,。采用層次分析法，所有這些因素都被考慮,，通過(guò)各自不同的重要性影響路徑權(quán)重,。于是得到了一個(gè)更貼近現(xiàn)實(shí)的交通網(wǎng)絡(luò)有向圖加權(quán)圖。

　　通常,，該方法可分為三個(gè)步驟：

　?。?）建立層次結(jié)構(gòu)模型；

　?。?）構(gòu)造各層次的判斷矩陣,；

　　（3）實(shí)施層次排序和一致性檢驗(yàn),。

　　1.2 建立層次分析法模型

　　本文考慮了現(xiàn)實(shí)條件下可能影響駕駛員路徑選擇的因素,，除了一些常見(jiàn)的因素（如路徑距離，道路等級(jí),，車輛限制,，交通流量，氣候條件）[2-4]以外,，如果車輛前方路段突然發(fā)生車禍,、坍塌等嚴(yán)重事故，可能造成交通完全癱瘓,，嚴(yán)重影響車輛行駛的時(shí)間成本,，所以獲得的實(shí)時(shí)前方路況需要實(shí)時(shí)更新。此外在復(fù)雜道路情況下,，駕駛員對(duì)道路的熟悉程度也部分地影響了行駛時(shí)間,。所以設(shè)定集合：S={路徑距離/車速,，道路等級(jí)，交通流量,，車輛限制,，氣候條件，實(shí)時(shí)路況信息,，駕駛熟悉度},。根據(jù)層次分析法的思想，將層次結(jié)構(gòu)分為3層（如圖1所示）,，最上層為目標(biāo)層：路徑權(quán)重W,；中間層是準(zhǔn)則層，即集合S中的各項(xiàng)指標(biāo),；底層是方案層,，即計(jì)算所得的最優(yōu)路徑。

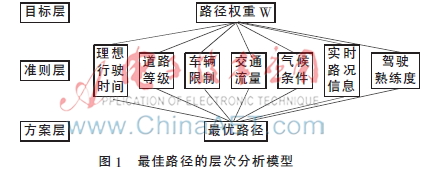
　　在使用AHP時(shí),，必須注意矩陣的一致性,。如果不滿足一致性，則結(jié)果錯(cuò)誤,。Jiang Hua[5]提出的AHM方法可以避免檢測(cè)一致性,，從而能確保決策不會(huì)出現(xiàn)：a>b，b>c,，得出c>a這種情況,。

　　1.3 計(jì)算基于實(shí)時(shí)交通信息的權(quán)重值

　　步驟1：利用層次分析法計(jì)算準(zhǔn)則層各指標(biāo)對(duì)于目標(biāo)層的權(quán)重w1、w2,、w3,、w4、w5,、w6,、w7。

　　對(duì)準(zhǔn)則層的各因素按1~9標(biāo)度思想分別賦值,，含義見(jiàn)表1[6],。

　　準(zhǔn)則層的各個(gè)準(zhǔn)則占最終結(jié)果的比重不一定相同，從駕駛員的需求出發(fā),，給它們?cè)O(shè)定不同的比例,。由此構(gòu)造出判斷矩陣，如表2所示,。

　　步驟2：計(jì)算權(quán)重的方法有幾何平均法,、算術(shù)平均法、特征向量法和最小二乘法,。本文選用特征向量法,，公式為：

　　AW=λmaxW（1）

　　λmax為判斷矩陣的最大特征值,，存在唯一的W的分量為正分量，將求得的W作歸一化處理即為特征向量,。

　　步驟3：上述方法計(jì)算的判斷矩陣通常是不一致的，為了獲得它對(duì)應(yīng)于最大特征值的特征向量,，被比較因素的權(quán)重向量不一致程度應(yīng)在容許的范圍內(nèi),，以保證其可靠性，所以必須進(jìn)行一致性檢驗(yàn)[7],。

　　一致性指標(biāo)：

　　CI=（λmax-n）/（n-1）（2）

　　其中,，n是A的階數(shù)。RI為平均隨機(jī)一致性指標(biāo),，取值參考表3,。

　　對(duì)判斷矩陣的一致性進(jìn)行檢驗(yàn)：

　　CR=CI/RI（3）

　　當(dāng)CR小于10%時(shí)，認(rèn)為判斷矩陣的一致性是令人滿意的,，否則應(yīng)當(dāng)進(jìn)一步修正判斷矩陣,。

　　步驟4：在獲得了各因素的權(quán)重值以后，計(jì)算路段權(quán)重,，并對(duì)路段權(quán)重進(jìn)行等值的無(wú)量綱處理[8],。

　　W=s/v（w2r+w3l+w4f+w5w+w6m+w7c）（4）

　　其中s是實(shí)際路段長(zhǎng)度，v是車輛平均行駛速度,，s/v則是理想情況下車輛勻速行駛所用的時(shí)間,；r是道路等級(jí)，根據(jù)公路的使用任務(wù),、功能和流量劃分為5個(gè)等級(jí)（0.2,、0.4、0.6,、0.8,、1.0）；l是交通流量,，與設(shè)計(jì)交通流量作比較,，比值由低到高賦以[0，1]區(qū)間內(nèi)的實(shí)數(shù),；f為車輛限制,，表示不同類型車輛的通行是否受限于該路段，受限則f=1,，否則f=0,；w是天氣狀況，根據(jù)車輛行駛的適宜程度賦以[0,，1]區(qū)間內(nèi)的實(shí)數(shù),；m是實(shí)時(shí)路況信息,，根據(jù)車輛獲得實(shí)時(shí)路況的能力賦以[0，1]區(qū)間的實(shí)數(shù),；c是駕駛員對(duì)路段的熟悉程度,，駕駛員通常主觀傾向于自己較熟悉的道路，賦以（0,，1）區(qū)間的實(shí)數(shù),，若取值在0附近，則選取的可能性較小,。

　　步驟5：實(shí)時(shí)更新交通信息,。

　　信息采集系統(tǒng)包括車輛信息采集設(shè)備和路邊信息采集設(shè)備，將采集的信息發(fā)送到信息監(jiān)控中心,。為了獲取各路徑交通信息,，更好地實(shí)現(xiàn)交通誘導(dǎo)，本文設(shè)計(jì)了一種基于socket通信[9]的模擬車輛運(yùn)行狀態(tài)采集方法,，將車輛作為客戶機(jī),，采集中心作為服務(wù)器，采用TCP/IP通信協(xié)議,。通信流程圖如圖2,。

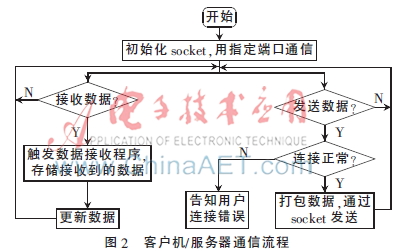
　　每一個(gè)客戶機(jī)代表一輛車，客戶機(jī)程序產(chǎn)生以下信息,，向服務(wù)器發(fā)送,，如表4。

　　服務(wù)器接收以上客戶機(jī)發(fā)送的數(shù)據(jù),，得出某一路段的實(shí)時(shí)道路信息,，若大量車聚集在某一個(gè)路段，則可判斷該路段的權(quán)重增大,。結(jié)合路邊信息采集設(shè)備獲得的數(shù)據(jù)和駕駛員自身判斷因素,，可以得到準(zhǔn)則層7個(gè)影響判決因素的模擬數(shù)值。

2 綜合最優(yōu)路徑算法

　　2.1 Dijkstra算法介紹

　　Dijkstra[10]算法是圖論中求解最短路徑的一個(gè)著名的算法,，用于求圖中一個(gè)節(jié)點(diǎn)到其他各個(gè)節(jié)點(diǎn)的最短路徑,。將道路抽象為圖論中的邊，交叉口抽象為節(jié)點(diǎn),。道路相關(guān)的參數(shù)影響邊的權(quán)值,，權(quán)值是廣泛的，可以表示速度,、天氣情況,、交通情況、距離等。衡量最短路徑的準(zhǔn)則是計(jì)算出的路徑權(quán)值W的大小,，并且邊的權(quán)值都是非負(fù)數(shù),。網(wǎng)絡(luò)中所有節(jié)點(diǎn)初始化為未標(biāo)記節(jié)點(diǎn)，在搜索過(guò)程中與最短路徑中的節(jié)點(diǎn)相連通的節(jié)點(diǎn)稱為臨時(shí)標(biāo)記節(jié)點(diǎn),，每次循環(huán)都從臨時(shí)標(biāo)記節(jié)點(diǎn)開(kāi)始搜索距源點(diǎn)最短的路徑長(zhǎng)度的節(jié)點(diǎn),，將其變?yōu)橛谰脴?biāo)記節(jié)點(diǎn)。直到所有節(jié)點(diǎn)都成為永久標(biāo)記節(jié)點(diǎn),，算法運(yùn)行結(jié)束,。

　　傳統(tǒng)的Dijkstra算法是從起點(diǎn)V到圖的剩余頂點(diǎn)的最短路徑的長(zhǎng)度增加的序列，它用于解決有向加權(quán)圖的問(wèn)題[11],。其基本思想是：首先建立一個(gè)節(jié)點(diǎn)集S,，選擇貪婪算法不斷擴(kuò)展集合S,。假設(shè)所有節(jié)點(diǎn)的集合是V,，S的初始值是源節(jié)點(diǎn)，T是存在于V中但不在S中的節(jié)點(diǎn)集,，T的初始值是除源節(jié)點(diǎn)外的所有節(jié)點(diǎn),。T中的節(jié)點(diǎn)根據(jù)路徑長(zhǎng)度的升序逐個(gè)進(jìn)入S，直到可以從源節(jié)點(diǎn)到達(dá)的節(jié)點(diǎn)全部進(jìn)入S,。然而,，把Dijkstra算法應(yīng)用到基于GIS的應(yīng)急救援體系，仍存在一定的不足：（1）該算法使用O（N2）的時(shí)間找到單源最短路徑,，使其低效地處理GIS系統(tǒng)中的海量數(shù)據(jù)[12],。（2）在路徑信息不變的情況下，搜索相同一對(duì)源點(diǎn)和目的節(jié)點(diǎn)時(shí),，得到的路線應(yīng)該是一樣的,。但此算法每次尋路都要重新計(jì)算最短路徑，浪費(fèi)時(shí)間,。（3）在傳統(tǒng)圖論網(wǎng)絡(luò)分析中,，每個(gè)路徑正反向權(quán)值是相同的。而實(shí)際交通中同一條道路兩個(gè)方向的路況可能差別非常大,，所以在仿真時(shí)采用不同的權(quán)重因子更加符合現(xiàn)實(shí)情況,。

　　2.2 對(duì)選路算法的改進(jìn)

　　本論文對(duì)此提出以下改進(jìn)：

　　（1）在GIS應(yīng)急救援系統(tǒng)中因?yàn)榻煌ňW(wǎng)絡(luò)特征的動(dòng)態(tài)變化特性,，一般順序計(jì)算產(chǎn)生的最短路徑樹不能完全滿足需要,。例如，當(dāng)汽車到達(dá)節(jié)點(diǎn)3,，發(fā)現(xiàn)道路L35交通堵塞非常嚴(yán)重時(shí),，必須重新尋路。這時(shí)，應(yīng)重新選擇3的鄰接結(jié)點(diǎn)來(lái)計(jì)算最短路徑樹T,。從動(dòng)態(tài)變化的特性出發(fā),，本文采用了逆向運(yùn)行的方法，即構(gòu)建一個(gè)逆向的最短路徑樹[13],，使源節(jié)點(diǎn)是終節(jié)點(diǎn),，且起始節(jié)點(diǎn)設(shè)在分支節(jié)點(diǎn)。此改進(jìn)適用于在行車至某一節(jié)點(diǎn)遇到前方路段突然發(fā)生車禍,、坍塌等嚴(yán)重事故,，造成交通完全癱瘓的情況。

　?。?）由于相同始末節(jié)點(diǎn)仍然會(huì)重新搜索,，造成資源浪費(fèi)，每次使用Dijkstra算法搜索完最優(yōu)路徑后,，將所有路段信息和最短路徑的信息加入到數(shù)據(jù)庫(kù)中,。用戶需要選擇路線時(shí)，程序先搜索數(shù)據(jù)庫(kù),，將之前保存的路線反饋出來(lái),。當(dāng)城市中道路狀況改變時(shí)，重新執(zhí)行Dijkstra算法,，更新數(shù)據(jù)庫(kù)中之前所有最短路徑信息[14],。

　　（3）在各指標(biāo)對(duì)于目標(biāo)層的權(quán)重系數(shù)中,，交通流量,、實(shí)時(shí)路況信息受到行駛方向影響較大，所以將這兩個(gè)因子根據(jù)路況靈活選取,，其他因子在同一條道路上數(shù)值相同,。正反兩個(gè)方向的計(jì)算結(jié)果可能完全不同。本文將一段路徑正反向的某些參數(shù)設(shè)為不同值,，這樣更符合實(shí)際交通狀況,。

3 最優(yōu)路徑選擇仿真實(shí)驗(yàn)

　　在研究各種路徑算法后，本文選擇在MATLAB平臺(tái)上,，實(shí)現(xiàn)利用AHP計(jì)算權(quán)重的改進(jìn)的Dijkstra算法作為最優(yōu)路徑算法,。

　　首先，根據(jù)表2的判斷矩陣A,，計(jì)算可得特征向量w和特征值k,。經(jīng)計(jì)算最大特征值為：k=7.339 2，對(duì)應(yīng)的歸一化特征向量為：

　　wT={0.4048,，0.1184,，0.1119，0.1592，0.1257,，0.0478,，0.0322}

　　通過(guò)MATLAB編程計(jì)算得到：

　　CI=0.056 5

　　CR=0.041 6

　　說(shuō)明此矩陣的一致性可以接受。

　　然后,，結(jié)合以下某地區(qū)的交通示意圖3,，譬如節(jié)點(diǎn)7到12的距離為15 km；設(shè)計(jì)平均時(shí)速為80 km/h,；道路等級(jí)為一級(jí),，r=0.4；實(shí)際交通流量l=0.6,；路段對(duì)車輛通行無(wú)限制,，f=0；該時(shí)段天氣良好,，能見(jiàn)度較高,，a=0.1；路段可以及時(shí)獲得前方的路況信息,，m=0.2,；司機(jī)較熟悉此路段,，c=0.85,。本題s／v以min作為單位。利用公式（4）,，計(jì)算得節(jié)點(diǎn)7到12的權(quán)值為16.3,，其余路徑的權(quán)值略。

　　本實(shí)驗(yàn)由于節(jié)點(diǎn)數(shù)量較多,，僅測(cè)試由節(jié)點(diǎn)9到節(jié)點(diǎn)12的路徑,，仿真結(jié)果如下：

　　起始點(diǎn)（9）到終止點(diǎn)（12）的路徑為：9→10→6→12

　　路徑權(quán)重：44.4

　　根據(jù)實(shí)時(shí)采集的交通信息，若大量車輛行駛在10→6路段,，則該路段極其擁堵,，此路段的交通流量l無(wú)限接近于1，計(jì)算路徑權(quán)重變?yōu)?6.5,，數(shù)值明顯增大,。

　　再測(cè)試一次選路結(jié)果：

　　起始點(diǎn)（9）到終止點(diǎn)（12）的路徑為：9→11→4→7→12

　　路徑權(quán)重：45

　　可以看出，新選擇的最優(yōu)路徑權(quán)重遠(yuǎn)小于56.5,，本算法是方便可行的,，并且同時(shí)可以得到任意起點(diǎn)i到終點(diǎn)j的最短路徑。

4 結(jié)論

　　對(duì)于最優(yōu)路徑算法的研究,，本文充分考慮了各因素對(duì)行駛速度的影響,，將層次分析法引入應(yīng)急救援系統(tǒng)，分析計(jì)算得出了各因子的相對(duì)重要度。據(jù)此提出了一種基于實(shí)時(shí)路況的路徑權(quán)重計(jì)算方法,，采用基于經(jīng)典Dijkstra算法進(jìn)行改進(jìn)的路徑搜索算法,，使計(jì)算值更符合現(xiàn)實(shí)，實(shí)現(xiàn)了系統(tǒng)的時(shí)效性,、安全性,、經(jīng)濟(jì)性。在本文中,，該算法模型在遇到緊急情況時(shí),，結(jié)合交通實(shí)況能做出最佳決策，具有很強(qiáng)的現(xiàn)實(shí)意義,。

參考文獻(xiàn)

　　[1] Yang Fujin,， Tan Wenan， Shen Weiming,， et al. A dynamic critical path computation algorithm for enterprise process cooperative scheduling[C]. Computer Supported Cooperative Work in Design （CSCWD）,， 2010 14th International Conference on. IEEE， 2010：606-610.

　　[2] Li Caixia,， ANAVATTI S G,， RAY T. Analytical hierarchy process using fuzzy inference technique for real-time route guidance system[J]. Intelligent Transportation Systems， IEEE Transactions on,， 2014,， 15（1）：84-93.

　　[3] Yang Shu， Li Chunhua. An enhanced routing method with Dijkstra algorithm and AHP analysis in GIS-based emergency plan[C]. Geoinformatics,， International Conference on,， 2010：1-6.

　　[4] Qi Guanghui， Huang Ronggang,， Zhe Zeng,， et al. An AHP based multi-factors weight method for route selection of oil and gas pipelines[J]. Science of Surveying and Mapping， 2013,， 38（5）：122-125.

　　[5] Zhou Binbin,， Chen Xuebo. Path selection algorithm based on AHP for small-world with three-weight[C]. Control and Decision Conference， Chinese.IEEE,， 2014：3627-3631.

　　[6] 張慧.基于層次分析法的應(yīng)急救援最優(yōu)路徑選擇分析[J].交通標(biāo)準(zhǔn)化,，2014（3）：68-71.

　　[7] Ma Wenjing， Xu Yingzhuo,， Xie Hui.The optimal path algorithm for emergency rescue for drilling accidents[C].Network Infrastructure and Digital Content,， 2009.IC-NIDC 2009.IEEE International Conference on. IEEE， 2009：866-870.

　　[8] 江文奇.無(wú)量綱化方法對(duì)屬性權(quán)重影響的敏感性和方案保序性[J].系統(tǒng)工程與電子技術(shù),，2012,，34（12）：2520-2523.

　　[9] Song Guoqing. The study and design of network traffic monitoring based on socket[C]. Computational and Information Sciences （ICCIS）,， 2012 Fourth International Conference on， 2012：845-848.

　　[10] YERSHOV D S,， LAVALLE S M. Simplicial Dijkstra and A*algorithms： from graphs to continuous spaces[J]. Advanced Robotics,， 2012， 26（17）：2065-2085.

　　[11] Yin Tieyuan,， Yang Jianyong. Dynamic application of the path selection in the road[C]. Proceedings of 2010 IEEE International Conference on Software Engineering and Service Sciences,， 2010.

　　[12] 李寬榮，陸通,，高勇.一種基于STL的高效最短路徑算法[J].科技創(chuàng)新導(dǎo)報(bào),，2014（12）：37-37.

　　[13] 任剛，王煒.轉(zhuǎn)向約束網(wǎng)絡(luò)中的對(duì)偶最短路徑樹原理及其原型算法[J].交通運(yùn)輸工程學(xué)報(bào),，2008,，8（4）：84-89.

　　[14] 劉帥修.智能交通中的路徑選擇及其移動(dòng)終端信息展示系統(tǒng)[D].南京：南京郵電大學(xué)，2012.