代曦，李騫,，顧大權(quán),，黃巖

　　(解放軍理工大學(xué) 氣象海洋學(xué)院，江蘇 南京 211101)

　　摘要：等值線編輯是對各形勢場等值線自動化分析結(jié)果的人工修正,，是對提取準(zhǔn)確等值線結(jié)果的必要補(bǔ)充,。針對已有等值線交互編輯方法難以滿足不相交約束、操作復(fù)雜等問題,，提出一種基于拉普拉斯坐標(biāo)系的等值線交互編輯方法,。實(shí)驗(yàn)結(jié)果表明，編輯結(jié)果有效保持了原有等值線的形狀拓?fù)?，且人工操作更少,，可滿足業(yè)務(wù)應(yīng)用中等值線交互編輯需求。

　　關(guān)鍵詞：等值線; 三角剖分,；拉普拉斯

0引言

　　*基金項(xiàng)目：國家自然科學(xué)基金項(xiàng)目資助（41305138,，41174164）等值線是將數(shù)據(jù)某一數(shù)量指標(biāo)值相等的各點(diǎn)連成的平滑曲線，它具有連續(xù)性,、不相交等特點(diǎn)?，F(xiàn)有等值線分析主要分為手工分析和軟件自動分析兩種，其中手工分析相對復(fù)雜,、耗時較長,，但此方法優(yōu)勢在于可融合預(yù)報人員經(jīng)驗(yàn)與其氣象要素信息；自動分析采用網(wǎng)格追蹤等方法對格點(diǎn)數(shù)據(jù)進(jìn)行跟蹤,，分析速度快,，但與手工分析結(jié)果存在一定差距，不能很好地滿足業(yè)務(wù)需求,。當(dāng)前大多數(shù)可視化及氣象分析軟件已實(shí)現(xiàn)等值線的自動分析功能,，SURFER、Micaps,、Grads、MATLAB,、ARCGIS,、Tecplot等均有等值線分析模塊［12］,。上述系統(tǒng)的主要問題表現(xiàn)在：訂正結(jié)果不能滿足等值線網(wǎng)格局部的拓?fù)浣Y(jié)構(gòu)需求；修正等值線時容易出現(xiàn)等值線相交的情況,；只能實(shí)現(xiàn)對單條等值線進(jìn)行修改,，如對多條線進(jìn)行修改，需要反復(fù)操作,，效率低,。

　　針對上述問題，本文提出了一種基于拓?fù)浣Y(jié)構(gòu)的等值線修正方法,。首先對已有的等值線數(shù)據(jù)進(jìn)行三角剖分,，依據(jù)剖分結(jié)果識別等值線間的拓?fù)潢P(guān)系，并對剖分結(jié)果建立Laplacian坐標(biāo)系［34］,。然后由用戶交互輸入修改意圖,，在交互修改過程中通過Laplacian坐標(biāo)對等值線修改移動部分進(jìn)行約束，同時通過笛卡爾坐標(biāo)約束固定點(diǎn),，通過最小二乘法求解移動點(diǎn)和固定點(diǎn)雙重約束下的線性系統(tǒng),，從而重新修改移動點(diǎn)［56］。通過上述方法,，可以實(shí)現(xiàn)在保持等值線集合拓?fù)浣Y(jié)構(gòu)的前提下對等值線進(jìn)行修改,。

　　本文提出方法的流程如圖1所示?！　?/p>

1三角剖分

　　三角剖分是計算機(jī)輔助幾何設(shè)計,、幾何造型及計算機(jī)圖形學(xué)中研究的重要內(nèi)容之一。本文將等值線集合進(jìn)行離散化并對得到的離散點(diǎn)進(jìn)行三角剖分得到三角網(wǎng)格,。目前,，三角剖分可以通過動態(tài)規(guī)劃［7］和德勞內(nèi)三角剖分算法［8］實(shí)現(xiàn)，但動態(tài)規(guī)劃算法主要是通過計算最短邊來排除病態(tài)的三角網(wǎng)格,。而在等值線族中,，由于等值線彎曲變化，部分等值線在某一個區(qū)域內(nèi)較為集中,，通過動態(tài)規(guī)劃算法來實(shí)現(xiàn)三角剖分可能丟失等值線間的拓?fù)潢P(guān)系,。因此，本文采用德勞內(nèi)三角剖分算法,。其主要流程如圖2所示,。

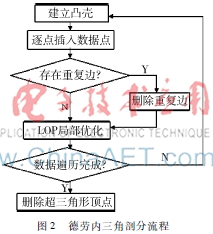
　　首先建立凸殼，包含了所有的離散點(diǎn),，然后向其中插入一點(diǎn),，該點(diǎn)與包含它的三角形三個頂點(diǎn)相連，形成三個新的三角形，然后逐個對它們進(jìn)行空外接圓檢測,，同時用Lawson設(shè)計的局部優(yōu)化過程LOP進(jìn)行優(yōu)化,，即通過交換對角線的方法來保證所形成的是Delaunay三角網(wǎng)。

2拓?fù)浣Y(jié)構(gòu)識別與Laplacian坐標(biāo)系建立

　　Laplacian坐標(biāo)表示方法又稱為微分坐標(biāo)方法或δ坐標(biāo)［9］,，或局部平均曲率法線,。在網(wǎng)格頂點(diǎn)處應(yīng)用Laplacian算子，可用于表征局部曲面的幾何特征,。建立拓?fù)浣Y(jié)構(gòu)后,，將笛卡爾坐標(biāo)系轉(zhuǎn)換為差分的拉普拉斯坐標(biāo)系。主要針對修改范圍內(nèi)的點(diǎn),，為下一步能量方程求解提供依據(jù),。

　　根據(jù)設(shè)定的修改范圍，從用戶選中的坐標(biāo)點(diǎn)出發(fā),，廣度搜索出一系列鄰接點(diǎn),，根據(jù)差分坐標(biāo)公式求出每點(diǎn)的δ坐標(biāo)。得到的坐標(biāo)存儲在鏈表中,。本文為了建立拉普拉斯坐標(biāo)系進(jìn)行如下定義：

　　(1)拉普拉斯網(wǎng)格

　　μ表示已知的N個點(diǎn)組成的三角網(wǎng)格,。V表示節(jié)點(diǎn)，E表示邊,，F(xiàn)表示平面,。每個i∈μ表示笛卡爾坐標(biāo)系中的節(jié)點(diǎn)用vi=(xi,yi,zi)表示。

　　首先通過中心和與它直接相連的節(jié)點(diǎn)定義差分坐標(biāo)系：

　　其中,，N(i)={j|(i,j)∈E},，表示與i節(jié)點(diǎn)相鄰節(jié)點(diǎn)的個數(shù)。

　　從絕對笛卡爾坐標(biāo)系到差分坐標(biāo)系的轉(zhuǎn)換可以表示為一個矩陣：

　　令D是一個對角陣,，Dii=di,，矩陣從絕對坐標(biāo)系轉(zhuǎn)換到關(guān)系坐標(biāo)系：

　　L=I－D－1A（4）

　　定義：

　　Ls=DL=D－A（5）

　　那么，

　　Lsx=Dδ(x),Lsy=Dδ(y),Lsz=Dδ(z)

　　其中x是n個向量包含x的絕對坐標(biāo)的所有頂點(diǎn),。

　　矩陣Ls被稱為拓?fù)淅绽咕W(wǎng)格,。圖形表示的拉普拉斯廣泛地應(yīng)用在代數(shù)和圖形學(xué)原理中，最主要的原因是因?yàn)樗拇鷶?shù)特性能很好地與圖形表示相結(jié)合,。從差分幾何角度來看,，δ坐標(biāo)系被視作離散化的連續(xù)拉普拉斯貝爾特拉米算子。

　　(2)三維仿射變換

　　常見的三維變換包括平移變換,、旋轉(zhuǎn)變換,、縮放變換、反射變換和錯切變換,。若取齊次坐標(biāo)來表示三維空間中的點(diǎn),，三維變換可表示為4×4的變換矩陣。

　　記(Tx,Ty,Tz)為平移向量， 繞x軸旋轉(zhuǎn)θ角的旋轉(zhuǎn)變換矩陣為：

　　同樣可以獲得繞y軸,、z軸旋轉(zhuǎn)的變換矩陣,。縮放矩陣為：

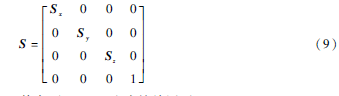
　　其中,，(Sx,Sy,Sz)為縮放因子。

3能量方程的求解

　　通過網(wǎng)格模型的笛卡爾坐標(biāo)構(gòu)造其Laplacian坐標(biāo),。由于變換矩陣L（或Ls）為奇異矩陣［10］,，不存在可逆矩陣，因此不能使用V′=L－1δ重建模型,。

　　由于Laplacian坐標(biāo)存在平移不變性,，因此變換矩陣L的秩為n-1。為了能夠唯一地重構(gòu)笛卡爾坐標(biāo)系中的網(wǎng)格模型,，需要求解一個滿秩的線性方程組,，因此需要指定更多的變形特征頂點(diǎn)的笛卡爾坐標(biāo)為約束條件。令空間中位置已知頂點(diǎn)的索引值集合為C,，有|C|個位置約束的形式為：

　　V′j=cj,j∈C

　　如果記C={1,2,...,m},，則需要求解的線性方程組表示如下：

　　方程組中的系統(tǒng)矩陣記為Lo。在本文中,，使用公式作為位置約束條件（或稱為模型約束條件）,。權(quán)值ω>0可以用來調(diào)整位置約束條件的重要性，每個約束都應(yīng)該有相應(yīng)的權(quán)值,，可以在Laplacian矩陣上針對不同行使用不同的權(quán)值,。附加的屬性約束條件使線性方程組成為超定方程組，因此基本上沒有完全精確的解,，可通過最小二乘法求解近似解,，當(dāng)系統(tǒng)滿秩時就存在唯一解：

　　式(11)的第一項(xiàng)表示盡可能保持原始網(wǎng)格的Laplacian坐標(biāo)不變，第二項(xiàng)表示盡可能減少特征頂點(diǎn)處的誤差,。求解值的精確度與現(xiàn)行方程組的約束條件有很大關(guān)系,。

　　基于線性邊約束的網(wǎng)格編輯方法在模型重建時，通過最小二乘系統(tǒng)求解獲得的模型為近似解,。當(dāng)模型集合細(xì)節(jié)特征較復(fù)雜時,，一次求解不一定能獲得較高質(zhì)量的變形效果，需要多次迭代求解,，逐漸逼近精確值,。

4實(shí)驗(yàn)結(jié)果與分析

　　為了驗(yàn)證方法的可行性，本文分別使用仿真數(shù)據(jù)和2011年數(shù)據(jù)庫中選取的4月20日12時的全球等壓線數(shù)據(jù)進(jìn)行了實(shí)驗(yàn),。仿真數(shù)據(jù)為16條平行線,，共510個采樣點(diǎn)。全球等值線數(shù)據(jù)共有682條等值線，19 985個采樣點(diǎn),。

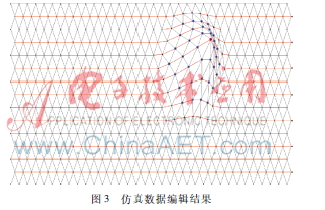
　　圖3仿真數(shù)據(jù)編輯結(jié)果通過上文提到的兩個過程,，用戶交互編輯修改點(diǎn)，使其帶動修改范圍內(nèi)的點(diǎn)一起移動,，從而達(dá)到修改的效果,，實(shí)驗(yàn)結(jié)果如圖3。其中用戶交互修改的點(diǎn)只有淺色的點(diǎn),，深色的點(diǎn)均根據(jù)淺色點(diǎn)移動而改變位置,，從而達(dá)到等值線修改范圍內(nèi)自動編輯的要求。

　　本文對全球數(shù)據(jù)的局部進(jìn)行編輯實(shí)驗(yàn),，根據(jù)修改范圍不同編輯結(jié)果如圖4,。圖4的修改范圍為2個網(wǎng)格。

　　從實(shí)驗(yàn)結(jié)果可以看出,，不同的修改范圍得到的數(shù)據(jù)編輯結(jié)果是不同的,。最后本文對全球數(shù)據(jù)進(jìn)行了編輯實(shí)驗(yàn)，如圖5所示,。其中用戶選擇的修改范圍在左下角,。

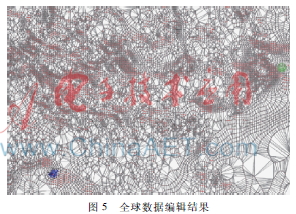
　　實(shí)驗(yàn)結(jié)果證明，采用本文方法對等值線數(shù)據(jù)進(jìn)行局部自動修正是可行性的,。

參考文獻(xiàn)

　?。?］ 王軟宏. 等值線的自動繪制方法及在計算機(jī)上的實(shí)現(xiàn)［D］.吉林：吉林大學(xué)數(shù)學(xué)研究所，2003.

　?。?］ 中國氣象局.MICAPS3.2 用戶使用手冊［Z］. 2012.

　?。?］ SORKINE O， LIPMAN Y,， COHENOR D,， et al. 2004.Laplacian surface editing［C］. In SGP′04: Proceedings of the 2004 Eurographics/ACM SIGGRAPH Symposium on Geometry Processing, ACM, New York, USA:175184.

　　［4］ LIPMAN Y, SORKINE O, COHENOR D, et al. Differential coordinates for interactive mesh editing［C］. In Proceedings of Shape Modeling International (2004), IEEE Computer Society Press：181190.

　?。?］ BOTSCH M, BOMMES D, KOBBELT L. Efficient linear system solvers for mesh processing［J］. IMAMathematics of Surfaces XI, Lecture Notes in Computer Science,2005,3604：6283.

　?。?］ FLOATER M S. Mean value coordinates［J］. Computer Aided Geometric Design, 2003,20(1):1927.

　　［7］ 劉晶, 張九龍, 李曄, 等. 基于圖像不變特征與三角剖分的水印算法［J］. 西安理工大學(xué)學(xué)報, 2009, 25(2): 227230.

　?。?］ 余杰, 呂品, 鄭昌文. Delaunay 三角網(wǎng)構(gòu)建方法比較研究［J］. 中國圖象圖形學(xué)報, 2010, 15(8): 11581167.

　?。?］ 許斌,李忠科,宋大虎.基于支持向量機(jī)的 Laplacian 網(wǎng)格曲面孔洞修補(bǔ)算法［J］.計算機(jī)工程與設(shè)計, 2014, 35(1): 237242.

　　［10］ 王勇.基于流形學(xué)習(xí)的分類與聚類方法及其應(yīng)用研究［D］.長沙：國防科學(xué)技術(shù)大學(xué), 2011.