摘  要： 提出了一種用Surfer軟件提供的可編程方法對散點數(shù)據(jù)進行網(wǎng)格化，再用矩形追蹤法追蹤等值線的新方法,。利用新方法繪制出的等值線既具有高精度性和實用性,，又具有可維護性，這也表明該方法是一個實用,、有效的等值線繪制方法,。
關(guān)鍵詞： Surfer；等值線,；離散數(shù)據(jù)網(wǎng)格化,；矩形追蹤

　等值線圖是在石油勘探開發(fā),、采礦、地質(zhì),、地球物理,、地球化學(xué)和氣象等工程和技術(shù)領(lǐng)域內(nèi)應(yīng)用極廣的一種圖形，是眾多領(lǐng)域成果表示的重要圖件之一,。在等值線繪制過程中,，首先要對散點數(shù)據(jù)進行網(wǎng)格化，而常用的數(shù)據(jù)網(wǎng)格化方法（如距離加權(quán)法,、方位法,、趨勢面法、加權(quán)最小二乘法,、疊加法）的精度和有效性都不高,；Kriging估值技術(shù)雖然比傳統(tǒng)的估值技術(shù)具有更高的先進性和有效性，但這種方法目前還沒有得到廣泛應(yīng)用,，許多細(xì)節(jié)問題還處于研究階段,。本文介紹利用Surfer軟件提供的可編程方法對散點數(shù)據(jù)進行網(wǎng)格化，然后用矩形追蹤法對網(wǎng)格化后的數(shù)據(jù)進行追蹤,，并實現(xiàn)了放大、縮小,、漫游,、光滑等功能，繪制出的等值線具有更強的實用性,。
1 繪制等值線圖原理
1.1 離散數(shù)據(jù)網(wǎng)格化
　為了繪制等值線圖,，首先需要把離散分布的數(shù)據(jù)點網(wǎng)格化。為此,，要建立數(shù)字高程模型（DEM）,，其主要功能就是將離散數(shù)據(jù)網(wǎng)格化。其主要步驟為：首先,，由原始數(shù)據(jù)點的橫,、縱坐標(biāo)的最小值和最大值構(gòu)成矩形網(wǎng)格的邊界；然后,，根據(jù)用戶需要將矩形再劃分為m×n個小矩形,，即形成矩形網(wǎng)格；最后,，用插值算法得到每個網(wǎng)格點的高程值,。
　DEM內(nèi)插有多種算法，常用的有距離加權(quán)法,、樣條函數(shù)內(nèi)插,、最小二乘配置法和Kriging方法等,。本文使用Suffer軟件中提供的可編程方法對散點數(shù)據(jù)網(wǎng)格化，其具體算法如下,。
?。?）輸入?yún)?shù)；
?。?）根據(jù)輸入?yún)?shù)從數(shù)據(jù)庫提取X,、Y坐標(biāo)及高程值Z，并保存到文本數(shù)據(jù)文件,；
?。?）在程序中引用surfer并創(chuàng)建surfer（srf）和grid（grd）對象；
?。?）用srf對象的GridData方法將文本文件轉(zhuǎn)換成surfer格式文件（.grd文件）,；
　（5）用grd對象的GetNode方法獲取grd文件里生成的網(wǎng)格點高程值,，寫入網(wǎng)格化后的數(shù)據(jù)文件,。
1.2 等值點的計算
　令任意一個網(wǎng)格邊兩端的數(shù)據(jù)值分別為Z1、Z2,，如圖1所示,，對于任意一條等值線W，它在該邊上Z（x,，y）-W=0,，即等值線所通過的點，可以有0~3個根,。

　當(dāng)?shù)戎稻€恰好等于網(wǎng)格節(jié)點的值時,，這種網(wǎng)格點被稱作退化點，當(dāng)遇到退化點時,，在網(wǎng)格點值上加上一個非常小的正數(shù),，以消除退化點[3]。
　如圖1中的Z1,、Z2值都不會等于等值線W的值,，這時，網(wǎng)格邊上對于某一條等值線W,，存在根Z（x,，y）-W=0的可能性有：
　（1）Z1>W,，Z2>W或Z1<W,，Z2<W時，沒有根,，如圖1中的（a）和（b）,，或存在兩個根,，如圖1的（e）和（f）。
?。?）Z1<W,，Z2>W或Z1>W，Z2<W時,，存在一個根,，如圖1中的（c），或存在兩個根,，如圖1中的（d）,，其中A根是重根，如圖1中的（g）,。
　對于立方函數(shù),，利用數(shù)值法求根。這時可以將網(wǎng)格邊長nx和ny再分成等間距的細(xì)分段,，如圖1中的（d）所示,，然后求出每個細(xì)分段兩端的函數(shù)值Zk和Zk+1。當(dāng)Zk或Zk+1等于等值線值W時,，同樣需要加上一個非常小的正數(shù),，以消除退化點。這樣,，當(dāng)（Zk-W）（Zk+1-W）<0時,，說明該細(xì)分段上存在一個根。該細(xì)分段的長度可以小到以機器步長來計算,，最小可以到描繪儀機器步長的2倍，這樣可以保證在曲面函數(shù)上追蹤所得到的等值線連續(xù)光滑而不會發(fā)生方向上的突變,。在找到根值的細(xì)分段上,，再以Zk和Zk+1作線性內(nèi)插求得所在根及等值點的位置。
　數(shù)值法找根時有時會失根,，尤其對于重根情況,，如圖1（d）中的A根，由于它兩端的Zk和Zk+1都小于W,，因此（Zk-W）（Zk+1-W）>0,，A根就會失去，但這對于繪制等值線并無多大妨礙,，至多漏繪一些極小的封閉等值線或等值線應(yīng)該封閉而不完全封閉,。
1.3 等值線的追蹤
　把網(wǎng)格縱邊和橫邊的細(xì)分段所組成的小網(wǎng)格稱為單元，它們的4個節(jié)點稱為單元節(jié)點,，以區(qū)別于原始的網(wǎng)格與網(wǎng)格節(jié)點,。這樣,，對于每一個單元在其單元節(jié)點上求出函數(shù)值后（若遇到有退化點時，同樣需要通過加一個很小的正數(shù)來處理）,，有圖2所示的8種連接等值線的可能（其中+號表示節(jié)點值大于等值線值,，-號表示節(jié)點值小于等值線值）。
?。?）單元節(jié)點上函數(shù)值同時大于或同時小于等值線值時,，該單元內(nèi)沒有等值線通過，如圖2（a）所示,。
?。?）單元節(jié)點上函數(shù)值大于和小于等值線時，單元邊上要么存在兩個根,，要么存在4個根,。存在兩個根時，兩根在對邊上,，如圖2（b）,、圖2（c）所示，兩根在鄰邊上,，如圖2（d）,、圖2（e）、圖2（g）,、圖2（h）所示,；存在4個根時，4個根分別在單元的4個邊上,。對于兩個根的情況,，只要找到根的位置就可以相連；對于4個根的情況,，則需規(guī)定底邊根與左邊根相連,，右邊根與上邊根相連或底邊根與右邊根相連，右邊根與上邊根相連,，如圖2（f）所示,，這樣就能保證等值線間不會出現(xiàn)相交現(xiàn)象[4]。

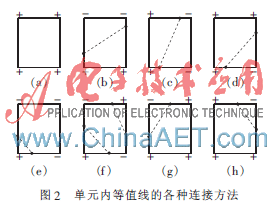
　圖3表示在一個矩形網(wǎng)格（i,，j）內(nèi),，將縱邊ny等分成6個細(xì)分段，將橫邊nx等分成5個細(xì)分段的連法示意圖,。在等分后的每個單元節(jié)點上算出函數(shù)值Z,。Z>W（W為等值線值）時，以“+”表示；Z<W時,，以“-”表示,。這樣在每個“+”、“-”節(jié)點之間必定存在一個等值線根,，可用線性內(nèi)插求出它的位置,，連成的等值線如圖3中的折線所示。由于網(wǎng)格邊上的函數(shù)是立方函數(shù),，它在網(wǎng)格邊上最多有3個根,，如圖3中，底邊上有3個根A1,、A2,、A3。在理論上只要對全部網(wǎng)格內(nèi)的單元節(jié)點掃描一遍,，把求得的根值用圖2中的規(guī)則相連即可畫出等值線圖,。

　但是這樣計算會花費計算機大量時間，而且大部分單元內(nèi)是不會有等值線通過的,。因此,，需要設(shè)計一種總等值線的方法，使得只在等值線會通過的單元節(jié)點上才求出函數(shù)值,，而大部分不通過等值線的單元不必求節(jié)點函數(shù)值,，以節(jié)省機器運算時間、加快速度,。這里還需指出,，圖3是一個復(fù)雜化的例子，實際上,，對于特定的等值線,，一個網(wǎng)格內(nèi)的等值線可能是很少的，或者只有一條或少數(shù)幾條,，還有很多網(wǎng)格根本就沒有,。此外，當(dāng)分段加密時,，等值線將逐漸變成光滑曲線，這是因為擬合網(wǎng)格點的函數(shù)是一個連續(xù)光滑的函數(shù),。因此,，利用上述方法，就不需要對等值線再作光滑處理,。
將等值線分為從邊界出發(fā)到邊界結(jié)束的等值線以及在內(nèi)部封閉的等值線兩種類型,，如圖4所示。無論哪種類型的等值線，都必須已知有順序相鄰的A1,、A2兩個等值點,。設(shè)它們的坐標(biāo)值分別為（a1x，a1y）及（a2x,，a2y）,，分別以nx和ny為單位長度，其坐標(biāo)的整數(shù)值為（a1j,，a1i）及（a2j,，a2i）。任意設(shè)兩個相鄰的單元如圖5中的單元Ⅰ,、Ⅱ所示,，A2落在單元Ⅰ和Ⅱ的鄰邊上，A1落在單元Ⅰ的其他三邊的任意一邊上,。用（i,，j）表示單元Ⅰ的序號，用（i+1,，j）,、（i，j+1）,、（i-1,，j）、（i,，j-1）表示單元Ⅱ的序號,，分別相當(dāng)于圖5中的（a）、（b）,、（c）,、（d）4種情況，則下一等值點追蹤方向依次由下述4個判別式確定,。

　
　 
　網(wǎng)格追蹤程序主要封裝在CContourTrace類中,。
　利用本文方法所生成的等值線如圖6所示。

　本文是提出了一種新的方法來實現(xiàn)等值線的繪制,，它首先用成熟軟件Surfer將原始數(shù)據(jù)進行網(wǎng)格化,，再利用矩形網(wǎng)格追蹤法追蹤網(wǎng)格，并按照實際需求實現(xiàn)了對等值線的縮放,、平移,、光滑和標(biāo)注等功能。利用本方法所繪制的等值線主要在石油勘探開發(fā),、采礦等領(lǐng)域得到應(yīng)用,。使用本方法所繪制的等值圖較其他方法效果更好、精確度更高、速度更快,，是一個實用有效的等值線繪制方法,。
參考文獻
[1] 王永會，宋曉宇,，欒方軍．基于網(wǎng)格的等值線圖快速生成算法[J]．計算機工程與應(yīng)用,，2001（17）：124-125.
[2] 陳學(xué)工，劉凱敏．一種基于格網(wǎng)法快速生成等值線的算法[J]．電腦與信息技術(shù),，2007,，15（3）：4-6.
[3] 宋麗娟，龔曉峰,，鐘猛．基于網(wǎng)格法的等值線繪制方法[J]．現(xiàn)代電子技術(shù),，2005，28（14）：65-67.
[4] 韋美雁,，杜丹蕾．基于規(guī)則網(wǎng)格的等值線的生成研究[J]．湖南科技學(xué)院學(xué)報,，2007，28（4）：39-41.
[5] 于嘉,，吳旭．一種改進的矩形網(wǎng)格等值線追蹤算法[J]．河南師范大學(xué)學(xué)報,，2008，36（6）：34-36.
[6] 張利,，王俊彪,，張賢杰．基于矩形網(wǎng)格追蹤法的曲面主曲率等值線生成算法[J]．計算機應(yīng)用研究，2009,，26（8）：3179-3181.