《電子技術(shù)應(yīng)用》
您所在的位置：首頁(yè) > 通信與網(wǎng)絡(luò) > 設(shè)計(jì)應(yīng)用 > 室外3D散射信道中ULA/UCA天線MIMO性能分析
室外3D散射信道中ULA/UCA天線MIMO性能分析
2016年電子技術(shù)應(yīng)用第7期
姚穎莉1,，周 杰1,，2,，王 益1,，劉 鵬1
1.南京信息工程大學(xué) 氣象探測(cè)與信息處理重點(diǎn)實(shí)驗(yàn)室,，江蘇 南京210044,； 2.日本國(guó)立新瀉大學(xué) 工學(xué)部電氣電子工學(xué)科,，日本 新瀉950-2181
摘要： 為更好地解決室外三維（3D）空間域的移動(dòng)通信問(wèn)題，提出了一種新型室外3D空間域散射信道統(tǒng)計(jì)模型,，主要研究MIMO多天線系統(tǒng)的接收性能,。在宏蜂窩小區(qū)移動(dòng)通信環(huán)境中，模型能夠估計(jì)多徑衰落信道的重要空間信道參數(shù),，首先推導(dǎo)了多徑衰落信道的到達(dá)角（Angle of Arrival,，AOA）概率密度分布。此外模型在設(shè)置多輸入多輸出（Multiple Input Multiple Output,，MIMO）多天線的均勻線性陣列（Uniform Linear Array,，ULA）和圓形陣列（Uniform Circular Array，UCA）的基礎(chǔ)上,，分析了波達(dá)信號(hào)不同方位角分布對(duì)散射信道中MIMO性能的影響因素,，包括MIMO空間相關(guān)性、信道容量以及天線陣列配置,。數(shù)值仿真結(jié)果與3D多徑衰落信道模型對(duì)比,，表明本模型的信道參數(shù)估計(jì)符合理論和實(shí)際的通信環(huán)境,，為評(píng)估MIMO天線接收系統(tǒng)與仿真無(wú)線通信系統(tǒng)提供了創(chuàng)新性的研究。
中圖分類號(hào)： TN911.6
文獻(xiàn)標(biāo)識(shí)碼： A
DOI：10.16157/j.issn.0258-7998.2016.07.022
中文引用格式： 姚穎莉,，周杰,，王益，等. 室外3D散射信道中ULA/UCA天線MIMO性能分析[J].電子技術(shù)應(yīng)用,，2016,，42(7)：87-90，94.
英文引用格式： Yao Yingli,，Zhou Jie,，Wang Yi，et al. An analysis of Doppler shift and MIMO performance in a brief 3-D geometric channel model[J].Application of Electronic Technique,，2016，42(7)：87-90,，94.
An analysis of Doppler shift and MIMO performance in a brief 3-D geometric channel model
Yao Yingli1,，Zhou Jie1，2,，Wang Yi1,，Liu Peng1
1.Jiangsu Key Lab. of Meteorological Observation and Information Processing， Nanjing University of Information Science and Technology,，Nanjing 210044,，China； 2.Dept.of Electronic and Electrical Engineering,，Niigata University,，Niigata 950-2181，Japan
Abstract： In multi-path environments, in order to solve the problem of mobile communication in the three-dimensional space, this paper presents a new statistical model of the 3D spatial domain, which mainly studies the performance of the MIMO multi antenna system. In macrocell mobile communication environment, the model is able to estimate the multipath fading channel of important space channel parameters, the multipath fading channel of AOA probability density distribution are derived. In addition, the channel MIMO performance influencing factors is analyzed, including MIMO spatial correlation, channel capacity and antenna array configuration. The results of numerical simulation are compared with 3D multipath fading channel model,，which shows that the channel parameters of the model estimated are in line with the theory and the actual communication environment,，and it provides innovative research to evaluate the MIMO antenna receiving system and simulation of wireless communication system.
Key words : geometrical-based channel model；multipath fading,；angle of arrival,；MIMO；capacity

0 引言

    目前,，MIMO已在固定寬帶無(wú)線接入和4G LTE(Long Term Evolution)中實(shí)現(xiàn),，MIMO無(wú)線通信技術(shù)可以顯著提高無(wú)線傳輸系統(tǒng)的性能?？紤]MIMO系統(tǒng)的整體特性,，要獲得更大的容量，應(yīng)盡可能減少兩陣元間的相關(guān)性,，并使得相關(guān)性矩陣的各元素值盡可能的小,。因此,，構(gòu)建能夠準(zhǔn)確而有效描述無(wú)線傳輸系統(tǒng)中多經(jīng)效應(yīng)的信道模型，是設(shè)計(jì)和評(píng)估MIMO系統(tǒng)接收性能,、分析信道空時(shí)特性的前提條件[1-5],。學(xué)者們相繼提出了不同的統(tǒng)計(jì)信道模型，并假設(shè)不同的散射體分布或空間幾何分布來(lái)對(duì)室內(nèi),、室外環(huán)境中的信道多徑效應(yīng)進(jìn)行仿真分析,。在文獻(xiàn)[6-11]中，只經(jīng)歷一次反射的散射模型應(yīng)用最為廣泛,，且?guī)缀跛械膸缀文Ｐ投及趫A模型（Circular Model,，CM）、橢圓模型（Elliptical Model,，EM）或3-D圓形/橢圓模型的分類范疇,。3D模型可以將基站（Base station，BS）以及移動(dòng)臺(tái)(Mobile station,，MS)端的波達(dá)信號(hào)細(xì)化為水平面以及垂直面的空間角域,，描述更精確。SYED J N和PATWARY M N[6]提出了一種基站處設(shè)置指向性天線且適用于宏小區(qū)的三維統(tǒng)計(jì)模型,。MOHAMMAD A和ALSEHAILI S[7]又提出了一種針對(duì)微小區(qū)的三維橢球模型,。近年，JANASWAMY R和BALTZIS K B[8-10]等人提出了一種新型的相似三維模型,。以上所有的三維模型都是散射體均勻分布的對(duì)稱型模型,，僅研究其統(tǒng)計(jì)模型的三維AOA、TOA空時(shí)參數(shù),，而對(duì)信道模型中的MIMO多天線接收系統(tǒng)特性仍缺乏深入的研究與對(duì)比分析,。

    為解決上述問(wèn)題，針對(duì)宏蜂窩小區(qū)移動(dòng)通信環(huán)境,，本文提出了一個(gè)基于三維空間域的統(tǒng)計(jì)信道模型,，基站BS端設(shè)置定向天線，且其發(fā)射信號(hào)來(lái)自三維空間,，輸入到MS端的所有信號(hào)僅分布在二維水平面上的圓模型中,。模型不僅推導(dǎo)了衰落信道鏈路的概率密度分布，還基于這些分析更深入地研究散射信道中的ULA/UCA MIMO天線陣列系統(tǒng)性能,，為三維空間域的信道建模及MIMO接收系統(tǒng)的性能分析提供了有利的研究工具,。

1 3D散射信道模型 

    本文提出了一個(gè)簡(jiǎn)潔而且適應(yīng)于宏蜂窩無(wú)線通信環(huán)境的3D散射簇統(tǒng)計(jì)信道模型，如圖1所示,。其中MS與BS間的水平距離為D,，MS周圍的散射體均勻分布且被限制在一個(gè)圓形區(qū)域R內(nèi)，BS處使用主瓣寬度為2α的定向天線,，且與MS的水平高度差為h,。圖中僅標(biāo)注一個(gè)散射體,，但實(shí)際認(rèn)為有許多散射體分布于CM內(nèi)部。指向性天線分割散射體區(qū)域,，可能會(huì)使散射區(qū)域形成非對(duì)稱的信道模型,，如圖2所示。本文中,，MS配置單天線的ULA或UCA陣列,，如圖3所示。為簡(jiǎn)化研究與分析,，本文設(shè)定以下條件：文中的每個(gè)散射體均為全方位反射,，且獨(dú)立于其他散射體，并只經(jīng)歷一次反射,；MS遠(yuǎn)離散射區(qū)域的邊界,，且忽略相鄰小區(qū)的干擾；MS與BS間的每條傳輸路徑只與一個(gè)散射體有關(guān),。為推導(dǎo)MS端多普勒譜和MIMO天線系統(tǒng)的接收性能,，BS端設(shè)置主瓣寬度為2?琢的指向性天線，本文不考慮所有的天線極化影響[11],。

tx1-t1.gif

tx1-t2.gif

tx1-t3.gif

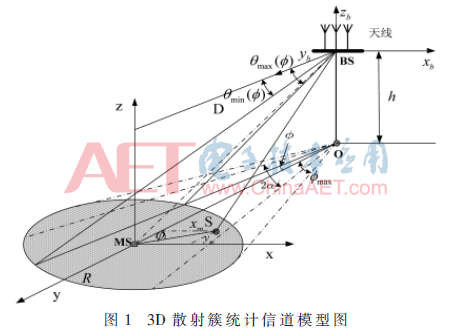
    如圖1所示，本文提出的信道模型可由半球體模型衰減得到,。模型的所有散射體僅分布在水平面內(nèi)的圓模型中,，這表示雖然BS的發(fā)射信號(hào)來(lái)自一個(gè)三維空間中，但所有輸入到MS端的信號(hào)最終都分布在水平面上的圓模型內(nèi),。當(dāng)BS處使用全指向式天線時(shí),，仰角平面內(nèi)的邊緣PDFs f(βm)=0，方位角平面內(nèi)的邊緣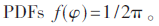tx1-t2-x1.gif當(dāng)BS處使用指向性天線時(shí),，MS處多徑分量的AOA特性不同于文獻(xiàn)[3-4]中的通用CM圓模型,。從圖1中可以發(fā)現(xiàn)，當(dāng)BS處使用主瓣寬度為2α的單位增益定向天線時(shí),，MS處多徑分量AOA的概率密度函數(shù)一定不會(huì)是常數(shù),。tx1-t2-x2.gif作為中間量，是圖中定向天線形成的所有散射圓盤(pán)覆蓋區(qū)域分割而成的一個(gè)個(gè)非天線覆蓋區(qū)域的面積,。指向性天線形成的所有散射圓盤(pán)覆蓋區(qū)域的面積計(jì)算式為：

tx1-gs1-4.gif

tx1-gs5.gif

2 ULA/UCA多天線MIMO分析

    本文中,，MS配置單天線的ULA或UCA陣列如圖3所示。從圖中可以直觀地發(fā)現(xiàn),，線性陣列結(jié)構(gòu)簡(jiǎn)單,，圓形陣列具有全方向性特性，在移動(dòng)通信領(lǐng)域應(yīng)用的較多,。本節(jié)將分析ULA/UCA陣列對(duì)MIMO天線系統(tǒng)空間衰落相關(guān)性,、信道容量等性能的影響,。

2.1 天線陣元間的空間衰落相關(guān)性

    MS端MIMO天線陣列為ULA時(shí)，入射信號(hào)的空間導(dǎo)向矢量為：

tx1-gs6-8.gif

    若假設(shè)波達(dá)信號(hào)水平方位角AOA遵循高斯分布,，則相應(yīng)的函數(shù)表達(dá)式為：

    tx1-gs9.gif

其中σG是功率譜分布標(biāo)準(zhǔn)差,。將式(6)、式(7),、式(9)代入式(8)中即可得到入射信號(hào)高斯分布時(shí)兩陣元間的空間相關(guān)性表達(dá)式,。

2.2 ULA/UCA多天線MIMO信道容量

    在無(wú)線通信系統(tǒng)性能分析中，信道容量能夠全面表征MIMO多天線系統(tǒng)的接收性能[12],。本小節(jié)將利用不同天線陣列的MIMO特性分析ULA,、UCA陣列對(duì)MIMO信道容量的影響。一般情況下會(huì)通過(guò)互補(bǔ)累積分布函數(shù)與各態(tài)歷經(jīng)容量描述隨機(jī)MIMO信道容量的統(tǒng)計(jì)特性,。當(dāng)系統(tǒng)的發(fā)送端無(wú)法獲知信道的傳輸信息時(shí),，最好的方法是將功率平均分配到各個(gè)天線的陣元上，此時(shí)一個(gè)突發(fā)時(shí)間內(nèi)信道容量的平均值為：

tx1-gs10.gif

3 數(shù)值結(jié)果與分析

    針對(duì)本文研究的室外三維空間域統(tǒng)計(jì)信道模型,，本節(jié)將通過(guò)數(shù)值計(jì)算和仿真給出波達(dá)信號(hào)不同角能量分布等因素對(duì)MIMO天線系統(tǒng)接收性能等的影響情況,。

圖4描述的是ULA/UCA在陣元1、2間,，波達(dá)信號(hào)水平方位角遵循本模型推導(dǎo)的信號(hào)分布以及高斯分布情況下的空間相關(guān)性,。從圖中可以看出，上述兩陣列在陣元間隔d,、r為零時(shí),，其空間相關(guān)性最大；d,、r從0增加到0.4λ,，陣元間空間相關(guān)性迅速下降；當(dāng)d>0.4λ,，r>0.4λ時(shí),，空間相關(guān)性緩慢減小，并趨于極限值,。兩陣列的空間相關(guān)性均隨著d/λ,、r/λ的增大而相對(duì)減小，但在下降速率上有差別,。從圖4(a),、圖4(b)的對(duì)比中可以發(fā)現(xiàn)，圖(a)分布情況下的ULA陣列空間相關(guān)性震蕩幅度較大,；且圖(a)所描述的空間相關(guān)性存在過(guò)零點(diǎn),，第一個(gè)過(guò)零點(diǎn)出現(xiàn)在d≈0.8λ的地方。此外，對(duì)比UCA陣列下的圖4(c),、圖4(d)可以發(fā)現(xiàn),， UCA陣列的空間相關(guān)性呈緩慢遞減趨勢(shì)，基本無(wú)大幅度的震蕩發(fā)生,，且無(wú)過(guò)零點(diǎn),。

tx1-t4.gif

    圖5描述的是與圖4對(duì)應(yīng)情況下的信道容量分布。從圖中可以發(fā)現(xiàn),，ULA,、UCA兩陣列的信道容量隨著d/?姿、r/?姿的增加呈遞增趨勢(shì),，且UCA陣列信道容量的震蕩幅度較大,。從圖中還可以發(fā)現(xiàn)，在ULA陣列的陣元間距d,、UCA陣列的圓環(huán)半徑r較?。ń咏?）時(shí)，由于陣元間的相關(guān)性較大（見(jiàn)圖4）,，使得信道容量較?。划?dāng)d,、r在(0,，0.4λ)范圍內(nèi)增加時(shí)，陣元間的相關(guān)性快速下降,，使得陣列的信道容量相應(yīng)地快速增加,；當(dāng)d與r大于0.4λ后，天線陣列的信道容量以小幅震蕩平穩(wěn)增長(zhǎng)到飽和,，最終趨于極限值,。比較ULA陣列下的圖5(a),、圖5(b)可以發(fā)現(xiàn),，圖5(b)曲線描述的信道容量增速較慢；比較UCA陣列下的圖5(c),、5(d)可以發(fā)現(xiàn),，在r∈(0，0.4λ)時(shí),，圖5(c)信號(hào)分布下的信道容量增長(zhǎng)更快,，且較先趨于極限值。 

tx1-t5.gif

4 結(jié)論

    本文提出了一種簡(jiǎn)易的三維空間域統(tǒng)計(jì)信道模型,，主要研究室外3D散射信道中ULA/UCA MIMO性能,。模型推導(dǎo)了多徑衰落信道的AOA概率密度函數(shù)，研究了ULA/UCA天線陣列、波達(dá)信號(hào)不同方位角分布對(duì)MIMO性能的影響等,。數(shù)值仿真結(jié)果與文獻(xiàn)[3,，7]等對(duì)比分析表明了該模型的信道參數(shù)估計(jì)的合理性，傳輸信號(hào)的性能更加優(yōu)越,，為分析MIMO系統(tǒng)的空間參數(shù)以及信道容量提供了更為靈活的理論支撐,。

參考文獻(xiàn)

[1] DAMNJANOVIC A，MONTOJO J,，WEI Y,，et al.A survey on 3GPP heterogeneous  networks：wireless communications[J].IEEE Wireless Communications，2011,，18(3)：10-21.

[2] ERTEL R B,，REED J H.Angle and time of arrival statistics for circular and elliptical scattering model[J].IEEE J.Sel.Areas Commun.，1999,，17(11)：1829-1840.

[3] PETRUS P,，REED J H，RAPPAPORT T S.Geometrical-based statistical macrocell channel model for mobile environment[J].IEEE Trans. Commun.,，2002,，50(3)：495-502.

[4] JIANG L，TANS Y.Simple geometrical-based AOA model for mobile communication systems[J].Electron Lett.,，2004,，40(19)：1203-1205.

[5] JIANG L，TAN S Y.Geometrically based power azimuth spectrum models for mobile communication systems[J].Microwave and Optical Technology Letters,，2007,，49(9)：2093-2097.

[6] SYED J N，PATWARY M N.3-D Gaussian density propagation model employing a directional antenna at BS[J].IEEE Trans.Veh.Technol.,，2010,，59(7)：3193-3204.

[7] MOHAMMAD A，ALSEHAILI S.Generalized three dimensional geometrical scattering channel model for indoor and outdoor propagation environments[C].PHD Dissertation,，Department of Electrical and Computer Engineering,，University of Manitoba，Canada,，2010,，109：191-209.

[8] JANASWAMY R.On random time and on the relation between wave and telegraph equations[J].IEEE Transactions on Antennas & Propagation，2013,，61(61)：2735-2744.

[9] BALTAIS K B,，SAHALOS J N.A simple 3D geometric channel model for macrocell mobile communication[J].Wireless Pers.Commun.，2009,，51(2)：329-347.

[10] HAO J,，JIE Z，KIKUCHI H.Angle and time of arrival statistics for a 3-D pie-cellular-cut scattering channel model[J].Wireless Personal Communications，2014,，78(2)：851-865.

[11] HUA M C,，LIU H C.Angle-of-arrival estimation of multipath signals in a passive coherent location system using OFDM-based illuminators[J].Wireless Personal Communications，2013,，77(2)：1-18.

[12] ZHOU J,，QIU L.Analyses and comparisons of geometrical-based channel model arisen  from scatterers on a hollow-disc for outdoor and indoor wireless environments[J].IET Communications，2012,，6(17)：2775-2786.

此內(nèi)容為AET網(wǎng)站原創(chuàng),，未經(jīng)授權(quán)禁止轉(zhuǎn)載。