張志禹,趙良辰,滿蔚仕
(西安理工大學(xué), 陜西 西安 710048)
摘要:S變換因其優(yōu)良的時(shí)頻特性而在故障定位方面獲得了廣泛的應(yīng)用,但由于S變換計(jì)算時(shí)采用等間隔采樣頻率點(diǎn),因而計(jì)算量較大,且存在運(yùn)算速度和測距精度之間的矛盾,即為了提高測距精度必須提高采樣頻率,但提高采樣頻率就會降低算法的運(yùn)算速度,降低了實(shí)時(shí)性。為此文章提出了一種自適應(yīng)于測距信號的S變換,該算法針對信號的特定成分進(jìn)行時(shí)頻分析,在提高測距精度的基礎(chǔ)上,減少了算法運(yùn)算量,保證了系統(tǒng)的實(shí)時(shí)性。并對包含噪聲情況下該方法的準(zhǔn)確度進(jìn)行了分析驗(yàn)證。實(shí)驗(yàn)結(jié)果證明,自適應(yīng)S變換在保證系統(tǒng)實(shí)時(shí)性的前提下能夠有效提高測距精度。
關(guān)鍵詞:行波測距;自適應(yīng);采樣頻率;精度
中圖分類號:TM 771文獻(xiàn)標(biāo)識碼:ADOI: 10.19358/j.issn.16747720.2016.23.002
引用格式:張志禹,趙良辰,滿蔚仕. 自適應(yīng)S變換在故障測距的應(yīng)用研究[J].微型機(jī)與應(yīng)用,2016,35(23):9-11,14.
0引言
我國配電網(wǎng)中普遍采用小電流接地系統(tǒng)[1],單相接地故障發(fā)生后,由于小電流系統(tǒng)不構(gòu)成短路回路,系統(tǒng)可在故障發(fā)生后繼續(xù)運(yùn)行1~2 h。因此,采用小電流接地方式對供電可靠性有顯著作用。但在故障狀態(tài)下長時(shí)間運(yùn)行,出現(xiàn)的過電壓(特別是弧光過電壓),可能引起絕緣的薄弱環(huán)節(jié)被擊穿,發(fā)展成為相間短路,使事故擴(kuò)大,影響用戶的正常用電。還可能使電壓互感器鐵心嚴(yán)重飽和,導(dǎo)致電壓互感器嚴(yán)重過負(fù)荷而燒毀,威脅電網(wǎng)的安全運(yùn)行[2]。因此,如何能夠快速準(zhǔn)確地定位單相接地故障發(fā)生位置,對于電力系統(tǒng)的穩(wěn)定運(yùn)行具有重要意義。
由于S變換優(yōu)良的時(shí)頻特性,利用S變換的行波測距法已經(jīng)成為故障定位的主要方法。而利用S變換的故障定位,通常是利用S變換的模時(shí)頻矩陣其中的某一頻率下的幅值時(shí)間曲線,實(shí)際上其余頻率點(diǎn)并未使用。由于S變換對所有頻率點(diǎn)都要進(jìn)行運(yùn)算,當(dāng)信號采樣頻率提高時(shí),采樣點(diǎn)數(shù)增加,S變換時(shí)間也大大增加,影響了故障測距的實(shí)時(shí)性。故本文提出了自適應(yīng)S變換,只計(jì)算故障信號特定頻率點(diǎn)下的S變換結(jié)果,大大減少了需要處理的數(shù)據(jù)量,節(jié)約了運(yùn)算時(shí)間。
1采樣頻率對誤差的影響
由D型行波測距法故障距離計(jì)算公式dmf=12(L+(tm-tn)v)可知,D型行波測距法誤差為:

式中,L為線路總長度,fs為采樣頻率,d為實(shí)際故障距離,v為行波波速。
由上式可以得到D型行波測距法測距精度為v/2f。當(dāng)采樣頻率為100 kHz時(shí),設(shè)波速近似為光速3×108 m/s,測距精度為1.5 km。實(shí)際工程中,1.5 km的測距精度能夠較好地滿足遠(yuǎn)距離輸電線路的故障測距需求,但對于短距離配電線路,則要求更高的測距精度。當(dāng)采樣頻率提高時(shí),測距精度也將提高,但同樣的,S變換的計(jì)算量也將大幅度提高。對于低壓配電線路,采樣頻率宜在10~20 MHz之間[3]。
當(dāng)采樣頻率為100 kHz時(shí),仿真時(shí)間設(shè)置為0.1 s,即采樣點(diǎn)數(shù)為10 000個(gè)時(shí),S變換計(jì)算的頻率點(diǎn)為5 000個(gè);而當(dāng)采樣頻率提高到10 MHz時(shí),采樣點(diǎn)數(shù)為1.0×106個(gè),所需計(jì)算的頻率點(diǎn)數(shù)為5.0×105個(gè),需要計(jì)算的數(shù)據(jù)量甚至已經(jīng)超出了MATLAB的存儲空間大小,計(jì)算時(shí)間過久,無法滿足實(shí)時(shí)處理的需求。
因此,本文提出采用自適應(yīng)S變換,簡化運(yùn)算過程,在提高測距精度的基礎(chǔ)上,保證算法實(shí)時(shí)性。
2自適應(yīng)S變換
2.1S變換基本原理
信號的S變換定義[4-7]如下:
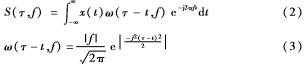
式中,ω(τ-t,f)為高斯窗口,f為頻率,τ為控制高斯窗口關(guān)于時(shí)間軸t的位置參數(shù)。由式(2)可以看出,不同于短時(shí)傅氏變換,S 變換的高斯窗口寬度及高度隨頻率變化而變化,從而克服了短時(shí)傅氏變換窗口寬度、高度固定不變的缺陷。
通過S逆變換,可以由S(τ,f)很好地重構(gòu)x(t),其逆變換公式如下:
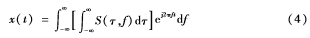
設(shè)信號x(kT),k=0,1,2,…,N-1是對連續(xù)時(shí)間信號x(t)采樣得來的離散時(shí)間序列,T是采樣間隔,N是采樣點(diǎn)數(shù)。該序列的離散傅里葉變換為:

2.2自適應(yīng)S變換原理
自適應(yīng)S變換實(shí)際上是利用預(yù)先確定好的信號中的有效頻率成分作為S變換的輸入,代替了S變換原本遍歷性的頻域迭代計(jì)算方式。對于應(yīng)用了S變換的行波測距法來說,通常是首先從S變換模時(shí)頻矩陣中提取特征向量,然后再利用這些參數(shù)進(jìn)行波頭識別以及故障定位。其中所提取的特征向量一般是S模時(shí)頻矩陣特定頻率下的時(shí)間幅值分量。因此如果能只針對特定頻率點(diǎn)進(jìn)行S變換,就可以大大減少工作量。其離散形式[8-9]的表達(dá)式為:
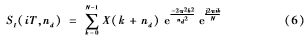
式中,nd為用來識別行波波頭的時(shí)間幅值分量所處的頻率點(diǎn)。其確定的主要依據(jù)是S變換后能清楚識別故障行波波頭,使其不被噪聲淹沒。自適應(yīng)S變換計(jì)算流程如下:
(1)利用FFT計(jì)算故障行波信號的離散傅里葉變換X(k);
(2)確定X(k)的頻率點(diǎn)nd;
(3)計(jì)算對應(yīng)于頻率點(diǎn)nd的高斯窗函數(shù)G(nd,k);
(4)將X(k)移位至X(k+nd),對X(k+nd)進(jìn)行加窗處理,也就是將X(k+nd)、G(nd,k)相乘,得到X(nd,k);
(5)求B(nd,k)反傅里葉變換,得到對應(yīng)于頻率點(diǎn)nd的S變換結(jié)果。
由于頻率點(diǎn)的選擇方法,當(dāng)噪聲大小以及故障點(diǎn)過渡電阻等條件發(fā)生改變時(shí),可能無法得到可以清楚識別波頭的時(shí)間幅值曲線。因此本文提出一種采用自適應(yīng)的辦法解決該問題,確定自適應(yīng)S變換頻率點(diǎn)。
主要原理是一個(gè)循環(huán)過程。實(shí)驗(yàn)發(fā)現(xiàn),相差1 kHz以下的頻率點(diǎn),分別進(jìn)行行波測距,所得到的測距結(jié)果幾乎相同。因此本文以最高頻率的40%頻率點(diǎn)為基準(zhǔn),以1 kHz為步長,當(dāng)所選的頻率點(diǎn)S變換結(jié)果,行波波頭被噪聲淹沒而無法識別波頭時(shí),降低所選頻率,再次進(jìn)行S變換,直至可以識別出行波波頭為止;當(dāng)S變換結(jié)果能夠識別波頭時(shí),判定波頭幅值是否高于噪聲平均幅值的50%。當(dāng)波頭幅值高于噪聲平均幅值50%時(shí),可以認(rèn)為波頭能夠被清楚地識別,如果不高于,則應(yīng)提高頻率,直至能夠清楚地識別行波波頭。該算法經(jīng)過3~4個(gè)頻率點(diǎn)的S變換即可得到最優(yōu)的頻率點(diǎn),與傳統(tǒng)S變換需要在106個(gè)頻率點(diǎn)處進(jìn)行S變換相比,計(jì)算量大大減少。
該方法流程圖如圖1。

3自適應(yīng)S變換的模型仿真驗(yàn)證
模型參數(shù)為:線路電壓等級為110 kV,頻率50 Hz。采樣頻率為10 MHz,仿真時(shí)長為0.1 s。線路全長132 km,故障點(diǎn)距離N端25 km。
線路結(jié)構(gòu)參數(shù)為:

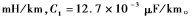
將實(shí)際線路參數(shù)代入波速計(jì)算公式 可以計(jì)算得到波速約為2.981 13×105 km/s。
可以計(jì)算得到波速約為2.981 13×105 km/s。
故障于0.035 s發(fā)生,M端監(jiān)測點(diǎn)測得的三相電壓如圖2所示,可以看出故障發(fā)生后,故障相相電壓明顯降低。

經(jīng)Clarke變換后,得到的α模分量如圖3。

由圖3可以看出,波形共包括1 000 000個(gè)采樣點(diǎn),如進(jìn)行完全S變換,則需在500 000個(gè)頻率點(diǎn)處進(jìn)行S變換,計(jì)算量巨大,運(yùn)算時(shí)間過長。由于高斯白噪聲的存在,如果選取過高頻率分量進(jìn)行行波測距將導(dǎo)致信噪比過低,噪聲影響加劇,無法識別行波波頭;如果頻率分量選取過低,則由于S變換窗函數(shù)寬度較寬,無法準(zhǔn)確地獲得初始行波波頭達(dá)到時(shí)刻,導(dǎo)致最終測距結(jié)果誤差變大,準(zhǔn)確率下降。因此,在S變換結(jié)果最高頻率為5 MHz的情況下,選取自適應(yīng)S變換的頻率點(diǎn)為2 MHz。得到的S變換結(jié)果如圖4。

由圖4可以看出,選擇初始頻率點(diǎn)即可準(zhǔn)確定位故障點(diǎn),波頭到達(dá)的時(shí)刻分別為352 854、350 841。根據(jù)雙端行波測距公式,取行波波速為計(jì)算波速2.981 13×105 km/s,最終測距結(jié)果為24.995 km,誤差5 m。
但當(dāng)系統(tǒng)所含噪聲增大時(shí),選擇初始頻率點(diǎn)未必就能準(zhǔn)確定位故障位置。圖5為系統(tǒng)噪聲為70 dBW時(shí),S變換結(jié)果中2 MHz頻率分量。

其中,M端觀測到的最大值為2 817,出現(xiàn)在721 762時(shí)刻處。此時(shí)M端無法觀測到明顯的波頭,最大值均未高出噪聲平均幅值50%。
因此,以1 kHz為步長,減小所選頻率。當(dāng)選擇頻率為1.5 MHz時(shí),所得分量如圖6。

M、N兩端,均可觀測到明顯的波頭,所得波頭到達(dá)時(shí)刻分別為352 853、350 841。根據(jù)雙端行波測距公式,取行波波速為計(jì)算波速2.981 13×105 km/s,得到最終的測距結(jié)果為25.01 km,誤差為10 m。
下面將自適應(yīng)S變換和S變換在不同區(qū)段上的故障
測距結(jié)果進(jìn)行比較。故障類型為A相接地故障,過渡電阻20 Ω,線路中包含60 dBW的噪聲。其中,自適應(yīng)S變換采樣頻率為10 MHz,S變換采樣頻率為100 kHz。測距結(jié)果如表1、表2所示。


可以看出,采用了自適應(yīng)S變換的故障測距算法,在保證系統(tǒng)實(shí)時(shí)性的基礎(chǔ)上,可以通過提高采樣頻率,減少測距誤差,在準(zhǔn)確度與實(shí)時(shí)性上較傳統(tǒng)S變換算法都具有很大優(yōu)勢。
4結(jié)論
本文在S變換的基礎(chǔ)上,提出了將自適應(yīng)S變換與故障定位結(jié)合的新方法,能夠大大減少所需的存儲空間以及計(jì)算量,大幅度提高采樣頻率,提高了定位的準(zhǔn)確度,同時(shí)對含噪情況下該方法的可靠性加以驗(yàn)證。盡管仿真結(jié)果比較令人滿意,但應(yīng)當(dāng)注意的是實(shí)驗(yàn)只是在理論基礎(chǔ)以及理想的模型上進(jìn)行的,實(shí)際應(yīng)用效果有待進(jìn)一步考證。
參考文獻(xiàn)
[1] 要煥年, 曹梅月. 電力系統(tǒng)諧振接地[M]. 北京:中國電力出版社, 2009.
[2] 賀家李, 宋從矩. 電力系統(tǒng)繼電保護(hù)原理[M]. 北京:中國電力出版社, 1994.
[3] 徐偉宗. 采樣頻率對行波測距影響的仿真分析[J]. 電力系統(tǒng)及其自動化學(xué)報(bào), 2014, 26(6):76-80.
[4] 易吉良. 基于S變換的電能質(zhì)量擾動分析[D]. 長沙:湖南大學(xué), 2010.
[5] 束洪春. 電力工程信號處理應(yīng)用[M]. 北京:科學(xué)出版社, 2009.
[6] CHU P C. The S transform for obtaining localized spectra[J]. Marine Technology Society Journal, 1995, 29(4):28-38.
[7] PINNEGAR C R, MANSINHA L. Time frequency localization with the Hartley Stransform[J]. Signal Processing, 2004, 84(12):2437-2442.
[8] 易吉良, 彭建春, 譚會生. 采用不完全S變換的電能質(zhì)量擾動檢測方法[J]. 高電壓技術(shù), 2009, 35(10):2562-2567.
[9] 李立, 易吉良, 朱建林. 采用改進(jìn)不完全S變換估計(jì)電能質(zhì)量擾動參數(shù)[J]. 電工技術(shù)學(xué)報(bào), 2011(6):187-193.

